官网介绍

Toy

设$\mathbf{X},\mathbf{Y}\in {\mathbf{R}}^{n\times d}$，假设其中$\mathbf{X}$是模型的输入，$\mathbf{Y}$是真实标签

默认参数

torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')
如果在模型训练中直接使用MSELoss，即

loss = torch.nn.MSELoss()
loss = loss(X, Y)
print(loss)
loss.backward()
print(X.grad)

则$loss=\frac{1}{n\times d}||X-Y|{|}^2$
$X.grad=\frac{\partial loss}{\partial X}=\frac{\partial \frac{1}{n\times d}||X-Y|{|}^2}{\partial X}=\frac{2}{n\times d}(\mathbf{X}-\mathbf{Y})$ ,范数求导参考¹

例如
$\mathbf{X}=\left[\begin{array}{cc}3& 1\\ 4& 2\\ 5& 3\end{array}\right],\mathbf{Y}=\left[\begin{array}{cc}2& 2\\ 1& 4\\ 6& 2\end{array}\right]\Rightarrow loss=\frac{1}{3\times 2}{\Vert \begin{array}{cc}3-2& 1-2\\ 4-1& 2-4\\ 5-6& 3-2\end{array}\Vert }^2=17/6=2.8333$
$X.grad=\frac{2}{3\times 2}\left[\begin{array}{cc}3-2& 1-2\\ 4-1& 2-4\\ 5-6& 3-2\end{array}\right]=\frac{1}{3}\left[\begin{array}{cc}1& -1\\ 3& -2\\ -1& -1\end{array}\right]$
代码实现

import torch
X = torch.tensor([[3, 1], [4, 2], [5, 3]], dtype=torch.float, requires_grad=True)
Y = torch.tensor([[2, 2], [1, 4], [6, 2]], dtype=torch.float)
loss = torch.nn.MSELoss()
loss = loss(X, Y)
loss.backward()
print(loss)
# tensor(2.8333, grad_fn=<MseLossBackward0>)
print(X.grad)
#tensor([[ 0.3333, -0.3333],
#        [ 1.0000, -0.6667],
#        [-0.3333,  0.3333]])

定制参数

torch.nn.MSELoss(reduction='sum')
如果在模型训练中使用MSELoss(reduction='sum')，即

loss = torch.nn.MSELoss(reduction='sum')
loss = loss(X, Y)
print(loss)
loss.backward()
print(X.grad)

则$loss=||X-Y|{|}^2$
$X.grad=\frac{\partial loss}{\partial X}=\frac{\partial ||X-Y|{|}^2}{\partial X}=2(\mathbf{X}-\mathbf{Y})$

例如
$\mathbf{X}=\left[\begin{array}{cc}3& 1\\ 4& 2\\ 5& 3\end{array}\right],\mathbf{Y}=\left[\begin{array}{cc}2& 2\\ 1& 4\\ 6& 2\end{array}\right]\Rightarrow loss={\Vert \begin{array}{cc}3-2& 1-2\\ 4-1& 2-4\\ 5-6& 3-2\end{array}\Vert }^2=17$
$X.grad=2\left[\begin{array}{cc}3-2& 1-2\\ 4-1& 2-4\\ 5-6& 3-2\end{array}\right]=\left[\begin{array}{cc}2& -2\\ 6& -4\\ -2& -2\end{array}\right]$
代码实现

import torch
X = torch.tensor([[3, 1], [4, 2], [5, 3]], dtype=torch.float, requires_grad=True)
Y = torch.tensor([[2, 2], [1, 4], [6, 2]], dtype=torch.float)
loss = torch.nn.MSELoss(reduction='sum')
loss = loss(X, Y)
loss.backward()
print(loss)
# tensor(17., grad_fn=<MseLossBackward0>)
print(X.grad)
#tensor([[ 2., -2.],
#        [ 6., -4.],
#        [-2.,  2.]])

预测问题-线性回归

为了解释线性回归，我们举一个实际的例子²： 我们希望根据房屋的面积（平方英尺）和房龄（年）来估算房屋价格（美元）。
使用$n$来表示数据集中的样本数。对索引为$i$的样本，其输入表示为${\mathbf{x}}^{(i)}=[x_1^{(i)},x_2^{(i)}{]}^{\top }$，其对应的标签是$y^{(i)}$。

线性假设是指目标（房屋价格）可以表示为特征（面积和房龄）的加权和，如下面的式子：

$$\mathrm{price}=w_{\mathrm{area}}\cdot \mathrm{area}+w_{\mathrm{age}}\cdot \mathrm{age}+b.$$

给定一个数据集，我们的目标是寻找模型的权重$\mathbf{w}=[w_1,w_2]$和偏置$b$，使得根据模型做出的预测大体符合数据里的真实价格。

这里为了手算简单，我们使用的数据集有6个样本$\mathbf{X}\in {\mathbf{R}}^{6\times 2},\mathbf{y}\in {\mathbf{R}}^6$。
即$\mathbf{X}=\left[\begin{array}{cc}1& 2\\ 4& 2\\ 8& 1\\ 0& 1\\ 3& 8\\ 1& 3\end{array}\right]，\mathbf{y}=\left[\begin{array}{c}1\\ 6\\ 2\\ 7\\ 1\\ 3\end{array}\right]$。

麻雀虽小五脏俱全，我们将这6个样本分批训练，即batch_size = 3，同时为了复现上述的线性假设，我们使用nn.Linear(2, 1)，即含有三个可学习的参数，分别是模型的权重$\mathbf{w}=[w_1,w_2]$和偏置$b$，我们初始化模型参数为${\mathbf{w}}_0=[1,2]$和偏置$b_0$=0。这里也使用常用的优化算法stochastic gradient descent，即torch.optim.SGD()。进一步方便手算，我们使用的学习率lr = 0.5。训练之前的代码如下

import numpy as np
import torch
from torch.utils import data

# 为了手算理解内部计算过程，我们手动随便输入数据组成数据集
# 这里的数据集有6个数据样本，每个样本有两个特征
features = torch.tensor([[1, 2], [4, 2], [8, 1], [0, 1], [3, 8], [1, 3]], dtype=torch.float)
labels = torch.tensor([[1], [6], [2], [7], [1], [3]], dtype=torch.float)
# print(features, '\n', labels)

def load_array(data_arrays, batch_size, is_train=True): 
    """构造一个PyTorch数据迭代器"""
    # 布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

# 因为数据集有6个样本，所以这里批大小可以是3，为了理解而服务
batch_size = 3
data_iter = load_array((features, labels), batch_size)

# nn是神经网络的缩写
from torch import nn
# y = x_1*w_1 + x_2*w_2 + b
net = nn.Sequential(nn.Linear(2, 1))

# 手动初始化两个权重和偏置
net[0].weight.data = torch.tensor([[1, 2]], dtype=torch.float)
net[0].bias.data.fill_(0)
# print(net[0].weight.data, '\n', net[0].bias.data)

# 这里使用均方误差，即2范数的平方和，在训练迭代过程中要除以batch_size
loss=torch.nn.MSELoss(reduction='sum')

trainer = torch.optim.SGD(net.parameters(), lr=0.5)

训练过程：
在每个迭代周期里，我们将完整遍历一次数据集（train_data），不停地从中获取一个小批量的输入和相应的标签。对于每一个小批量，我们会进行以下步骤:

• 通过调用net(X)生成预测并计算损失l（前向传播）。
• 通过进行反向传播来计算梯度。
• 通过调用优化器来更新模型参数。

为了更好的衡量训练效果，我们计算每个迭代周期后的损失，并打印它来监控训练过程。

# 训练周期为3
num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
#        print('X: ', X, ',y :', y)
#        print(len(y))
		# len(y)是批量大小，这里是为了让学习率与批量大小解耦 
        l = loss(net(X) ,y)/len(y)
#        print('l:', l)
        trainer.zero_grad()
        l.backward()
#        print('net[0].weight.data: ',net[0].weight.data,'\nnet[0].bias.data: ', net[0].bias.data)
#        print('w.grad: ', net[0].weight.grad, '\nb.grad: ', net[0].bias.grad)
        trainer.step()
        
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

每个训练周期中，因为$batch\_size=3$，所以一共有$n/batch\_size=6/3$个批次，假设$epoch0$的第一批抽取的3个样本组成的输入特征$\mathbf{X}\in {\mathbf{R}}^{3\times 2}$和标签$\mathbf{y}\in {\mathbf{R}}^3$，分别(这里因为每批次的样本是从数据集中随机抽取的，所以具体运行因人而异)是$\mathbf{X}=\left[\begin{array}{cc}1& 3\\ 4& 2\\ 1& 2\end{array}\right],\mathbf{y}=\left[\begin{array}{c}3\\ 6\\ 1\end{array}\right]$，则$loss=\frac{1}{|batch\_size|}||X\mathbf{w}+\mathbf{b}-y|{|}^2=\frac{1}{3}{\Vert \begin{array}{c}\left[\begin{array}{cc}1& 3\\ 4& 2\\ 1& 2\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]-\left[\begin{array}{c}3\\ 6\\ 1\end{array}\right]\end{array}\Vert }^2=12$，$\mathbf{w}.grad=\frac{\partial loss}{\partial \mathbf{w}}=\frac{\partial \frac{1}{|batch\_size|}||X\mathbf{w}+\mathbf{b}-y|{|}^2}{\partial \mathbf{w}}=\frac{2}{|batch\_size|}{X}^T(X\mathbf{w}+\mathbf{b}-y)=\frac{2}{3}{\left[\begin{array}{cc}1& 3\\ 4& 2\\ 1& 2\end{array}\right]}^T(\left[\begin{array}{cc}1& 3\\ 4& 2\\ 1& 2\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]-\left[\begin{array}{c}3\\ 6\\ 1\end{array}\right])=\left[\begin{array}{c}\frac{32}{3}\\ 16\end{array}\right]$(这里偏置$\mathbf{b}$使用了torch.tensor的广播机制³)。

值得注意的是$loss=\frac{1}{|batch\_size|}||X\mathbf{w}+\mathbf{b}-y|{|}^2$，这种形式是为了处理像这种多个维度的向量\矩阵，那么对于标量$\mathbf{b}$而言，$loss=\frac{1}{|batch\_size|}||X\mathbf{w}+\mathbf{b}-y|{|}^2=\frac{1}{|batch\_size|}{\sum }_{i=1}^{|batch\_size|}(x_1{w}_1+x_2{w}_2+\mathbf{b}-y{)}^2=\frac{1}{3}[(1\ast 1+3\ast 2+0-3{)}^2+(4\ast 1+2\ast 2+0-6{)}^2+(1\ast 1+2\ast 2+0-1{)}^2]=12$，所以$\mathbf{b}.grad=\frac{\partial loss}{\partial \mathbf{b}}=\frac{\partial \frac{1}{|batch\_size|}{\sum }_{i=1}^{|batch\_size|}(x_1{w}_1+x_2{w}_2+\mathbf{b}-y{)}^2}{\partial \mathbf{b}}=\frac{2}{|batch\_size|}{\sum }_{i=1}^{|batch\_size|}(x_1{w}_1+x_2{w}_2+\mathbf{b}-y)=\frac{2}{3}[(1\ast 1+3\ast 2+0-3)+(4\ast 1+2\ast 2+0-6)+(1\ast 1+2\ast 2+0-1)]=\frac{20}{3}=6.6667$。

运行截图：

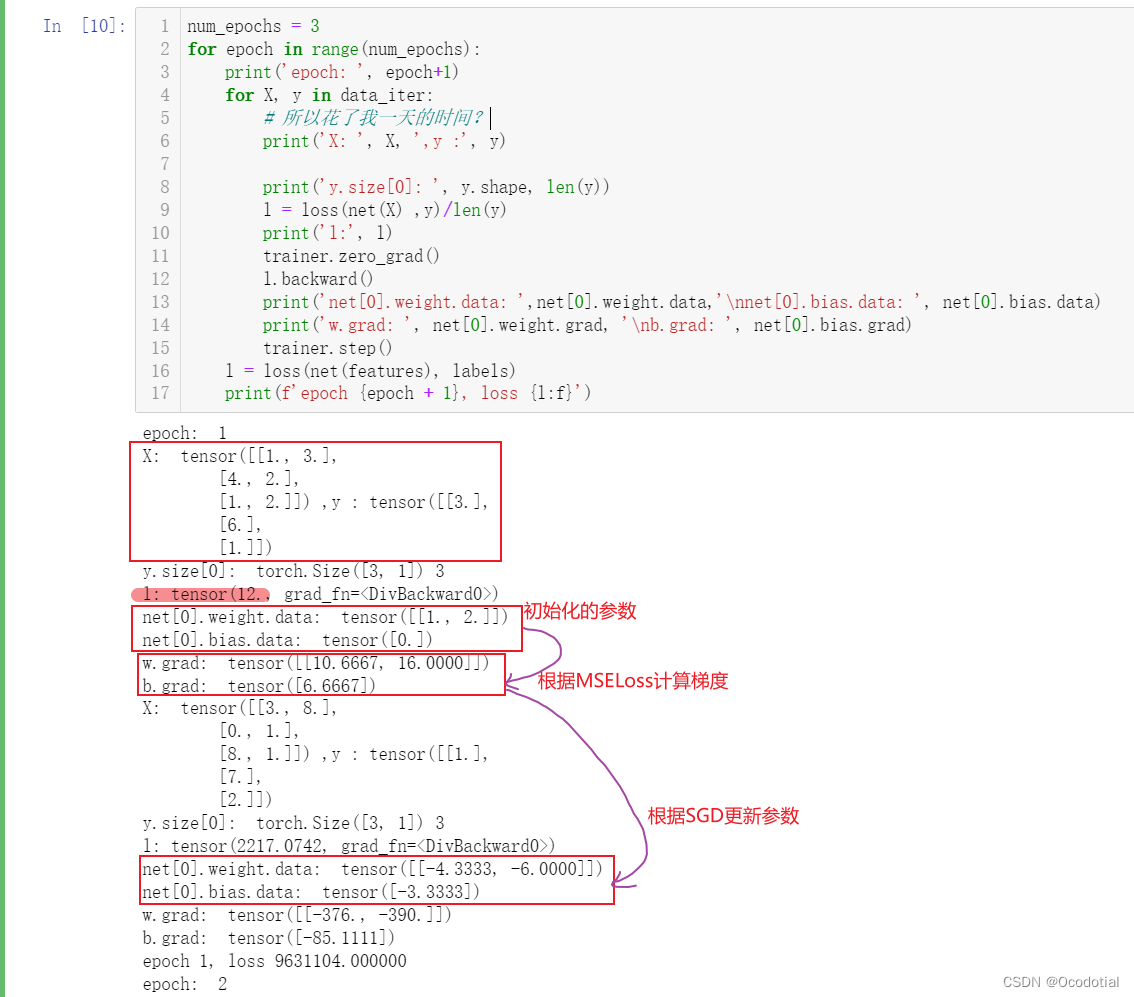
同时可学习的参数$\mathbf{w}$和$\mathbf{b}$通过SGD得到更新，即
${\mathbf{w}}_1={\mathbf{w}}_0-\eta \frac{\partial loss}{\partial \mathbf{w}}={\mathbf{w}}_0-\eta \mathbf{w}.grad=\left[\begin{array}{c}1\\ 2\end{array}\right]-0.5\ast \left[\begin{array}{c}10.6667\\ 16\end{array}\right]=\left[\begin{array}{c}-4.3333\\ -6\end{array}\right]$和偏置${\mathbf{b}}_1={\mathbf{b}}_0-\eta \frac{\partial loss}{\partial \mathbf{b}}={\mathbf{b}}_0-\eta \mathbf{b}.grad=0-0.5\ast 6.6667=-3.3333$。后面的更新类似迭代即可。

---

1. http://matrixcookbook.com ↩︎

2. https://zh.d2l.ai/chapter_linear-networks/linear-regression-concise.html ↩︎

3. https://zh.d2l.ai/chapter_linear-networks/linear-regression-scratch.html ↩︎