1. 题目

2. 解题思路

第一个丑数是 $1$，由于丑数的质因子只包含 $2、3、5$，所以后面的丑数肯定是前面的丑数分别乘以 $2、3、5$ 后得到的数字。

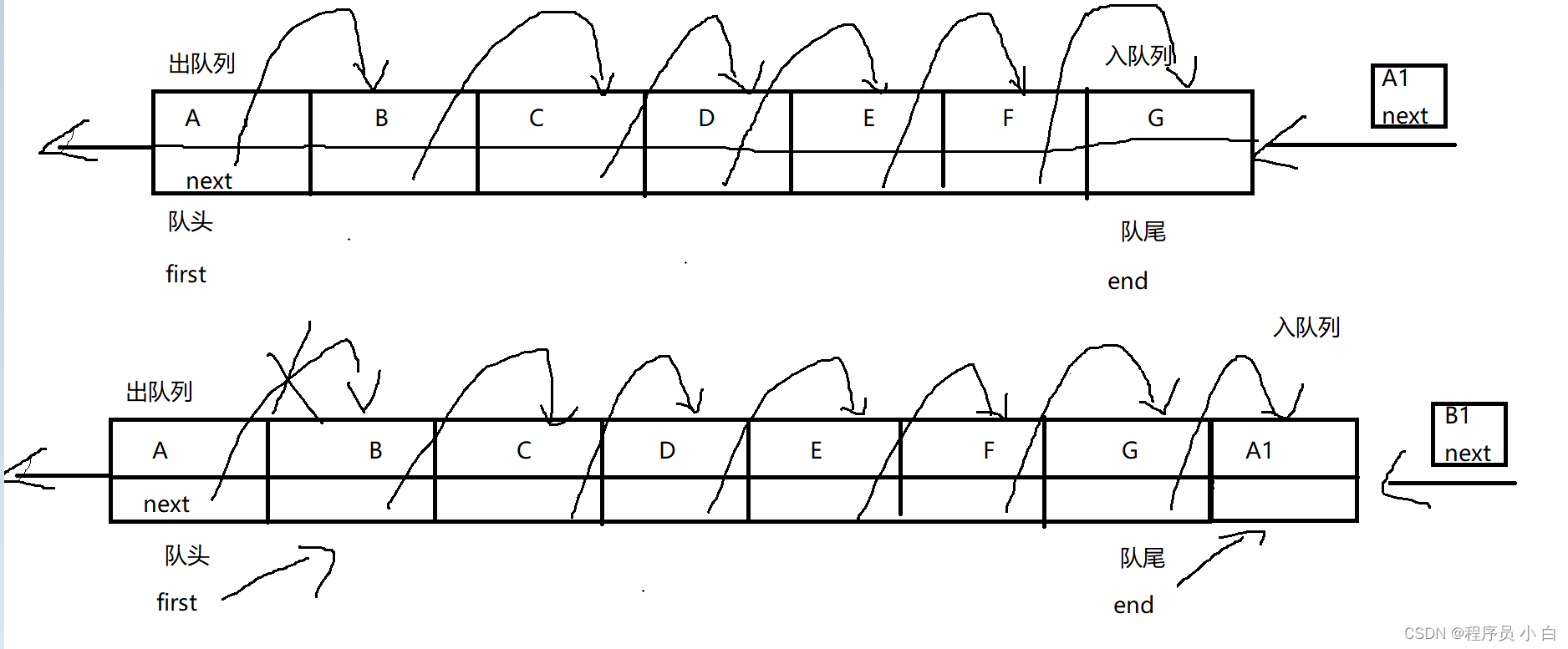
这样，我们维护三个队列，factors_two、factors_three、factors_five，分别代表前面的丑数乘以 $2、3、5$ 之后得到的数字序列。然后，每一次，我们只需要从这三个队列头部取一个最小的元素作为下一个丑数即可。当三个队列有一个为空的时候，我们就取出下一个丑数，分别填充到三个队列中去。

上面的方法可以进一步优化，其实每一次比较的时候我们只用到了三个队列头部的元素，而三个队列头部的元素又分别是某一个丑数乘以 $2、3、5$ 后得到的数字，所以，我们只需要分别记录三个队列头部元素对应的丑数即可。

时间复杂度为 $O(n)$，空间复杂度为 $O(n)$。

3. 代码实现

class Solution {
public:
    int nthUglyNumber(int n) {
        vector<unsigned int> uglyNumbers = {1};
        uglyNumbers.reserve(n+1);
        queue<unsigned int> factors_two;
        queue<unsigned int> factors_three;
        queue<unsigned int> factors_five;
        int idx = 0;
        while (uglyNumbers.size() < n) {
            if (factors_two.empty() || factors_three.empty() || factors_five.empty()) {
                factors_two.push(uglyNumbers[idx] * 2);
                factors_three.push(uglyNumbers[idx] * 3);
                factors_five.push(uglyNumbers[idx++] * 5);
            }
            int min_num = min(min(factors_two.front(), factors_three.front()), factors_five.front());
            uglyNumbers.push_back(min_num);
            if (min_num == factors_two.front()) {
                factors_two.pop();
            } 
            if (min_num == factors_three.front()) { 
                factors_three.pop();
            } 
            if (min_num == factors_five.front()) {
                factors_five.pop();
            }
        }
        return uglyNumbers[n-1];
    }
};

优化后的代码如下：

class Solution {
public:
    int nthUglyNumber(int n) {
        vector<unsigned int> uglyNumbers = {1};
        uglyNumbers.reserve(n+1);
        int factors_two = 0;
        int factors_three = 0;
        int factors_five = 0;
        while (uglyNumbers.size() < n) {
            unsigned int p2 = uglyNumbers[factors_two] * 2;
            unsigned int p3 = uglyNumbers[factors_three] * 3;
            unsigned int p5 = uglyNumbers[factors_five] * 5;
            unsigned int min_num = min(min(p2, p3), p5);
            uglyNumbers.push_back(min_num);
            if (min_num == p2) {
                ++factors_two;
            } 
            if (min_num == p3) { 
                ++factors_three;
            } 
            if (min_num == p5) {
                ++factors_five;
            }
        }
        return uglyNumbers[n-1];
    }
};