sigmoid和softmax

sigmoid和softmax都是分类函数，他们的区别如下

sigmoid函数

Sigmoid =多标签分类问题=多个正确答案=非独占输出（例如胸部X光检查、住院）。构建分类器，解决有多个正确答案的问题时，用Sigmoid函数分别处理各个原始输出值。
Sigmoid函数是一种logistic函数，它将任意的值转换到 $[0,1]$之间，如图1所示，函数表达式为： $$Sigmoid(x)=\frac{1}{1+e^{-x}}$$
它的导函数为：
$$Sigmoi{d}^{\prime }(x)=Sigmoid(x)\cdot (1-Sigmoid(x))$$

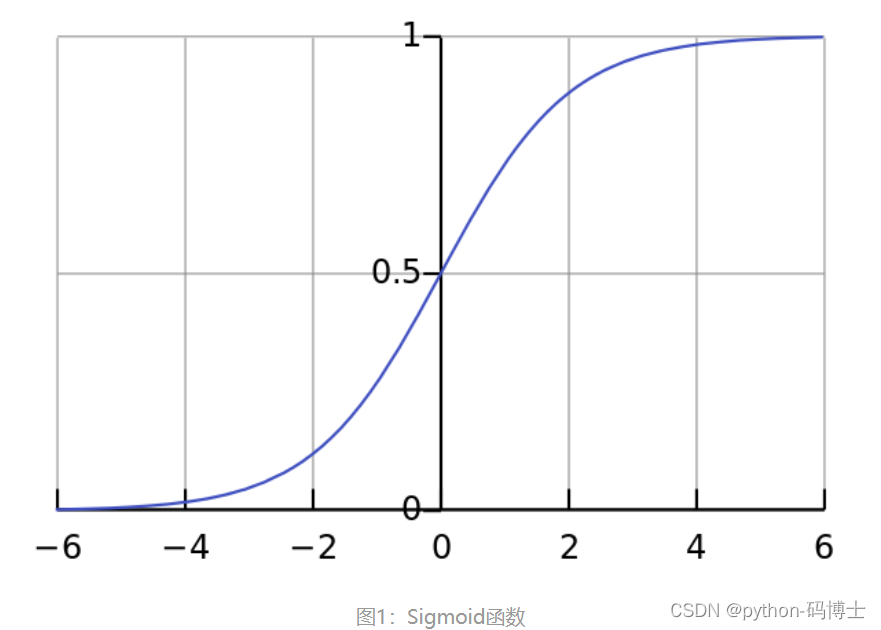
优点：1. Sigmoid函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。2. 连续函数，便于求导。
缺点：1. 最明显的就是饱和性，从上图也不难看出其两侧导数逐渐趋近于0，容易造成梯度消失。2.激活函数的偏移现象。Sigmoid函数的输出值均大于0，使得输出不是0的均值，这会导致后一层的神经元将得到上一层非0均值的信号作为输入，这会对梯度产生影响。 3. 计算复杂度高，因为Sigmoid函数是指数形式。

softmax函数

Softmax =多类别分类问题=只有一个正确答案=互斥输出（例如手写数字，鸢尾花）。构建分类器，解决只有唯一正确答案的问题时，用Softmax函数处理各个原始输出值。Softmax函数的分母综合了原始输出值的所有因素，这意味着，Softmax函数得到的不同概率之间相互关联。
Softmax函数，又称归一化指数函数，函数表达式为：
$$Softmax(x)=\frac{e^{x_i}}{{\sum }_{j=1}^n{e}^{x_j}}$$

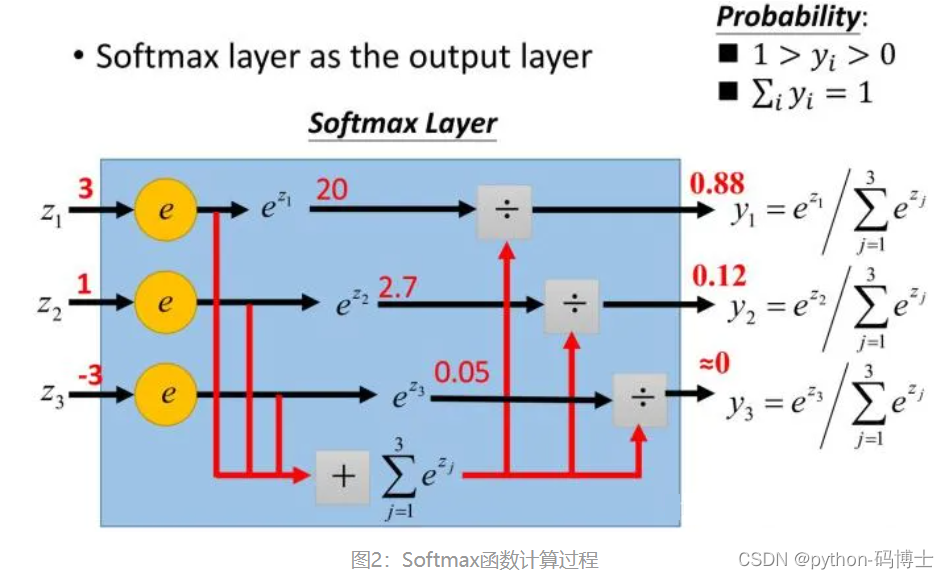
Softmax函数是二分类函数Sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。
如图2所示，Softmax直白来说就是将原来输出是3,1,-3通过Softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标。
Softmax可以由三个不同的角度来解释。从不同角度来看softmax函数，可以对其应用场景有更深刻的理解：

• softmax可以当作arg max的一种平滑近似，与arg max操作中暴力地选出一个最大值（产生一个one-hot向量）不同，softmax将这种输出作了一定的平滑，即将one-hot输出中最大值对应的1按输入元素值的大小分配给其他位置。
• softmax将输入向量归一化映射到一个类别概率分布，即 个类别上的概率分布（前文也有提到）。这也是为什么在深度学习中常常将softmax作为MLP的最后一层，并配合以交叉熵损失函数（对分布间差异的一种度量）。
• 从概率图模型的角度来看，softmax的这种形式可以理解为一个概率无向图上的联合概率。因此你会发现，条件最大熵模型与softmax回归模型实际上是一致的，诸如这样的例子还有很多。由于概率图模型很大程度上借用了一些热力学系统的理论，因此也可以从物理系统的角度赋予softmax一定的内涵。

总结

1.如果模型输出为非互斥类别，且可以同时选择多个类别，则采用Sigmoid函数计算该网络的原始输出值。
2.如果模型输出为互斥类别，且只能选择一个类别，则采用Softmax函数计算该网络的原始输出值。
3.Sigmoid函数可以用来解决多标签问题，Softmax函数用来解决单标签问题。
4.对于某个分类场景，当Softmax函数能用时，Sigmoid函数一定可以用。