通过前几期的学习，我们已经学会了排队论的基本概念、生灭过程和Poisson过程，等待制排队模型、混合制排队模型、其他排队模型以及排队系统优的定义与相关求解方法。在实际工作中，我们能发现排队论在经济管理中有着许多应用，本期小编选择了其中一些典型例子，包括等待制排队模型、混合制排队模型以及M/M/1模型中的最优服务率问题，进行详细讲解。

一些常见的等待制模型包括：M/M/1单服务台等待制模型：一个服务台，到达和服务时间都是指数分布；M/M/s多服务台模型：多个服务台，到达和服务时间都是指数分布。这些模型可以用于计算系统的性能指标，如平均等待时间、系统繁忙度、平均服务时间等。通过分析这些指标，可以优化系统，提高效率，降低等待时间，从而提升顾客体验。

1、问题描述

工厂中只有一个服务台，工件按泊松流到达服务台，平均间隔时间为10分钟，假设对每一工件的服务所需时间服从负指数分布，平均服务时间8分钟。求:

（1）工件在系统内等待服务的平均数和工件在系统内平均逗留时间；

（2）若要求在90%的把握使工件在系统内的逗留时间不超过30分钟，则工件的平均服务时间最多是多少；

（3）若每一工件的服务分两段，每段所需时间都服从负指数分布，平均都为4分钟，在这种情况下，工件在系统内的平均数是多少?

2、问题解析

由题目可知该问题是M/M/1单服务台等待制模型，其中到达率λ=1/10，服务率μ=1/8，服务强度ρ=0.8。

（1）工件在系统内等待服务的平均数即排队长

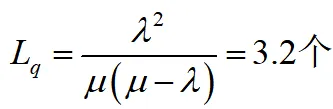
工件在系统中的平均逗留时间

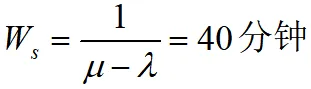
（2）工件在系统中逗留时间不超过30分钟的概率

得

故工件得平均服务时间最多为5.6分钟。

（3）此时模型变为M/M/2等待制排队模型，其中s=2服务率μ1=μ2=0.25=μ，服务强度ρ=λ/μ=0.4，ρs=λ/2μ=0.2，则平均排队长

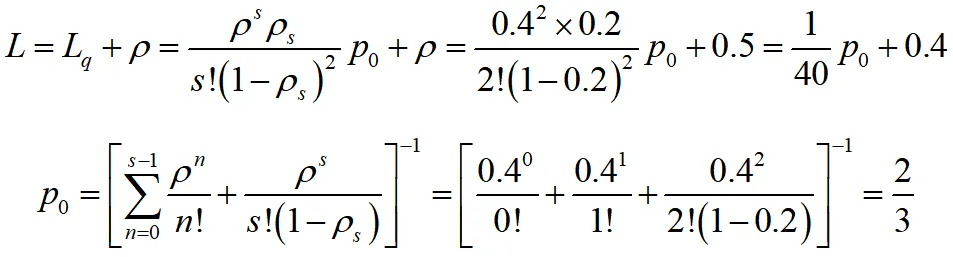
故系统中的工件数为

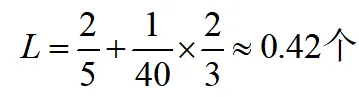
小结

单服务台模型与多服务台模型的区别：

（1）服务台数量：

单服务台模型：只有一个服务台为顾客提供服务

多服务台模型：包含多个服务台，每个服务台都可以同时为顾客提供服务

（2）服务率：

单服务台模型：取决于单个服务台的处理能力

多服务台模型： 由所有服务台的总体处理能力决定，取决于每个服务台的速率以及服务台的数量

在现实生活中，很多服务系统都应用混合制排队模型，当顾客到达时，服务台不空就排队，若排队位置已满就离去，如果系统的最大容量为K ，对于单服务台的情形，排队等待的顾客最多为K-1，在某时刻，顾客到达时，如系统中已有K个顾客，那么这个顾客就被拒绝进入系统。

1、问题描述

单人理发馆有 6 个椅子接待人们排队等待理发。当 6个椅子都坐满时，后来到的顾客不进店就离开。顾客平均到达率为 3人/小时，理发平均每人15 分钟。

（1）求某顾客到达理发馆就能理发的概率；

（2）求需要等待的顾客数的期望值；

（3）求有效到达率；

（4）求顾客在理发馆内逗留的期望时间；

（5）在可能到来的顾客中不等待就离开的概率。

2、问题解析

根据题目可知，该问题是该模型为K=7的M/M/1/K的模型，可得到达率λ=3人/小时，服务率μ=4人/小时，服务强度ρ=λ/μ=0.75

（1）到达理发馆就能理发情形相当于理发馆内没有顾客，所求概率

（2）需要等待的顾客数的期望值，就是平均排队长

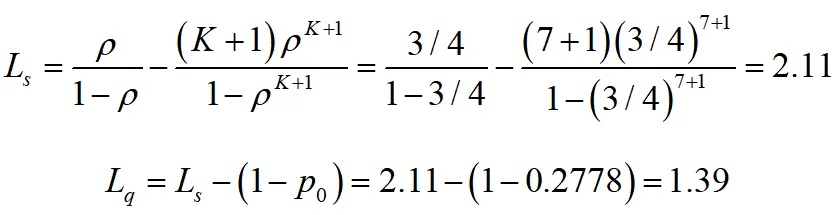
（3）顾客的有效到达率为

（4）顾客在理发馆内逗留的期望时间就是平均逗留时间

（5）顾客不等待就离开的概率，即系统拒绝率也是系统满员率

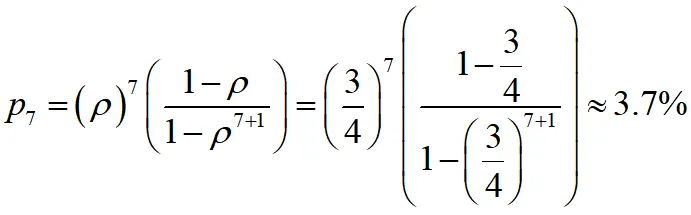
这也是理发馆的损失率为3.7%。

总结

等待制模型与混合制模型的区别

等待制模型：顾客源无限，系统空间无限，允许无限排队，当顾客到达时所有的服务台均被占用，顾客就排队等待，直到接受完服务才离去。

混合制模型：顾客源无限，系统空间有限，不允许无限排队，混合制模型既有等待又有损失，在限度以内就排队等待，超过一定限度就离去。

在M/M/1队列模型中，最优服务率通常是指能够使系统达到某种性能指标的最佳服务率。这个性能指标可能是最小的平均等待时间、最小的系统繁忙度或最大的系统通过率。具体来说，M/M/1模型的最优服务率是在给定到达率的情况下，通过调整服务率μ来实现某个优化目标。

1、问题描述

某公司医务室为职工检查身体，职工的到达服从泊松分布，每小时平均到达50人，若职工不能按时体检，造成的损失为每小时每人平均60元。体检所花时间服从指数分布负指数分布，平均每小时服务率为μ，每人的体检费为30元，试确定使公司总支出最少的参数μ。

2、问题解析

该问题求解公司总支出最少的参数μ，即平均服务率的最优值，根据题意可知，该排队模型为M/M/1模型，那么单位时间服务成本与顾客在系统逗留费用之和

式中Cs为当μ=1时服务机构单位时间的费用；Cw为每个顾客在系统停留单位时间的费用。则代入模型的平均队长公式可得

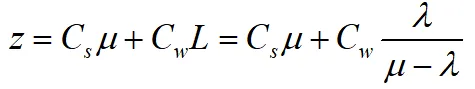
对μ进行求导，并令导数为零，得

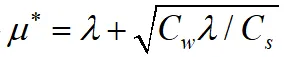
故

注意

       M/M/1模型是相对简单的排队模型，因此最优服务率的解通常可以通过解析方法找到，对于更复杂的排队模型，可能需要使用数值方法进行求解。

       以上就是本期排队论例题讲解的全部内容啦，通过对这一期的学习，相信大家一定能够加深对排队论的理解，进而在生活实践中学会应用！

作者 | 林鑫 马书良

责编 | 王一静

审核 | 徐小峰