目录
基础知识
例子
推荐
A Visual Exploration of Gaussian Processes (distill.pub)
AB - Introduction to Gaussian Processes - Part I (bridg.land)
基础知识
高斯过程回归(Gaussian Process Regression) - 知乎 (zhihu.com)
高斯过程(Gaussian Process, GP)是随机过程之一,是一系列符合正态分布的随机变量在一指数集(index set)内的集合。
高斯过程回归(Gaussian Process Regression, GPR)是使用高斯过程(Gaussian Process, GP)先验对数据进行回归分析的非参数模型(non-parameteric model)。
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。
而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
RBF核,若两个特征在指数上(即维度上)越相邻,它们之间的协方差系数就越高,这两个特征特征就越相关;若两个特征特征相隔越远,协方差系数越小,越不相关,所以RBF核可以用来模拟连续变化输出序列。
A Visual Exploration of Gaussian Processes (distill.pub)
回归是指找到一个函数尽可能好的接近一组数据点。
高斯过程是一个概率过程方法,对预测函数提供置信度。
高斯过程并不局限于回归 — 它们还可以扩展到分类和聚类任务
边缘化可以理解为在高斯分布的一个维度上做累加,这也符合边缘分布的一般定义。条件作用也有个很好的几何表达——我们可以把它想象成在多元分布上切下一刀,从而获得一个维数更少的高斯分布。
贝叶斯推断的核心思想就是:在获得新的信息以后,更新当前的假设。
kimi:
高斯过程(Gaussian Process)是一种用于非参数贝叶斯推断的机器学习算法。在高斯过程中,"先验"(Prior)是指对从高斯过程生成的函数的预先期望或假设。
先验可以看作是我们关于问题的一些初始知识或假设,它指定了函数值在整个函数空间的分布情况。在高斯过程中,这个分布是一个多元高斯分布,其均值和协方差通过一些指定的函数来定义。
1.均值函数:通常,将均值函数设定为0(或其他常数),这意味着在没有任何观测的情况下,我们假设函数的所有可能值的期望是0。
2.协方差函数(或者说核函数):定义了数据点之间的相似度。给定两个输入,协方差函数的值体现了对应的两个函数值的相似程度。通常选择的核函数使得输入相近的点具有较高的协方差,而相距较远的点具有较小的协方差。
当我们收集到一些观测数据后,我们需要对先验进行更新以获得后验分布。这就是通过贝叶斯规则来实现的,后验分布代表了在给定观测数据情况下,函数的预期分布。在高斯过程中,这个分布是以观测数据为条件的高斯分布。
高斯过程的先验表示了我们对从高斯过程产生的随机函数的预先期望或假设,这是在收集到任何实际观测数据之前就设立的假设。后续的学习过程就是不断地调整和更新这些假设,使得模型的预测更加准确。
coze:
高斯过程的先验是指在没有接收到任何观察数据时,对函数空间中可能的值进行的假设或预测。这通常包括两个部分:一个均值函数(mean function)和一个协方差函数(covariance function),这两者共同定义了函数在所有可能的输入集合中可能的输出值的分布。
-
均值函数:这个函数通常被定义为0,或者一些基于实际问题的初始预期值。也就是说,如果我们完全没有关于接收到的输入的任何有用信息,那么均值函数给出的就是我们对函数输出的预测。
-
协方差函数:也被称为核函数(Kernel function),它定义了输入值之间的相互依赖关系。基于协方差函数,我们可以知道对于一个给定输入以及其相对位置,期望输出值可能的变化性越大还是越小。
1.7. 高斯过程 - sklearn (scikitlearn.com.cn)
高斯过程 (GP) 是一种常用的监督学习方法,旨在解决回归问题和概率分类问题。
高斯过程模型的优点如下:
* 预测内插了观察结果(至少对于正则核)。
* 预测结果是概率形式的(高斯形式的)。这样的话,人们可以计算得到经验置信区间并且据此来判断是否需要修改(在线拟合,自适应)在一些区域的预测值。
* 通用性: 可以指定不同的:内核(kernels)。虽然该函数提供了常用的内核,但是也可以指定自定义内核。
高斯过程模型的缺点包括: * 它们不稀疏,例如,模型通常使用整个样本/特征信息来进行预测。 * 高维空间模型会失效,高维也就是指特征的数量超过几十个。
kimi.ai描述:
在统计学和概率论中,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性。似然函数是概率密度函数(probability density function, PDF)或概率质量函数(probability mass function, PMF)的泛化,用于参数估计和模型选择。
似然函数的定义
似然函数 \( L \) 通常表示为 \( L(\theta | x) \),其中:
- \( \theta \) 是模型参数,
- \( x \) 是观测数据。
似然函数的应用
1. **参数估计**:似然函数用于点估计,如最大似然估计(MLE)。在最大似然估计中,选择参数 \( \theta \) 的值使得观测数据的似然性最大。
2. **模型选择**:似然比检验(Likelihood Ratio Test, LRT)用于比较两个模型的拟合优度,通过比较它们的似然函数值来决定哪个模型更适合数据。
3. **贝叶斯统计**:在贝叶斯框架下,似然函数与先验概率结合,通过贝叶斯定理计算后验概率。
与概率的区别
似然函数与概率函数不同,主要区别在于:
- 概率函数 \( P(x | \theta) \) 描述在给定参数 \( \theta \) 下,观测 \( x \) 发生的概率。它是随机事件 \( x \) 的概率度量。
- 似然函数 \( L(\theta | x) \) 是在观测 \( x \) 已知的情况下,参数 \( \theta \) 的函数。它不是概率,而是一种衡量参数 \( \theta \) 相对于观测数据 \( x \) 的“合适度”。
最大似然估计(MLE)
最大似然估计是一种常用的参数估计方法,它寻找能够使观测数据出现概率最大的参数值。数学上,最大似然估计可以通过求解以下优化问题得到:
\[
\hat{\theta}_{MLE} = \arg\max_{\theta} L(\theta | x)
\]
其中,\( \hat{\theta}_{MLE} \) 是最大似然估计值。
似然函数是统计学中的核心概念之一,它为基于观测数据推断模型参数提供了一种方法。
【理解】似然函数-CSDN博客
正态分布(高斯分布)学习笔记 - 知乎 (zhihu.com)
高斯过程样本与一般机器学习的样本区别在于,高斯过程中样本各特征之间存在相关关系,这种相关关系是通过协方差矩阵来体现的。
比如在一些时间序列模型里面,各个变量输出的时间序列在时间前后都会体现出一种相关性(比如平滑过渡等),这种模型输出就很适合使用高斯过程来模拟。
各个维度特征之间的协方差可以通过高斯过程核(kernel)来模拟。
核函数&径向基核函数 (Radial Basis Function)--RBF-CSDN博客
原来在二维空间中一个线性不可分的问题,映射到四维空间后,变成了线性可分的!因此这也形成了我们最初想解决线性不可分问题的基本思路——向高维空间转化,使其变得线性可分。而转化最关键的部分就在于找到x到y的映射方法。
这样一种函数K(w,x),接受低维空间的输入值,却能算出高维空间的内积值<w’,x’>。它被称作核函数(核,kernel),而且还不止一个,事实上,只要是满足了Mercer条件的函数(后面会具体写出),都可以作为核函数。
核函数的基本作用就是接受两个低维空间里的向量,能够计算出经过某个变换后在高维空间里的向量内积值。
径向基函数 (Radial Basis Function 简称 RBF), 就是某种沿径向对称的标量函数。 通常定义为空间中任一点x到某
一中心xc之间欧氏距离的单调函数 ,可记作 k(||x-xc||), 其作用往往是局部的 , 即当x远离xc时函数取值很小。
最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)^2) } 其中x_c为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。如果x和x_c很相近那么核函数值为1,如果x和x_c相差很大那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数(Radial Basis Function 简称RBF)。它能够把原始特征映射到无穷维。它能够把原始特征映射到无穷维。
高斯核函数能够比较x和z的相似度,并映射到0到1,回想logistic回归,sigmoid函数可以,因此还有sigmoid核函数等等。
高斯过程回归(Gaussian process regression)原理详解及python代码实战-CSDN博客
点积、叉积、内积、外积【汇总对比】-CSDN博客
空间中两个向量的内积是一个标量,通常用尖括号表示,在欧氏向量空间中内积是笛卡尔坐标的点积或标量积。
两个数字序列的相应条目的乘积之和。在欧几里得几何中,两个向量的笛卡尔坐标的点积被广泛使用。它通常被称为欧几里得空间的内积(或很少称为投影积),是内积的一种特殊情况,尽管它不是可以在欧几里得空间上定义的唯一内积。
内积,点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影。
叉积或向量积(有时是有向面积积,以强调其几何意义)是在三维有向欧几里得向量空间,并用符号x表示. 给定两个线性独立的向量 a和b,叉积a × b(读作“a cross b”)是一个垂直于a和b的向量,因此垂直于包含它们的平面。
外积,外积的运算结果是一个张量而不是一个标量。
AB - Introduction to Gaussian Processes - Part I (bridg.land)
高斯过程提供了丰富的建模能力和不确定性估计。
机器学习中的大多数现代技术倾向于通过参数化函数然后对这些参数进行建模(例如线性回归中的权重)来避免这种情况。然而,GP 是直接对函数进行建模的非参数模型。这带来了一个非常重要的好处:我们不仅可以对任何黑盒函数进行建模,还可以对我们的不确定性进行建模。
GP 背后的关键思想是可以使用无限维多元高斯分布对函数进行建模。换句话说,输入空间中的每个点都与一个随机变量相关联,并且这些变量的联合分布被建模为多元高斯分布。
详细对比深度神经网络和高斯过程_高斯混合模型和深度模型区别-CSDN博客
例子
高斯过程--GPyTorch回归教程-CSDN博客
Implementing a custom kernel in GPyTorch — GPyTorch 0.1.dev97+gf73fa7d documentation
Q:这里面是如何表示高斯噪声的,为什么可以这么表示?
# True function is sin(2*pi*x) with Gaussian noise train_y = torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * math.sqrt(0.04)
A:train_y 表示的是正弦函数 sin(2𝜋𝑥)的值,叠加上了高斯噪声(也称为正态噪声)。高斯噪声是一种具有正态分布(高斯分布)概率密度函数的随机变量,其密度函数呈对称的钟形曲线形状。
-
torch.randn(train_x.size()):这个函数生成一个与train_x形状相同的张量,其元素是从标准正态分布(均值为0,方差为1)中随机抽取的值。torch.randn是 PyTorch 中用于生成服从标准正态分布的随机数的函数。 -
math.sqrt(0.04):这个值是高斯噪声的标准差,它是噪声方差的平方根。在这个例子中,方差是 0.04,所以标准差是 0.2。 -
*:乘法操作符用于将每个从标准正态分布中抽取的随机数乘以噪声的标准差,从而得到具有指定方差的高斯噪声。
因此,torch.randn(train_x.size()) * math.sqrt(0.04) 表示的是生成一个与 train_x 形状相同的张量,其元素是从均值为0、方差为0.04的正态分布中抽取的随机数。这样得到的噪声被添加到正弦函数的值上,从而模拟实际观测数据中可能存在的随机波动或噪声。
这种噪声模型在实际应用中非常常见,因为它可以模拟许多自然和人造系统中的随机波动。例如,在测量数据时,测量设备可能会引入随机误差;在金融模型中,市场波动可以被视为具有正态分布的随机过程。通过在模型中加入高斯噪声,可以更准确地模拟这些现象,并使模型更能适应现实世界的数据。
- 所有参数梯度置零
- 调用模型,计算损失loss
- loss反向传播填充梯度
- 优化器优化
train()用于优化模型超参数eval()用于通过模型后验做预测
完整代码:
import math
import torch
import gpytorch
from matplotlib import pyplot as plt
# Training data is 100 points in [0,1] inclusive regularly spaced
train_x = torch.linspace(0, 1, 100)
# True function is sin(2*pi*x) with Gaussian noise
train_y = torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * math.sqrt(0.04)
# We will use the simplest form of GP model, exact inference
class ExactGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
# initialize likelihood and model
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = ExactGPModel(train_x, train_y, likelihood)
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
training_iter = 2 if smoke_test else 50
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.1) # Includes GaussianLikelihood parameters
# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
for i in range(training_iter):
# Zero gradients from previous iteration
optimizer.zero_grad()
# Output from model
output = model(train_x)
# Calc loss and backprop gradients
loss = -mll(output, train_y)
loss.backward()
print('Iter %d/%d - Loss: %.3f lengthscale: %.3f noise: %.3f' % (
i + 1, training_iter, loss.item(),
model.covar_module.base_kernel.lengthscale.item(),
model.likelihood.noise.item()
))
optimizer.step()
# f_preds = model(test_x)
# y_preds = likelihood(model(test_x))
#
# f_mean = f_preds.mean
# f_var = f_preds.variance
# f_covar = f_preds.covariance_matrix
# f_samples = f_preds.sample(sample_shape=torch.Size(1000,))
# Get into evaluation (predictive posterior) mode
model.eval()
likelihood.eval()
# Test points are regularly spaced along [0,1]
# Make predictions by feeding model through likelihood
with torch.no_grad(), gpytorch.settings.fast_pred_var():
test_x = torch.linspace(0, 1, 51)
observed_pred = likelihood(model(test_x))
with torch.no_grad():
# Initialize plot
f, ax = plt.subplots(1, 1, figsize=(4, 3))
# Get upper and lower confidence bounds
lower, upper = observed_pred.confidence_region()
# Plot training data as black stars
ax.plot(train_x.numpy(), train_y.numpy(), 'k*')
# Plot predictive means as blue line
ax.plot(test_x.numpy(), observed_pred.mean.numpy(), 'b')
# Shade between the lower and upper confidence bounds
ax.fill_between(test_x.numpy(), lower.numpy(), upper.numpy(), alpha=0.5)
ax.set_ylim([-3, 3])
ax.legend(['Observed Data', 'Mean', 'Confidence'])
plt.show()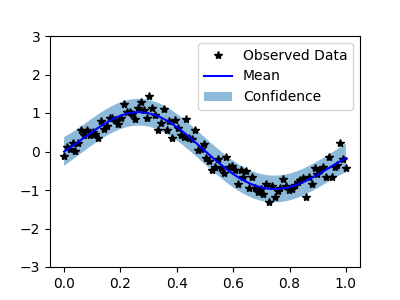
AB - Introduction to Gaussian Processes - Part I (bridg.land)