题意

平面上有一个点光源 $s$ 并以每秒 $1$ 单位长度的速度从点 $(a,sy)$ 移动到点 $(b,sy)$，其中 $sy<0$；在 $x$ 轴正方向上有 $n$ 不相交、不接触的挡板，第 $i$ 个档板挡住了 $x$ 轴上 $[l_i,r_i]$ 的部分。对于点 $(x,y)$，当它与 $s$ 的连线被某个挡板相交或接触时，我们说 $(x,y)$​ 在阴影中。

现在给定 $q$ 个平面上的点，求出这些点在 $s$ 移动过程中处于阴影内的总时间。

解法

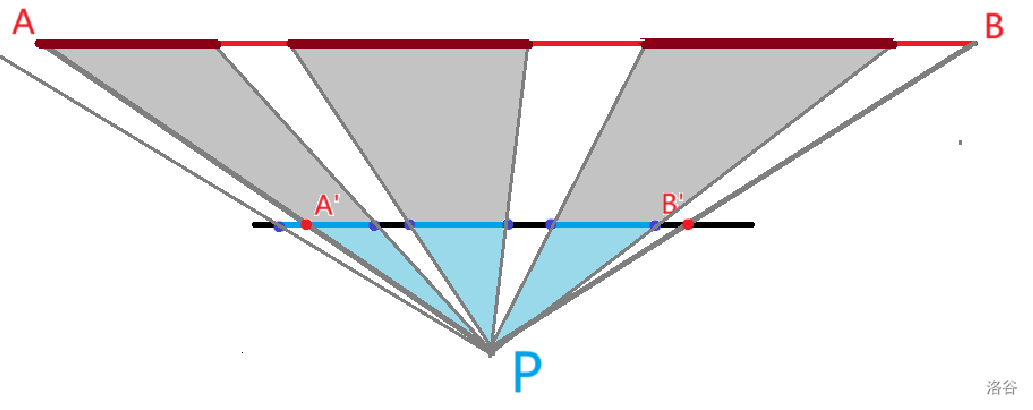
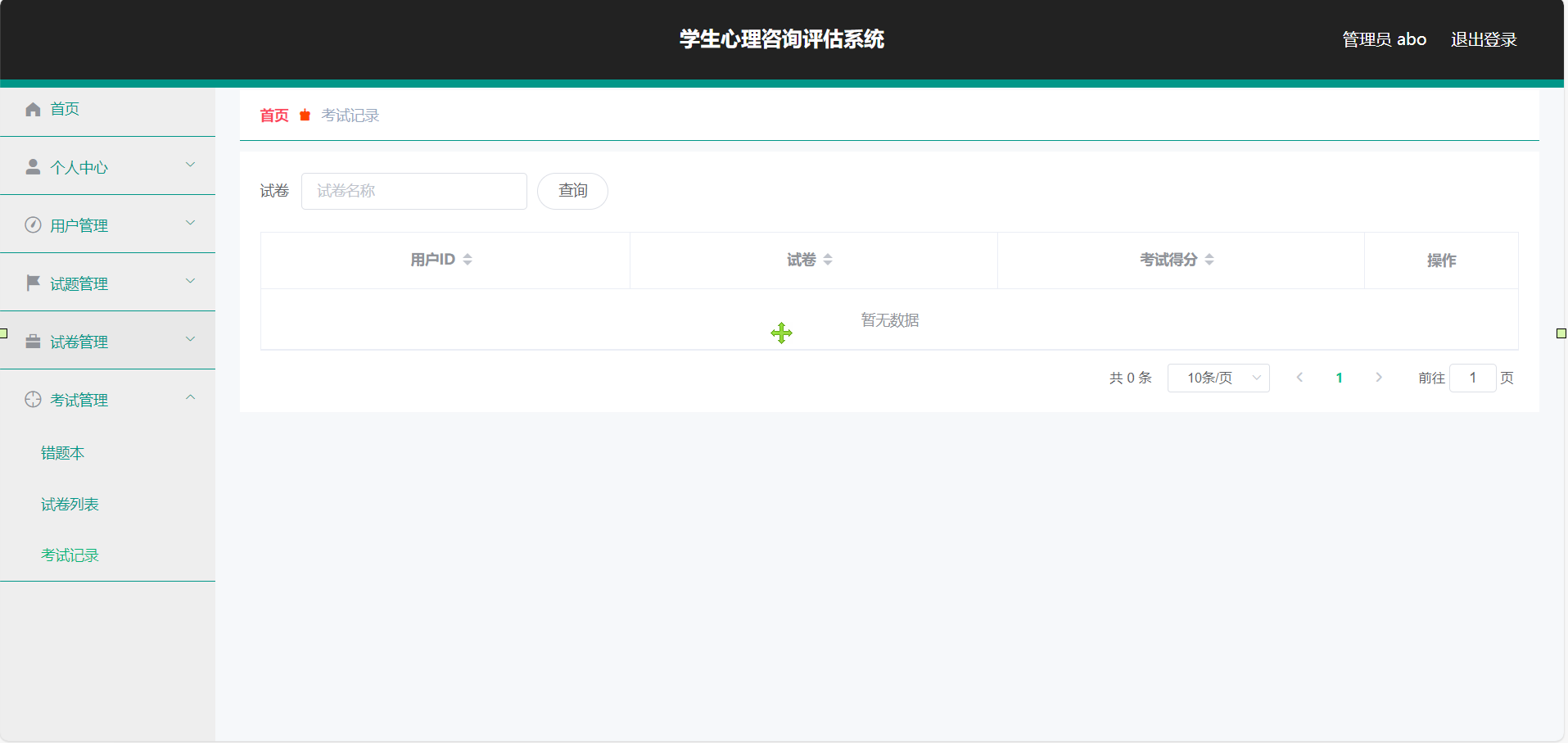
• 黑色部分为 $x$ 轴，蓝色部分为挡板，红色部分为 $s$ 的移动范围。

如图，对于一个点 $P$，连接点 $P$ 和 $A,B$ 交 $x$ 轴于两点 $A^{\prime },B^{\prime }$（灰色粗线）。我们求出 $[A^{\prime },B^{\prime }]$ 中挡板的占比后，就可以通过相似三角形（灰色、青色部分）求出 $[A,B]$ 上能让 $P$ 处于阴影中的总距离（深红色线）。我们将给定挡板按照 $x$ 坐标排序，两次二分求出 $A^{\prime }$ 和 $B^{\prime }$ 附近的挡板。预处理出挡板长度的前缀和统计这个点的贡献即可。具体见代码。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
const double eps = 1e-9;
struct Nodes { // 同时表示 A,B 两个点和挡板左右边界。
    double x,y;
    Nodes (double u = 0, double v = 0) {
        x = u, y = v;
    }
} X,Y,a[maxn],now;
int n; double sum[maxn];
int Q;
int main() {
    scanf("%lf%lf%lf%d",&X.y,&X.x,&Y.x,&n);
    n ++, Y.y = X.y;
    for (int i = 2;i <= n;i ++)
        scanf("%lf%lf",&a[i].x,&a[i].y),
        sum[i] = sum[i - 1] + (a[i].y - a[i].x);
    a[++ n] = Nodes{1e18,1e18}, sum[n] = sum[n - 1];
    scanf("%d",&Q);
    while (Q --) {
        scanf("%lf%lf",&now.x,&now.y);
        double k = now.y / (now.y - X.y); // 相似三角形
        double L = (X.x - now.x) * k + now.x, R = (Y.x - now.x) * k + now.x;
        if (L <= a[1].x || R >= a[n].y) { // 特判
            printf("%.6f\n",0);
            continue;
        }
        // 两边二分求左右的挡板
        int l = 1, r = n; 
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (a[mid].x <= L) l = mid;
            else r = mid - 1;
        }
        double ans = max(0.0,a[l].y - L) - sum[l];
        l = 1, r = n;
        while (l < r) {
            int mid = l + r >> 1;
            if (a[mid].y >= R) r = mid;
            else l = mid + 1;
        }
        ans += sum[r] - min(a[l].y - R, a[l].y - a[l].x);
        printf("%.7lf\n",ans * (Y.x - X.x) / (R - L)); 
    }
    return 0;
}