卷积计算

卷积是数学分析中的一种积分变换的方法，在图像处理中采用的是卷积的离散形式。这里需要说明的是，在卷积神经网络中，卷积层的实现方式实际上是数学中定义的互相关 （cross-correlation）运算，与数学分析中的卷积定义有所不同，这里跟其他框架和卷积神经网络的教程保持一致，都使用互相关运算作为卷积的定义，具体的计算过程如 图 所示。

互相关计算

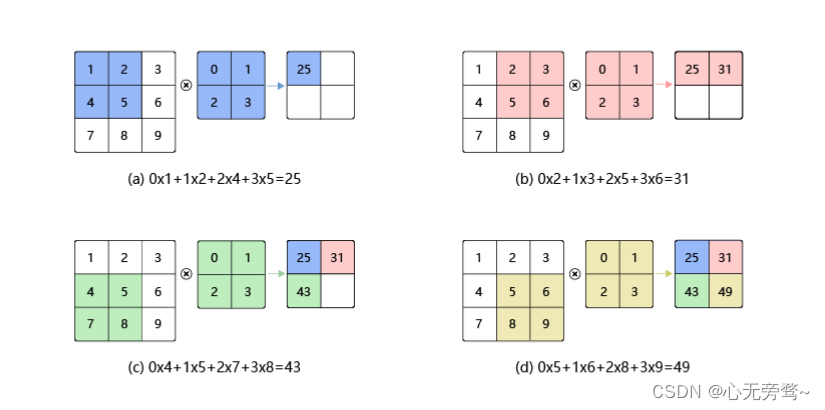
虽然卷积层得名于卷积（convolution） 运算，但我们通常在卷积层中使用更加直观的互相关（cross-correlation） 运算。在二维卷积层中，一个二维输入数组和一个二维核（kernel）数组通过互相关运算输出一个二维数组。我们用一个具体的例子来解释二维互相关运算的含义。如上图所示。

卷积核（kernel）也被叫做滤波器（filter），假设卷积核的高和宽分别为 $k_h$和$k_w$，则将称为$k_h\times k_w$卷积，比如$3\times 5$卷积，就是指卷积核的高为3，宽为5。

---

• 如上图（a）所示：左边的图大小是$3\times 3$，表示输入数据是一个维度为$3\times 3$的二维数组；中间的图大小是$2\times 2$，表示一个维度为$2\times 2$的二维数组，我们将这个二维数组称为卷积核。先将卷积核的左上角与输入数据的左上角(即：输入数据的(0,0)位置)对齐，把卷积核的每个元素跟其位置对其的输入数据中的元素相乘，再把卷积相加，得到卷积输出的第一个结果：

                  $0\times 1+1\times 2+2\times 4+3\times 5=25$  (a)

图中( b ), ( c ) ,(d )计算方法与上面雷同，相信聪明的大家不需要我再过多演示。

卷积核的计算过程可以用下面的数学公式表示，其中$a$代表输入图片，$b$代表输出特征图，$w$是卷积核参数，它们都是二维数组。

                      $b[i,j]=\sum _{u,v}a[i+u,j+v]\cdot w[u,v]$

举例说明，加入上图中卷积核大小是$2\times 2$，则$u$可以取0和1，$v$也可以取0和1，也就是说：

  $b[i,j]=a[i+0,j+0]\cdot w[0,0]+a[i+0,j+1]\cdot w[0,1]+a[i+1,j+0]\cdot w[1,0]+a[i+1,j+1]\cdot w[1,1]$

我们可以验证一下它的正确性，当$[i,j]$取不同值的时候，根据此公式计算的结果与上图的例子是否一致。

补充：
在卷积神经网络中，一个卷积算子除了上面描述的卷积过程之外，还包括加上偏置项的操作。例如假设偏置为1，则上面卷积计算的结果为：
$$0\times 1+1\times 2+2\times 4+3\times 5+1=26$$

$$0\times 2+1\times 3+2\times 5+3\times 6+1=32$$

$$0\times 4+1\times 5+2\times 7+3\times 8+1=44$$

$$0\times 5+1\times 6+2\times 8+3\times 9+1=50$$

练习

学完知识后，我们来做一道题进行下练习，帮助我们充分掌握卷积的运算。
题目：计算卷积中一共有多少次乘法和加法操作
输入数据形状是$[10,3,224,224]$,卷积核$k_h=k_w=3$,输出通道数为64，步幅$stride=1$，填充$p_h=p_w=1$。
则完成这样一个卷积，一共需要做多少次乘法和加法操作？

• 提示
  先看输出一个像素点需要做多少次乘法和加法操作，然后再计算总共需要的操作次数。

做题步骤：

1. 先考虑只有一个输入通道时候的二维卷积：
   假设输出是B，输入是A，先计算B的一个像素点，
   
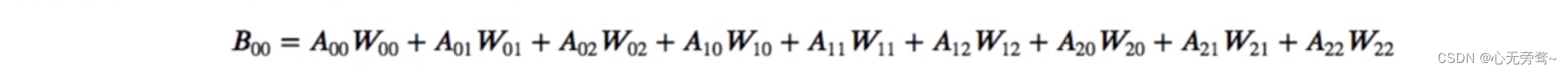
   其中，一共有9个乘法，8个加法操作。
   但是一般我们输入的图片都是RGB三通道的，所以我们需要计算每个通道$B_{00}^{(c=0)},B_{00}^{(c=1)},B_{00}^{(c=2)}$，总共的乘法操作次数为$3\times 9=27$,加法操作次数为$3\times 8=24$次。

2. 然后再将这些输入通道的数值相加，并且加上偏置参数 $b$
   $$B_{00}=B_{00}^{(c=0)}+B_{00}^{(c=1)}+B_{00}^{(c=2)}+b$$
   由于需要额外引入3次加法操作，所以最后总的加法操作次数是$24+3=27$
   由此可得计算出一个像素点需要乘法操作次数是27，加法操作次数也是27。

3. 输出特征图的大小是$[10,64,224,224]$，则总共需要乘法操作次数是：
   $$27\times 10\times 64\times 224\times 224=867041280$$
   加法操作次数和乘法操作次数相同都是867041280。