论文链接:https://arxiv.org/pdf/2405.14458
代码链接:https://github.com/THU-MIG/yolov10
解决了什么问题?
实时目标检测是计算机视觉领域的研究焦点,目的是以较低的延迟准确地预测图像中各物体的类别和坐标。它广泛应用于自动驾驶、机器人导航和目标跟踪等任务。近些年来,研究人员基本聚焦于 CNN 目标检测器,从而实现实时检测。由于 YOLO 能很好地平衡计算成本和检测表现,它已经成为了实时目标检测的主流方法。YOLO 的检测流程包括两个部分:模型前向计算和 NMS 后处理。这两个部分到现在仍然有一些缺陷,没达到准确率-效率的最优解。
YOLOs 在训练时通常使用“一对多”的标签分配策略,一个 ground-truth 目标会被分配给多个正样本。尽管表现不错,但它在推理时仍要通过 NMS 来选取最佳的正样本。这就降低了推理速度,模型表现对 NMS 的超参数很敏感,使 YOLO 无法实现端到端的部署。一个解决办法就是采用端到端 DETR 的架构。RT-DETR 提出了高效的混合编码器和最低不确定性的 qeury selection,促进了 DETR 的实时应用。但是,DETR 的复杂度很高,使它无法最优地平衡准确率和速度。另一个办法就是研究 CNN 端到端的目标检测器,通常使用“一对一”的标签分配策略,抑制重复的预测。但是,这会造成额外的推理开支或表现不佳。
此外,模型架构设计也很关键,它会影响准确率和推理速度。为了找到更高效的模型结构,研究人员探索了不同的设计策略。针对主干网络,人们提出了不同的基础计算单元来增强特征提取能力,比如 DarkNet、CSPNet、EfficientRep、ELAN 等。对于 neck 结构,人们提出了 PAN、BiC、GD 和 RepGFPN 来增强多尺度特征融合能力。此外,人们也研究了模型缩放策略和重参数化技术。尽管这些努力取得了显著的提升,但还是缺乏一个关于 YOLO 效率和准确率的全面研究。在 YOLOs 中仍然存在明显的计算冗余,使参数利用率不高,效率并非最佳的。
本文在后处理和模型架构方面,进一步发掘了 YOLO 的表现和效率的边界。为了在训练中省去 NMS,作者提出了双标签分配策略和一致的匹配度量,这样模型能在训练时获得丰富且均衡的监督信号,推理时无需 NMS,从而改善了表现、降低了推理延迟。此外,作者针对 YOLO 提出了全面的效率-准确率驱动的模型设计策略。本文从效率和准确率的角度出发,优化了 YOLO 的多个部分,极大地降低了计算成本、增强了模型能力。在效率方面,作者提出了一个轻量级的分类头、空间-通道解耦下采样、rank-guided 模块设计,从而降低计算冗余,使结构更加高效。在准确率方面,作者研究了大卷积核,提出了有效的局部自注意力模块,增强模型的能力。
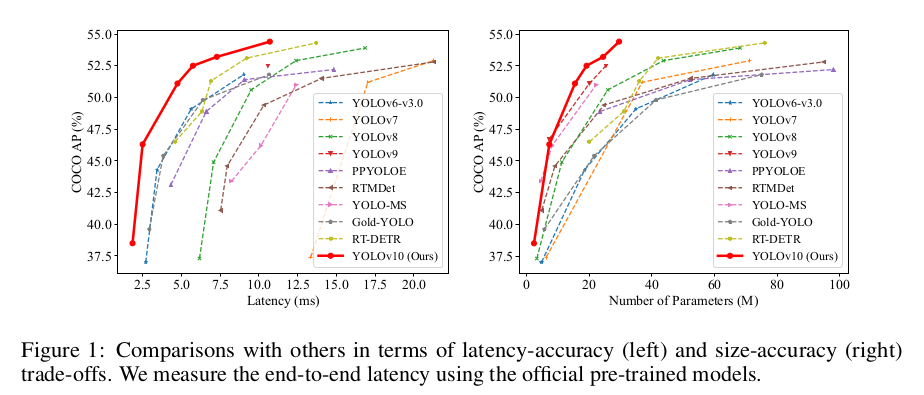
实验表明,各版模型大小的 YOLOv10 都取得了 SOTA 的表现和效率。例如,在 COCO 上,YOLOv10-S 要比 RT-DETR-R18 快 1.8 × 1.8\times 1.8× 倍,但 AP 相似,而且参数量和 FLOPs 要小 2.8 × 2.8\times 2.8× 倍。与 YOLOv9-C 相比,在表现接近的情况下,YOLOv10-B 的延迟要低 46 % 46\% 46%,参数量要少 25 % 25\% 25%。
提出了什么方法?
Consistent Dual Assignments for NMS-free Training
训练时,YOLOs 通常利用 TAL 为每个实例分配多个正样本。该“一对多”的分配策略会产生充足的监督信号,促进模型的优化和表现。但是,YOLOs 就必须依赖 NMS 后处理,部署时的推理效率就不是最优的。尽管之前的工作研究了“一对一”的匹配策略,抑制重复的预测,它们通常会增加推理成本,表现非最优。本文提出了一个无需 NMS 的策略,即双标签分配和一致的匹配度量,实现最优的效率和表现。
Dual Label Assignment
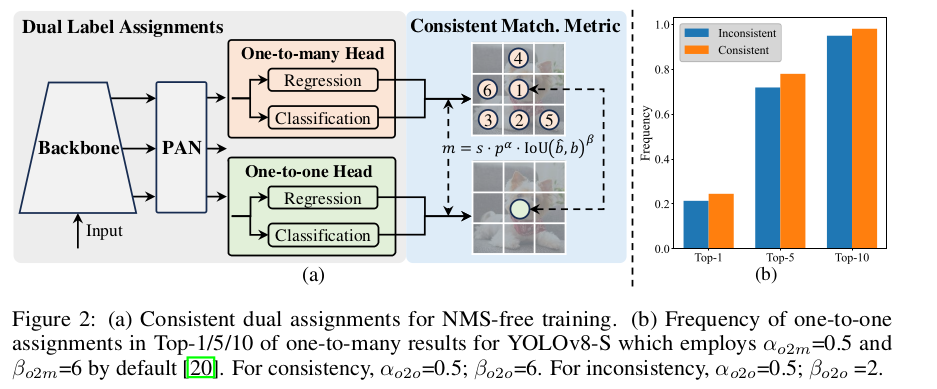
与“一对多”的分配策略不同,“一对一”的匹配策略为每个 ground-truth 分配一个预测框,避免了 NMS 后处理。但是,它会弱化监督信号,降低了准确率和收敛速度。幸运的是,我们可以通过“一对多”的分配策略来补偿该缺陷。作者为 YOLO 引入了双标签分配策略,结合了这俩策略的优点。如下图(a)所示,作者在 YOLOs 中融合了另一个“一对一”的 head。它保留了和原本“一对多”分支一样的结构,采用了相同的优化目标函数,但是利用了“一对一”的匹配策略来完成标签分配。训练时,两个 heads 协同优化,使主干网络和 neck 能获得“一对多”分配机制提供的丰富的监督信号。推理时,作者没有用“一对多”的 head,只使用了“一对一”的 head 做预测。这使得端到端部署 YOLO 时不会增加推理成本。此外,在“一对一”的匹配时,作者采用了 top-1 选项,取得的表现和匈牙利匹配一样,额外的训练时间要更少。
Consistent Matching Metric
分配时,“一对一”和“一对多”的方法都采用了一个度量,从而对预测框和 ground-truths 之间的一致性做量化评估。作者使用了一个一致的匹配度量:
m ( α , β ) = s ⋅ p α ⋅ IoU ( b ^ , b ) β m(\alpha, \beta)=s\cdot p^\alpha \cdot \text{IoU}(\hat{b},b)^\beta m(α,β)=s⋅pα⋅IoU(b^,b)β
其中 p p p是分类得分, b ^ \hat{b} b^和 b b b表示预测框和 ground-truth 框。 s s s表示空间先验,预测框的 anchor point 是否在 ground-truth 内。 α \alpha α和 β \beta β是两个重要超参数,平衡类别预测任务和定位回归任务的影响力。将“一对多”和“一对一”度量分别记做 m o 2 m = m ( α o 2 m , β o 2 m ) m_{o2m}=m(\alpha_{o2m}, \beta_{o2m}) mo2m=m(αo2m,βo2m) 和 m o 2 o = m ( α o 2 o , β o 2 o ) m_{o2o}=m(\alpha_{o2o}, \beta_{o2o}) mo2o=m(αo2o,βo2o)。这些度量会影响两个 heads 的标签分配和监督信息。
在双标签分配策略,“一对多”分支要比“一对一”分支提供更加丰富的监督信号。如果我们能使“一对一” head 的监督信号和“一对多” head 提供的信号一致,我们可以让“一对一” head 朝着“一对多” head 的优化方向来做优化。这样在推理时,“一对一” head 能提供更高质量的样本,表现就会更好。作者首先分析了这两个 heads 监督信号之间的差距。由于训练的随机性,作者用相同的值来初始化这俩 heads,产生相同的预测结果,也就是说,对于每对预测-ground-truth,“一对一” head 和“一对多” head 输出相同的 p p p 和 IoU \text{IoU} IoU。作者发现,这两个分支的回归目标互不冲突,因为匹配上的预测框会共享 ground-truth,而没有匹配上的框会被忽略掉。所以,监督差异就存在于分类目标。给定一个 ground-truth,我们将和预测框 IoU \text{IoU} IoU 最高的 ground-truth 记做 u ∗ u^\ast u∗,“一对多”和“一对一”最高的匹配分数记做 m o 2 m ∗ m_{o2m}^\ast mo2m∗和 m o 2 o ∗ m_{o2o}^\ast mo2o∗。假设“一对多”分支输出的正样本集合为 Ω \Omega Ω,“一对一”分支选取度量值为 m o 2 o = m o 2 o ∗ m_{o2o}=m_{o2o}^\ast mo2o=mo2o∗ 的第 i i i个预测框,然后我们可以推导 TAL 的分类目标为 t o 2 m , j = u ∗ ⋅ m o 2 m , j m o 2 m ∗ ≤ u ∗ , j ∈ Ω t_{o2m,j}=u^\ast \cdot \frac{m_{o2m,j}}{m_{o2m}^\ast}\leq u^\ast,\quad j\in \Omega to2m,j=u∗⋅mo2m∗mo2m,j≤u∗,j∈Ω, t o 2 o , i = u ∗ ⋅ m o 2 o , i m o 2 o ∗ ≤ u ∗ , j ∈ Ω t_{o2o,i}=u^\ast \cdot \frac{m_{o2o,i}}{m_{o2o}^\ast}\leq u^\ast,\quad j\in \Omega to2o,i=u∗⋅mo2o∗mo2o,i≤u∗,j∈Ω。这两个分支的监督差异因此就可以用不同分类目标函数的 1-Wasserstein 距离来推导,
A = t o 2 o , i − I ( i ∈ Ω ) t o 2 m , i + ∑ k ∈ Ω \ { i } t o 2 m , k A=t_{o2o,i}-\mathbb{I}(i\in \Omega)t_{o2m,i} + \sum_{k\in\Omega \backslash \{i\}} t_{o2m,k} A=to2o,i−I(i∈Ω)to2m,i+k∈Ω\{i}∑to2m,k
我们可以发现该差距会随着 t o 2 m , i t_{o2m,i} to2m,i增长而减少,即在 Ω \Omega Ω 中 i i i 的排序比较高。当 t o 2 m , i = u ∗ t_{o2m,i}=u^\ast to2m,i=u∗ 时,它达到最低,即它是 Ω \Omega Ω 中最优的正样本,如上图(a)所示。作者提出了一致的匹配度量,即 α o 2 o = r ⋅ α o 2 m \alpha_{o2o}=r\cdot \alpha_{o2m} αo2o=r⋅αo2m 和 β o 2 o = r ⋅ β o 2 m \beta_{o2o}=r\cdot \beta_{o2m} βo2o=r⋅βo2m,也就是说 m o 2 o = m o 2 m r m_{o2o}=m_{o2m}^r mo2o=mo2mr。因此,“一对多” head 的最佳正样本也是“一对一” head 的最佳正样本。于是,这俩 heads 都能一致地被优化。为了简洁,作者默认地取 r = 1 r=1 r=1,即 α o 2 o = α o 2 m \alpha_{o2o}=\alpha_{o2m} αo2o=αo2m, β o 2 o = β o 2 m \beta_{o2o}=\beta_{o2m} βo2o=βo2m。为了验证该监督对齐后的效果,作者在“一对多”匹配的结果里,数了“一对一”匹配上 top-1/5/10 的样本对。如上图2(b) 所示,有了一致的匹配度量后,对齐效果得到改善。
Holistic Efficiency-Accuracy Driven Model Design
除了后处理,YOLO 模型的结构也是一个挑战。尽管之前的工作研究了各种设计策略,但仍欠缺一个对 YOLO 各构成的系统全面的分析。模型架构带来不可忽视的计算冗余,制约了性能。于是,作者从效率和准确率的角度,系统地分析了模型架构的设计。
Efficiency driven model design
YOLO 由 stem、下采样层、基础构建模块构成的 stages 和 head 组成。Stem 带来的计算成本不多,因此作者从另外三个部分下手。
轻量级的分类 head
在 YOLO 中,分类和回归 heads 通常共享相同的结构。但是,它们的计算成本是明显不同的。例如,在 YOLOv8-S 中,分类 head 的计算量和参数量( 5.95 G / 1.51 M 5.95G/1.51M 5.95G/1.51M)是回归 head ( 2.34 G / 0.64 M 2.34G/0.64M 2.34G/0.64M)的 2.5 × 2.5\times 2.5× 和 2.4 × 2.4\times 2.4×。但是,分析了分类损失和回归损失的影响后,作者发现回归 head 在 YOLO 的表现上要承担更加重要的角色。因此,作者可以降低分类 head 的成本,而无需担心表现变差。所以,作者只为分类 head 使用了一个轻量级的结构,包括两个深度可分离卷积(核大小是 3 × 3 3\times 3 3×3),后面是一个 1 × 1 1\times 1 1×1卷积。
空间-通道解耦下采样
YOLOs 通常使用标准的 3 × 3 3\times 3 3×3 卷积,步长为 2 2 2,同时做空间下采样(从 H × W H\times W H×W变到 H 2 × W 2 \frac{H}{2}\times \frac{W}{2} 2H×2W)和通道变换(从 C C C 变成 2 C 2C 2C)。这回引入的计算量约为 O ( 9 2 H W C 2 ) \mathcal{O}(\frac{9}{2}HWC^2) O(29HWC2),参数量约为 O ( 18 C 2 ) \mathcal{O}(18C^2) O(18C2)。相反,作者提出将空间尺寸降低和通道增加的操作解耦,使下采样更加高效。首先利用 pointwise 卷积来调节通道维度,然后利用深度卷积来进行空间下采样。这就将计算成本降低到了 O ( 2 H W C 2 + 9 2 H W C ) \mathcal{O}(2HWC^2+\frac{9}{2}HWC) O(2HWC2+29HWC),参数量为 O ( 2 C 2 + 18 C ) \mathcal{O}(2C^2 + 18C) O(2C2+18C)。同时在下采样时最大可能地保留信息,提升表现,降低延迟。
Rank-guided block design
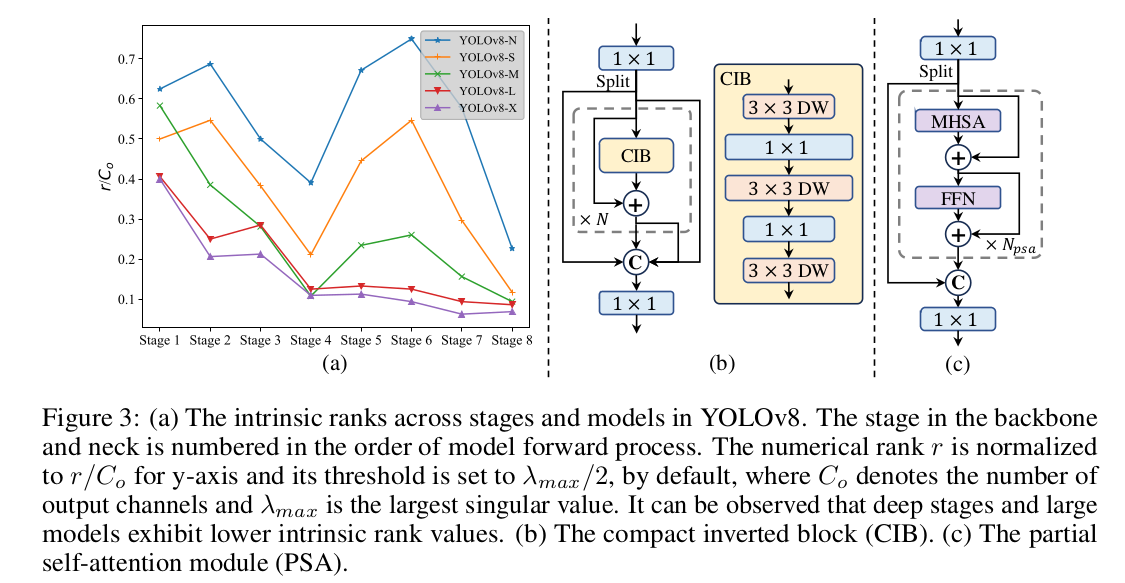
YOLOs 通常会在多个 stages 中用到相同的结构,比如 YOLOv8 的 bottleneck block。为了彻底地验证该设计,作者使用了 intrinsic rank 来分析每个 stage 的冗余性。作者计算每个 stage 最后一个基础模块的最后一个卷积的数值 rank,计数超过特定阈值的奇异值个数。下图(a) 展示了 YOLOv8,表明较深的 stages 和较大的模型存在更多的冗余。这个观察表明,给所有的 stages 简单地添加更多的相同模块并不是最优的。于是,作者提出了 rank-guided 模块设计,目的是降低冗余 stages 的复杂度。如下图b 所示,作者首先提出了一个紧凑的倒转模块(CIB)结构,采用廉价的深度卷积做空间混合,pointwise 卷积做通道混合。它可以作为基础构建模块用,嵌入到 ELAN 结构中。然后,作者提出了 rank-guided 模块分配策略来实现最优的效率,而保持模型性能。给定一个模型,我们根据 intrinsic rank 将所有的 stages 做升序排序。作者用 CIB 替换第一个 stage 的基础模块,进一步校验表现差异。如果表现没有退化,我们就在下一个 stage 继续该替换,不然就停止替换。因此,我们能跨 stages 和模型尺度,实现一个自适应的模块设计,实现更高的计算效率,而不会牺牲准确率。
Accuracy driven model design
作者进一步研究了大卷积核的卷积和自注意力,以最低的代价提升模型表现。
大卷积核卷积
大卷积核的深度卷积能有效地扩大感受野,增强模型表现。但是,直接在 stages 中使用它们会污染检测小目标的浅层特征,也会增加高分辨率 stages 的 I/O 开支和延迟。所以,作者提出在深度 stages 的 CIB 中使用大卷积核的深度卷积。作者增加 CIB 的第二个
3
×
3
3\times 3
3×3 深度卷积的卷积核大小为
7
×
7
7\times 7
7×7。此外,作者使用了结构重参数化技术,加入了另一个
3
×
3
3\times 3
3×3 深度卷积分支,降低优化难度,而不会增加推理代价。此外,由于模型大小增加,感受野自然地就变大了,使用大卷积核卷积的优势就没了。所以,作者只在小模型使用了大卷积核。
Partial self-attention
自注意力被广泛使用在各视觉任务上。但是,它带来的计算复杂度和内存占用都太高了。于是,作者提出了一个高效的局部自注意力模块设计,如上图© 所示。在
1
×
1
1\times 1
1×1 卷积后,作者将特征平均地拆分成两个部分。作者只将一个部分输入进由 multi-head 自注意力和 FFN 组成的
N
P
S
A
N_{PSA}
NPSA 模块。这俩部分然后 concat 一起,输入一个
1
×
1
1\times 1
1×1 卷积。此外,为了提高推理速度,在 MHSA 中,query 和 key 的维度是 value 的一半,将 LayerNorm 替换为了 BatchNorm。PSA 只放在了分辨率最低的 Stage 4 后,避免自注意力了高复杂度计算成本。这样,YOLO 中就加入了全局表征学习的能力,而且计算代价最低,很好地增强了模型能力,提升表现。