目录
- 前言
- 二分查找
- 例题一
- 例题二
- 例题三
- 例题四
前言
本篇文章记录了代码随想录二分查找算法的总结笔记,下面我们一起来学习吧!!
二分查找
关于二分查找算法,我在之前的这篇博客里面做了非常多的分析,但是后面做题做着发现二分又不会了,还是感觉自己对二分的边界条件不敏感或者说是没完成理解透彻,那么接下来我会通过对例题的逐步分析让大家不再对二分感到困惑!!
在代码随想录中关于二分查找提供了两种写法,这俩种写法其实就是我们解题的关键,下面我们就来逐个分析两种写法的不同与优势!!
第一种写法(左闭右闭):
// 版本一
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);
if (nums[middle] > target) {
right = middle - 1;
} else if (nums[middle] < target) {
left = middle + 1;
} else {
return middle;
}
}
// 未找到目标值
return -1;
}
};
Q:第一种写法的区间是左闭右闭,所以我们的循环条件为while (left <= right)?
当left == right是有意义的,为什么有意义呢?因为我们的设定的区间范围内的元素都是有可能为目标值的,假设我们要查找的target在最后一个位置,那么left一直向右缩小区间,最终left一定 == right,此时mid == left == right,找到了直接返回mid即可。
第二种写法(左闭右开):
// 版本二
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle;
} else if (nums[middle] < target) {
left = middle + 1;
} else {
return middle;
}
}
// 未找到目标值
return -1;
}
};
Q:该写法的区间为[left,right)左闭右开,循环条件为while(left < right)?
循环结束条件为left == right,因为此时的left == right是没有意义的,[left, right) == [left, left) == [left, left - 1]显然是没任何意义的。
Q:注意写法二与写法一right的区别,第一种写法为right = mid - 1,第二种写法为right = mid;为何??
其实本质上它们是一样的,因为写法二的right是右开区间它是取不到的,当right == mid,[left, right) == [left, mid) == [left, mid - 1]!!
上述对于俩种写法我们还并不知道它们的优缺点在哪?适用于何种场景?因为上述的二分查找场景是最简单的,下面我们通过例题来进行分析吧。
例题一
搜索插入位置

给出写法一的代码:
// 左闭右闭
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (nums[mid] < target) {
l = mid + 1;
} else if (nums[mid] > target) {
r = mid - 1;
} else {
return mid;
}
}
return r + 1; // 返回l也是可行的
}
};
相较于之前的普通二分查找这里就只是返回值改变了,之前的场景是找不到就返回-1,而现在是如果找不到还要返回正确的插入位置。那么对于写法一到底该返回left还是right呢?这里为何最终返回的是right + 1?left与right的位置关系如何呢?下面我们来验证一下:
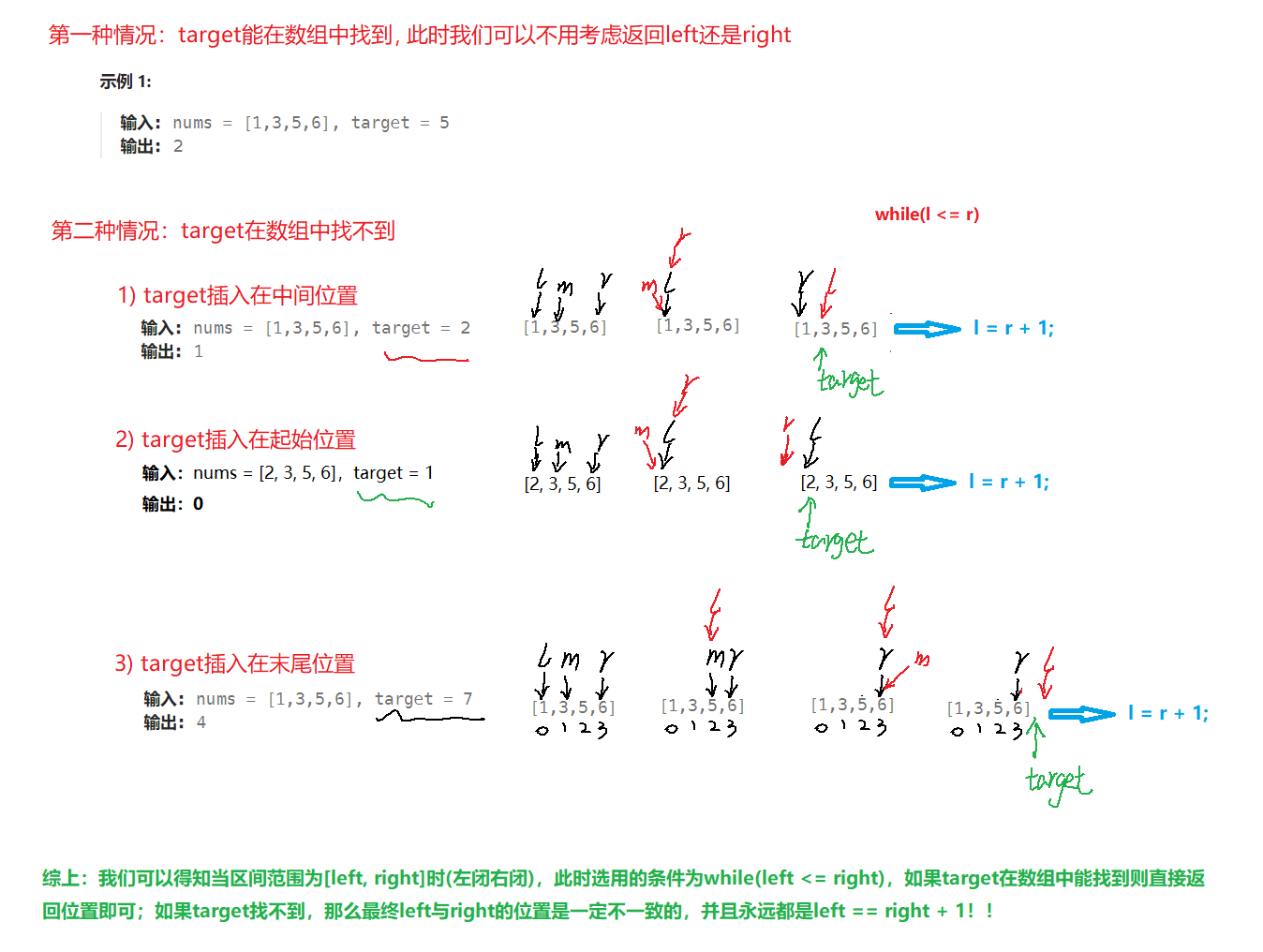
另外这里也可以将nums[mid] >= target合并为一步,找到第一个大于等于target元素的位置,注意条件一定不能是nums[mid] <= target, 这样找到的位置是最后一个小于等于target元素的位置,也即第一个大于target元素的位置!!
// 版本二
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return l;
}
};
为什么这种合并的写法也可以呢?其实合并的写法就包括了直接在数组中匹配到target对应的元素直接返回的情况,分析如下:

那么返回 l 或者 r + 1 的话都是符合直接匹配到相应的元素直接返回的,另外还包括了不匹配的情况。
写法二的代码(左闭右开):
// 版本一
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size();
while (l < r) {
int mid = l +(r - l) / 2;
if (nums[mid] < target) {
l = mid + 1;
} else if (nums[mid] > target) {
r = mid;
} else {
return mid;
}
}
return l; // r也可
}
};
// 版本二
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size();
while (l < r) {
int mid = l +(r - l) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
return l; // r也可
}
};
注意写法二返回left或right都可以,假设直接匹配到不直接返回的话也就是按照写法二的版本二,因为最终left一定 ==right 才能结束循环,所以返回left和right都可以。
从这里就可以看出写法二的优势:相较于写法一left != right需要考虑返回的位置,而写法二返回left与right都可以!后续当然我个人也比较推荐写法二哈哈,当然了其实理解透彻了这两种写法其实就是看哪种方便用哪种了,没必要去纠结这个问题。
例题二
我们接着来看下一道题:34. 在排序数组中查找元素的第一个和最后一个位置

思路:要解决这道题,首先我们得找到第一个大于等于该元素的位置,假设该位置的值不等于target那么就没必要找下去了,直接返回{-1,-1},因为第一个位置的元素都不相等那么后面肯定是没有的,并且如果该位置的索引为数组的个数的话(也就是要找的元素大于数组中所有的元素),此时也直接返回{-1, -1};如果该位置的元素等于target的话,那么很简单我们就继续向后查找最后一个相等元素的位置即可。
代码如下:
// 代码一:
class Solution {
public:
int lower_bound(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return l; // r + 1
}
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.size() == 0) return {-1, -1};
int start = lower_bound(nums, target);
if (start == nums.size() || nums[start] != target) return {-1, -1};
int end = lower_bound(nums, target + 1) - 1; // 找到第一个大于等于target+1的元素, 那么它减-1其实就为最后一个等于target的位置
return {start, end};
}
};
// 代码二:
class Solution {
public:
int lower_bound(vector<int>& nums, int target) {
int l = 0, r = nums.size();
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.size() == 0) return {-1, -1};
int start = lower_bound(nums, target);
if (start == nums.size() || nums[start] != target) return {-1, -1};
int end = lower_bound(nums, target + 1) - 1; // 找到第一个大于等于target+1的元素, 那么它减-1其实就为最后一个等于target的位置
return {start, end};
}
};
// 代码三:
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.size() == 0)
return {-1, -1};
int l = 0, r = nums.size();
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
if (r == nums.size() || nums[r] != target) return {-1, -1};
int pos = r + 1;
while (pos < nums.size() && nums[pos] == target) {
pos++;
}
return {r, pos - 1};
}
};
// 代码四:
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int l = -1, r = nums.size();
while (l + 1 != r) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid;
}
}
if (r == nums.size() || nums[r] != target) return {-1, -1};
int pos = r + 1;
while (pos < nums.size() && nums[pos] == target) {
pos++;
}
return {r, pos - 1};
}
};
// 代码五: STL大法
// lower_bound找到第一个大于等于target的元素, 并返回它的位置
// upper_bound找到第一个大于target的元素, 第一个大于target的位置-1,
// 即为最后一个小于等于target的位置, 因为前面找到了第一个大于等于target的位置, 所以这里一定能找到最后一个等于target的位置
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.size() == 0) return {-1, -1};
int l = lower_bound(nums.begin(), nums.end(), target) - nums.begin();
if (l == nums.size() || nums[l] != target) return {-1, -1};
int r = upper_bound(nums.begin(), nums.end(), target) - nums.begin();
return {l, r - 1};
}
};
例题三
下面我们来看这道题:69. x 的平方根

思路:这道题其实可以从搜索插入位置那道题得到很大的启发,结果返回x的平方根是向下取整的。这里同样的有两种情况,第一情况就是mid * mid刚好与x匹配此时直接返回即可,第二种情况就是找不到刚好匹配的就只能取最后一个小于x的那个位置,即第一个大于等于x的位置-1,所以根据上述一系列结论,我们从搜索插入位置那道题得到启发直接就返回right的位置即可(使用左闭右闭方法)!!
// 方法一: 左闭右闭
class Solution {
public:
int mySqrt(int x) {
// 特判, 防止出现除0错误
if (x <= 1) return x;
// 这里的右区间还能进行优化, 因为x的平方根它必定是小于等于x/2的。
//所以我们可以将右区间缩小至x / 2, 但是x == 2会出现除零错误, 此时我们要向上取整处理一下, 在外面或者在取mid时都可以
int l = 0, r = x; // r = x / 2 + 1也可
while (l <= r) {
int mid = l + (r - l) / 2;
if (mid > x / mid) {
r = mid - 1;
} else if (mid < x / mid) {
l = mid + 1;
} else {
return mid;
}
}
return r; // l - 1都可
}
};
// 优化版:
class Solution {
public:
int mySqrt(int x) {
// 特判, 防止出现除0错误
if (x <= 1) return x;
int l = 0, r = x / 2;
while (l <= r) {
int mid = l + (r - l + 1) / 2;
if (mid > x / mid) {
r = mid - 1;
} else if (mid < x / mid) {
l = mid + 1;
} else {
return mid;
}
}
return r;
}
};
// 第二种写法: 左闭右开
class Solution {
public:
int mySqrt(int x) {
// 特判, 防止出现除0错误
if (x <= 1) return x;
int l = 0, r = x + 1; // 开区间
while (l < r) {
int mid = l + (r - l) / 2;
if (mid > x / mid) {
r = mid;
} else if (mid < x / mid) {
l = mid + 1;
} else {
return mid;
}
}
return l - 1; // 实际上l与r都是第一个大于等于target的元素, 因此最后一个小于x元素的位置就为 l - 1 or r - 1!!
}
};
第一种写法较第二种写法的优点:第一种写法的left与right分别代表第一个大于等于target元素的位置、最后一个小于target元素的位置,它能明确代表俩个位置,但缺点就是返回时要考虑清楚返回left还是right;第二种写法的优点就是可以随意返回left与right的位置,但是它们都只能代表第一个大于等于target元素这一个位置,但是我们清楚了它们之间的关系之后,其实第二种写法是更不容易失误的嘿嘿!!
例题四
最后我们来看一道题:367. 有效的完全平方数
这道题乍一看不就是完全平方数嘛,只是返回true还是false的问题,当x的平方根刚好匹配时返回true,不匹配直接就返回false,可以说比上道题简单了不少,也确实是这样,但是我们不能照搬上面的代码:
// 下面这样是错误的
class Solution {
public:
bool isPerfectSquare(int num) {
int l = 0, r = num / 2;
while (l <= r) {
int mid = l + (r - l) / 2;
if (mid > num / mid) {
r = mid - 1;
} else if (mid < num / mid) {
l = mid + 1;
} else {
return true;
}
}
return false;
}
};
为何上述代码是错的呢?首先我们的思路肯定没问题,那么就一定是代码方面出现了问题,我们注意到在上一道题中我们的mid是跟num/mid进行比较的,这样是为了防止整数溢出,那么对于这道题能这么干吗?假设x == 5,此时mid = 2,mid == num / mid,返回true,但实际上5的平方根不为2啊返回false才对,为什么这里出现了错误?原因是num / mid是向下取整的,所以我们不能这么干,那就只有老老实实的判断mid * mid与num的大小了,并且我们不能用int来保存了,应该用long或者long long来保存才不会使得整数溢出,代码如下:
class Solution {
public:
bool isPerfectSquare(int num) {
long long l = 1, r = num;
while (l <= r) {
long long mid = l + (r - l) / 2;
if (mid * mid > num) { // 不能用除法 会向下取整的
r = mid - 1;
} else if (mid * mid < num) {
l = mid + 1;
} else {
return true;
}
}
return false;
}
};
// 左闭右开
class Solution {
public:
bool isPerfectSquare(int num) {
long long l = 1;
long long r = (long long)num + 1;
while (l < r) {
long long mid = l + (r - l) / 2;
if (mid * mid > num) { // 不能用除法 会向下取整的
r = mid;
} else if (mid * mid < num) {
l = mid + 1;
} else {
return true;
}
}
return false;
}
};
// 代码三:
class Solution {
public:
int mySqrt(int x) {
if(x == 1 || x == 0)
return x;
long l = -1, r = x;
while(l + 1 != r)
{
long mid = (l + r) / 2;
if(mid * mid <= x)
l = mid;
else
r = mid;
}
return l;
}
};
注意上述代码三是最为巧妙的一种方式,可以解决取整问题以及边界问题,大家还是可以看我之前的这篇博客去了解。