捕食者优化算法(Hunter–prey optimization,HPO)是一种受自然启发的群智能优化算法。该算法的灵感来自于捕食动物(如狮子、豹和狼)以及猎物(如雄鹿和瞪羚)的行为。动物狩猎行为有很多场景,其中一些场景已经转化为优化算法。本文使用的场景不同于以往算法的场景。在提出的方法中,猎物和捕食者种群,捕食者攻击远离猎物种群的猎物。猎人调整他的位置朝向远处的猎物,猎物也调整他的位置朝向安全的地方。搜索代理的位置是适应度函数的最佳值,被认为是安全的地方。

该成果于2022年发表在计算机领域三区期刊Algorithm and applications上,目前在谷歌学术上被引率134次。

狩猎-猎物循环是种群生物学中最引人注目的观察之一,本文所考虑的场景不同于其他场景。本文的场景是猎人寻找猎物,因为猎物通常是成群的,猎人选择一个远离群体的猎物。当猎人找到猎物后,他会追逐猎物。与此同时,猎物在捕食者的攻击中寻找食物和逃脱,并到达一个安全的地方。
1、算法原理
(1)种群初始化
首先,将初始种群随机设置为 ,然后将目标函数计算为 。种群的控制和指导在搜索空间中使用一系列的规则和策略所提出的算法的启发。重复该过程,直到算法停止。在每一次迭代中,种群中的每个成员的位置根据所提出的算法的规则进行更新,并与目标函数的新的位置进行评估。这个过程使得解决方案在每次迭代中得到改进。初始种群的每个成员的位置是在搜索空间中随机生成的,公式如下
其中Xi是猎人位置或猎物,lb是问题变量的最小值(下边界),ub是问题变量的最大值(上边界),d是问题的变量数(维数)。以下公式定义了搜索空间的下边界和上边界。
(2)目标函数定义
在生成初始种群并确定每个智能体的位置之后,使用目标函数 来计算每个解决方案的适应度。F(x)可以是最大值(效率、性能等)或最小值(成本、时间等)。计算适应度函数决定了哪个解决方案是好的还是坏的。在发现有希望的区域之后,必须减少随机行为,以便算法能够在有希望的区域周围搜索,这涉及到开发。对于猎人搜索机制,本文提出以下公式
方程更新了猎人的位置,其中x(t)是当前猎人的位置,x(t +1)为猎人的下一个位置,Ppos为猎物的位置,Z为由下式计算的自适应参数。

式中,R1、R3为[0,1]范围内的随机向量,P为0、1等于问题变量个数的随机向量,R2为[0,1]范围内的随机数, IDX为满足条件(P = 0)的向量R1的索引号。
C是勘探和开发之间的平衡参数,其值在迭代过程中从1减小到0.02。C的计算公式如下:
其中,它是当前迭代值,MaxIt是迭代的最大次数。如图所示,计算猎物的位置(Ppos),因此首先根据以下公式计算所有位置(l)的平均值,然后计算每个搜索代理与该平均位置的距离
根据以下公式计算基于欧几里得距离的距离。
根据以下公式,将距离位置均值距离最大的搜索代理称为猎物(Ppos)。
如果每次迭代中总是考虑与平均位置距离最大的搜索代理,则算法收敛较晚。根据狩猎场景,当猎人捕获猎物时,猎物会死亡,下一次,猎人会转向新的猎物。为了解决这个问题,本文考虑一个递减机制,公式如下
其中N为搜索代理的数量。
现在,本文将猎物位置计算为以下公式
下图显示了在算法运行期间如何计算Kbest和选择猎物(Ppos)。在算法开始时,Kbest的值等于N(搜索代理数)。因此,最后一个距离搜索agent平均位置(l)最远的搜索agent被选择为猎物,并被猎人攻击。如图所示,Kbest值逐渐减小,以至于在算法结束时,Kbest值等于第一个搜索代理。需要说明的是,在每次迭代中,搜索代理是根据到搜索代理平均位置的距离来排序的。

当猎物受到攻击时,它会试图逃离并到达安全的地方。
本文假设最安全的位置是全局最优的位置,因为它会给猎物更大的生存机会,猎人可能会选择其他猎物。提出下式来更新猎物位置
其中x(t)是猎物的当前位置,x (t+1)为猎物的下一个位置,Tpos为全局最优位置,Z为自适应参数,R4为[- 1,1]范围内的随机数。C是探索和开发之间的平衡参数,其值随着算法的迭代而减小。COS函数及其输入参数允许下一个猎物位置定位在全局最优的不同径向和角度,从而提高捕食阶段的性能。
这里出现的问题是如何在这个算法中选择猎人和猎物。为了回答这个问题,本文将等式结合起来。
其中R5是范围[0,1]内的随机数,b是调节参数,其在本研究中的值设定为0.1。如果R5值小于B,则搜索代理被认为是猎人,并且搜索代理的下一个位置用等式更新。
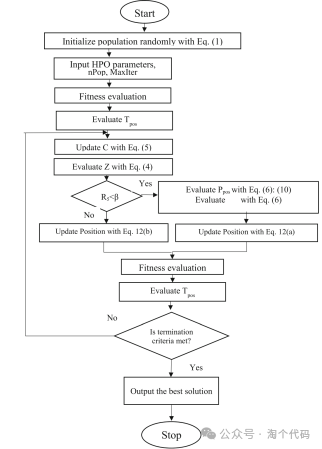
HPO对应的算法流程图如下所示。
2、结果展示
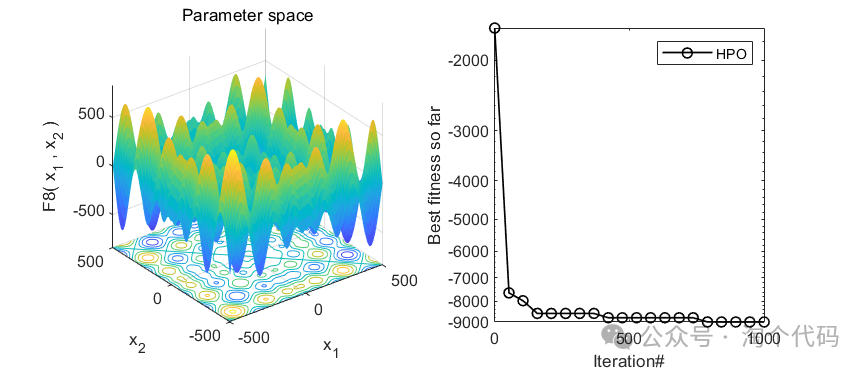
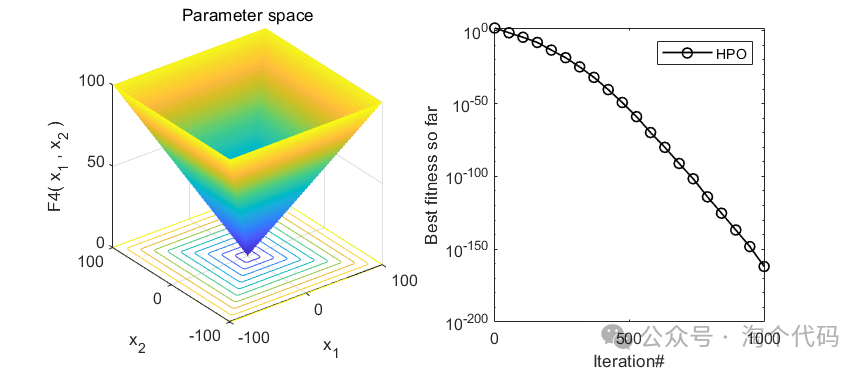
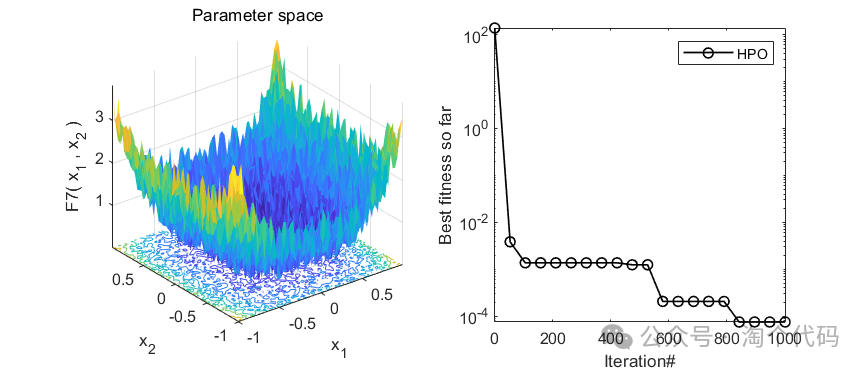
3、MATLAB核心代码
%% 淘个代码 %%
% 微信公众号搜索:淘个代码,获取更多代码
% 捕食者优化算法(HPO)
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
clear;
close all;
tic
function_name='F1';
[dim,CostFunction,ub, lb] = Select_Functions(function_name);
%% HPO Parameters
MaxIt = 500; % Maximum Nomber of Iterations
nPop = 30; % Population Size
Convergence_curve = zeros(1,MaxIt);
% Constriction Coefeicient
B = 0.1;
%% Initialization
HPpos=rand(nPop,dim).*(ub-lb)+lb;
% for i=1:nPop
% HPposFitness(i)=inf;
% end
% Evaluate
for i=1:size(HPpos,1)
HPposFitness(i)=CostFunction(HPpos(i,:));
end
% NFE = nPop;
[~,indx] = min(HPposFitness);
%
Target = HPpos(indx,:); % Target HPO
TargetScore =HPposFitness(indx);
Convergence_curve(1)=TargetScore;
%nfe = zeros(1,MaxIt);
%% HPO Main Loop
for it = 2:MaxIt
c = 1 - it*((0.98)/MaxIt); % Update C Parameter
kbest=round(nPop*c); % Update kbest
for i = 1:nPop
r1=rand(1,dim)<c;
r2=rand;
r3=rand(1,dim);
idx=(r1==0);
z=r2.*idx+r3.*~idx;
% r11=rand(1,dim)<c;
% r22=rand;
% r33=rand(1,dim);
% idx=(r11==0);
% z2=r22.*idx+r33.*~idx;
if rand<B
xi=mean(HPpos);
dist = pdist2(xi,HPpos);
[~,idxsortdist]=sort(dist);
SI=HPpos(idxsortdist(kbest),:);
HPpos(i,:) =HPpos(i,:)+0.5*((2*(c)*z.*SI-HPpos(i,:))+(2*(1-c)*z.*xi-HPpos(i,:)));
else
for j=1:dim
rr=-1+2*z(j);
HPpos(i,j)= 2*z(j)*cos(2*pi*rr)*(Target(j)-HPpos(i,j))+Target(j);
end
end
HPpos(i,:) = min(max(HPpos(i,:),lb),ub);
% Evaluation
HPposFitness(i) = CostFunction(HPpos(i,:));
% Update Target
if HPposFitness(i)<TargetScore
Target = HPpos(i,:);
TargetScore = HPposFitness(i);
end
end
Convergence_curve(it)=TargetScore;
disp(['Iteration: ',num2str(it),' Best Cost = ',num2str(TargetScore)]);
end
toc参考文献
[1]Naruei I, Keynia F, Sabbagh Molahosseini A. Hunter–prey optimization: Algorithm and applications[J]. Soft Computing, 2022, 26(3): 1279-1314.
完整代码获取
后台回复关键词:
TGDM166