两篇文章讲透数据结构之堆（一）！

1.堆的概念

2.堆的实现方式

3.堆的功能

4.堆的声明

5.堆的实现

5.1堆的初始化

5.2堆的插入

5.2.1向上调整算法

5.2.2堆的插入

5.3堆的删除

5.3.1向下调整算法

5.3.2堆的删除

5.4获取堆顶元素

5.5获取堆的元素个数

5.6判断堆是否为空

5.7打印堆

5.8建堆

5.8.1向上调整建堆

5.8.2向下调整建堆

5.9销毁堆

1.堆的概念

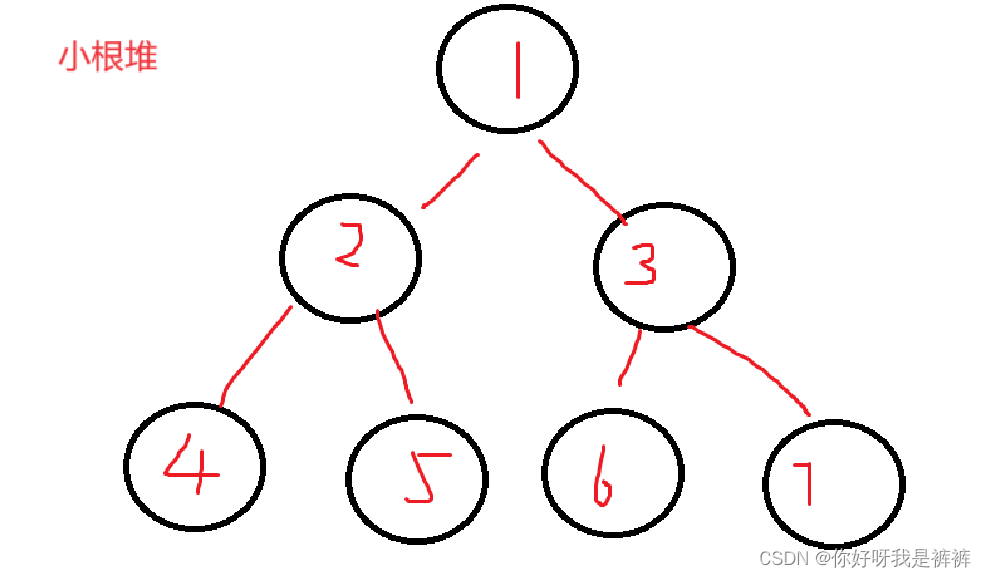
堆（Heap）可以被看作一种特殊的数据结构，堆通常是一个可以被看成完全二叉树的数组对象。

根据堆的数值的关系，可以将堆分为两类:

若满足任意结点的值>=其子结点的值，则可称为大根堆。
若满足任意结点的值<=其子结点的值，则可称为小根堆。

通俗解释来说：

若是任意一个根结点的值都大于其子结点，则被称为大根堆，因为根大！

若是任意一个根结点的值都小于子结点，则是小根堆，因为根小！

2.堆的实现方式

既然堆是一种二叉树，那么我们就可以采用链式存储或者数组存储来实现这个数据结构。但是考虑到完全二叉树的特性，我们在这里采用数组存储的方式，因为这样既方便访问，也不会浪费空间。

既然使用数组存储，就会用到下标，而我们每次插入和删除，都需要计算父结点和子结点的位置。

现在我们取出大根堆的前五个元素，并总结一下父节点和子结点下标的关系。

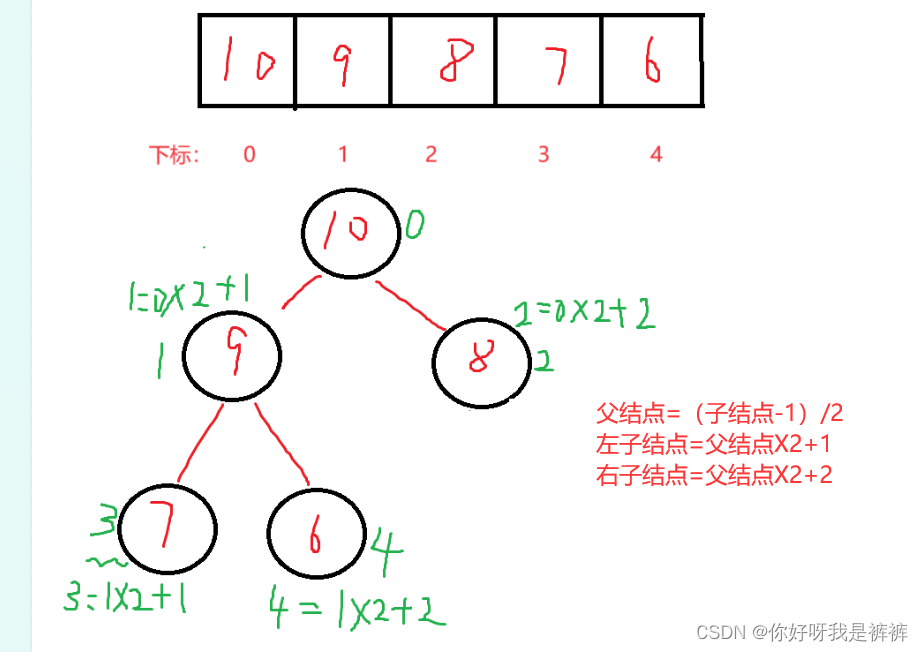
我们可以总结出上图红字的规律，现在我们具体推导一下这个规律。

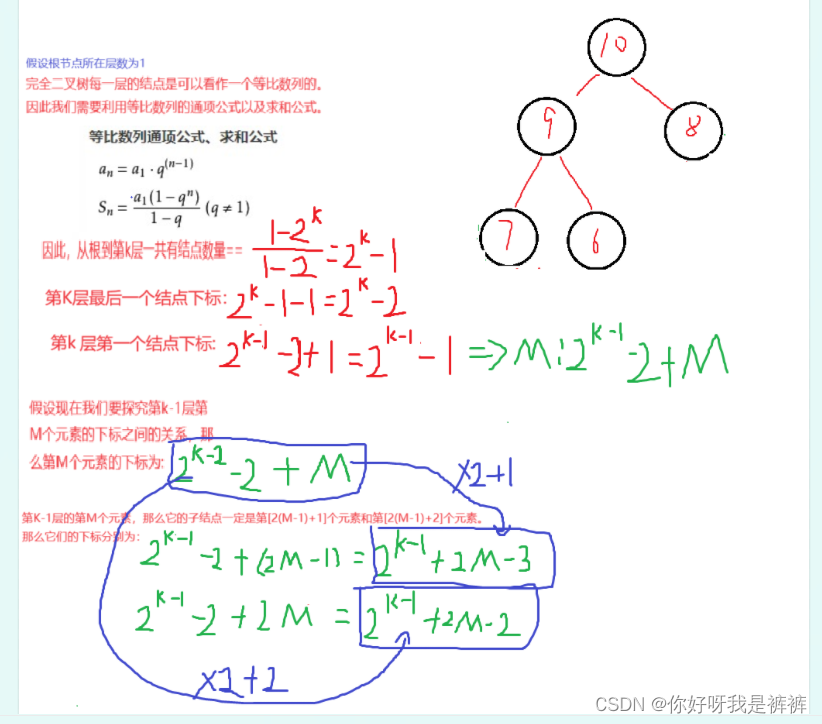
因此，我们可以得到如下结论：

若双亲节点存在，则其下标为(i-1)/2。
若孩子节点存在，左孩子下标为2i+1，右孩子为2i+2。

3.堆的功能

堆的初始化。
堆的插入。
堆的删除。
获取堆顶的元素。
堆的元素个数。
堆的判空。
输出堆。
建堆。
销毁堆

4.堆的声明

因为我们是用数组创建堆的，因此堆的声明和顺序表的声明类似！

typedef int HpDataType;
typedef struct Heap
{
	HpDataType* a;//存储数据
	int size;//大小
	int capacity;//容量
}Heap

5.堆的实现

5.1堆的初始化

堆的初始化与顺序表的初始化类似。

void HeapInit(Heap* hp)//堆的初始化
{
	assert(hp);
	hp->a = NULL;//初始化的时候也可以不开空间
	hp->capacity = 0;
	hp->size = 0;
    //hp->size=hp->capacity=0;
}

5.2堆的插入

我们插入一个值进入堆，是进入到堆目前最后一个元素的后面吗？

其实并不一定，我现在给出大家这么一个场景。

如果目前有如此一个大堆：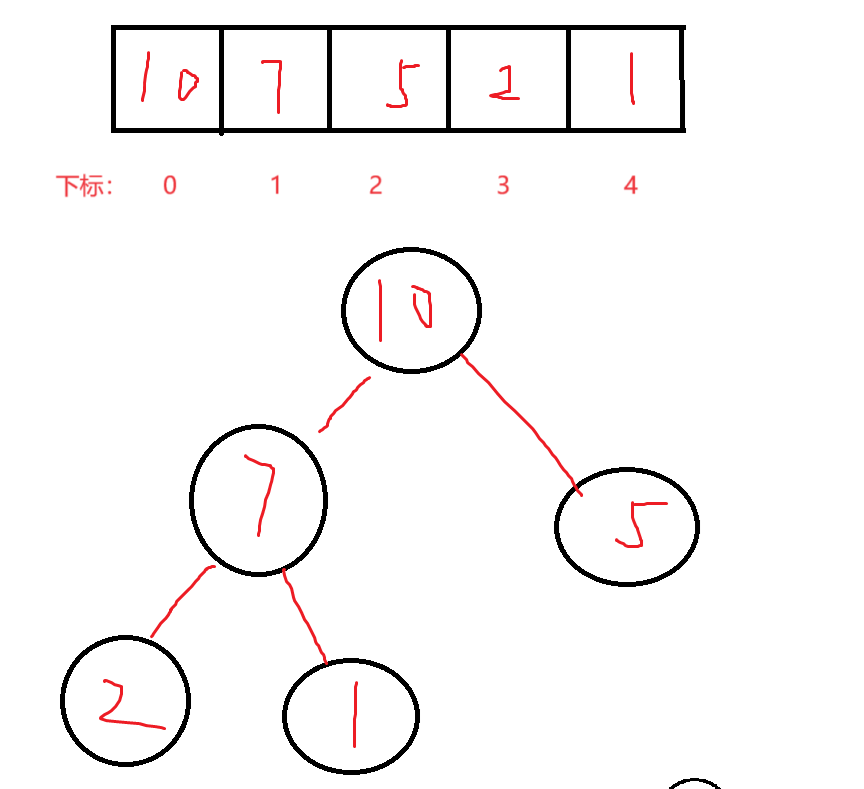

现在我们要往里插入一个8，是插入到下标为5的地方吗？

肯定不是的，那么他应该插入到什么地方呢？

很显然，他应该取代掉5的位置，那么，新的堆就应该是下图：

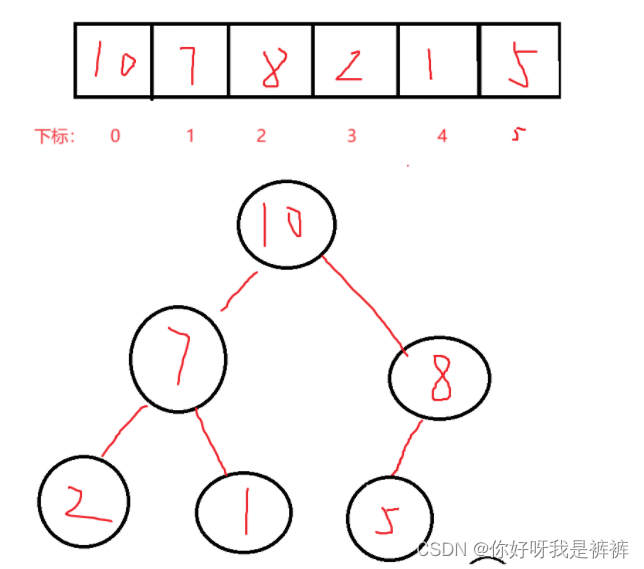
那么我们应该如何达到这个效果呢？

我们刚刚已经计算了父节点和子节点的关系，而由于堆是一个完全二叉树，我们在这里先插入其左结点再插入右结点。而左节点和右节点之间是没有大小关系的，因此我们插入结点之后需要和其父节点比较大小关系，如果比父结点大的话就交换，小的话就不动即可。

而如果第一次比较会发生交换，由于我们不确定它与更上一层的父结点的大小关系，因此我们还需要继续进行比较，直到不会发生交换为止。

于是乎，向上调整算法诞生了！

5.2.1向上调整算法

void AdjustUp(Heap* hp, int child)//向上调整
{
	int parent = (child - 1) / 2;
	while (child > 0)//循环结束条件是孩子成为了根节点
	{
		if (hp->a[child] > hp->a[parent])
		{
			//交换
			swap(&hp->a[child], &hp->a[parent]);//这个函数自己写
			//更新新的父结点和子结点
			child = parent;
			parent = (child - 1) / 2;
		}
		//没有发生交换就跳出
		else
		{
			break;
		}
	}
}

5.2.2堆的插入

现在我们就可以着手于完成堆的插入了。

void HeapPush(Heap* hp, HpDataType x)//堆的插入
{
	assert(hp);
	//判断是否开空间
	if (hp->size == hp->capacity)
	{
		int newcapacity = hp->capacity == 0 ? 4 : hp->capacity*2;
		HpDataType* tmp = (HpDataType*)realloc(hp->a, newcapacity * sizeof(HpDataType));
		if (!tmp)
		{
			perror("realloc fail");
			exit(1);
		}
		hp->a = tmp;
		hp->capacity = newcapacity;
	}
	//更新数值  后置++，先使用，再++
	hp->a[hp->size++] = x;
	AdjustUp(hp, hp->size - 1);
}

5.3堆的删除

堆的删除是删除堆顶元素，但是问题又出现了，删除了堆顶元素之后，后面的元素怎么办？顺着继承上去吗？那堆原来的亲属关系就全乱了，属实是父子叔侄变兄弟，闹了个哄堂大孝了。

那么这里我们要怎么处理呢？

我们在这里选择的处理方式是，先将堆顶元素和堆尾元素互换位置，之后直接让数组的长度-1。之后再调整根结点和其子节点之间的关系。调整的方法称为向下调整算法

5.3.1向下调整算法

刚刚已经介绍过了向上调整算法，我们也可以推测出向下调整算法的原理是和父节点和子节点的不断比较，但是这里又出现了一个问题，我们要和左子节点还是右子节点比较？

结论:

大堆，则根结点和子结点中较大的值比较
小堆，则根结点和子结点中较小的值比较

原理：这里以大堆为例，如果我们让根结点和较小的孩子值比较，而且发生了交换的话，那么现在的根结点是小于原来较大的孩子的，有悖于堆的定义。

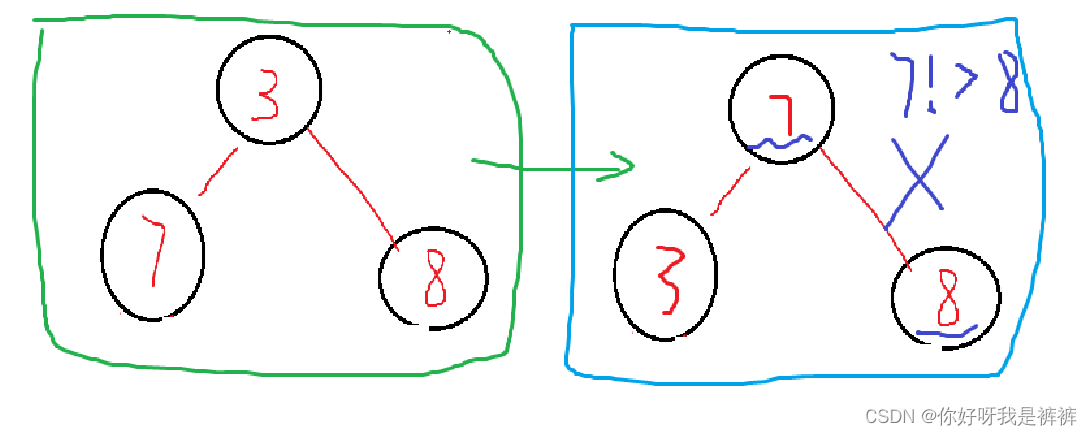
现在我们实现一下向下调整算法

void AdjustDown(int* a, int n, int parent);
{
	int child = parent * 2 + 1;//假设左孩子更大
	while (child < n)//当交换到最后一层后，无法再进行交换
	{//  右孩子的存在条件   右孩子比左孩子大,让右孩子比
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;//右孩子
		}
		if (&a[child] > a[parent])
		{
			//交换数值
			swap(&a[child], &a[parent]);
			//交换下标
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

5.3.2堆的删除

堆的删除的思路刚刚已经说过了，我们现在完成它即可。

void HeapPop(Heap* hp)//删除堆顶元素
{
	assert(hp);
	assert(hp->size > 0);
	swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}

5.4获取堆顶元素

获取堆顶元素，首先要确保堆存在而且堆内有元素。

我们返回堆顶元素，直接返回数组中的第一个元素即可。

HpDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	return hp->a[0];
}

5.5获取堆的元素个数

获取堆的元素个数，就是返回堆的size，我们直接返回即可。

int HeapSize(Heap* hp)//堆的大小
{
	assert(hp);
	return hp->size;
}

5.6判断堆是否为空

判断堆是否为空，就是判断hp的size成员是否等于0，也是直接返回即可。

bool HeapEmpty(Heap* hp)//判空
{
	assert(hp);
	return hp->size == 0;
}

5.7打印堆

数组的打印谁不会啊？

void HeapDisplay(Heap* hp)//堆的打印
{
	for (int i = 0; i < hp->size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}

5.8建堆

建堆，就是给一个数组不断的调整，调整成为一个堆。

因此我们要传入的参数为堆、数组、数组长度。

首先，我们要在堆中开辟一块和数组空间等大的空间来存储数组元素。

之后，我们需要将参数中的数组中的元素拷贝到我们创建的空间中。

再之后，我们就可以通过我们的调整算法建堆了。

5.8.1向上调整建堆

向上调整建堆就是采用向上调整算法建堆，在这里我们可以用堆的插入取代上述开辟内存的操作。

void HeapCreatUp(Heap* hp, HpDataType* arr, int n)
{
	assert(hp && arr);
	//将每个元素向上调整即可
	for (int i = 0; i < n; i++)
	{
		HeapPush(hp, arr[i]);
	}
}

5.8.2向下调整建堆

向下调整建堆就是采取向下算法建堆，在这里我们首先要给堆开辟一个内存，然后拷贝内存，最后采用向下调整算法建堆即可。

void HeapCreatDown(Heap* hp, HpDataType* arr, int n)
{
	assert(hp && arr);
	//给堆开辟内存
	HpDataType* tmp = (HpDataType*)malloc(sizeof(HpDataType) * n);
	if (tmp == NULL)
	{
		perror("malloc fail!");
		exit(-1);
	}
	hp->a = tmp;
	//将arr中的元素拷贝到堆中
	memcpy(hp->a, arr, sizeof(HpDataType) * n);
	hp->size = n;
	hp->capacity = n;
	//         最后一个父节点下标          父节点-1
	for (int i =((n - 1) - 1) / 2; i >= 0; i--)
	{                   
		AdjustDown(hp->a, n, i);
	}
}

5.9销毁堆

与顺序表的销毁方式一样，直接销毁即可。

void HeapDestroy(Heap* hp)//销毁堆
{
	assert(hp);
	free(hp->a);
	hp->size = hp->capacity = 0;
}

6.堆的头文件

Heap.h

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<assert.h>
#include <stdbool.h>
typedef int HpDataType;
typedef struct Heap
{
	HpDataType* a;//存储数据
	int size;//大小
	int capacity;//容量
}Heap;
void HeapInit(Heap* hp);//堆的初始化
void AdjustUp(Heap* hp, int child);//向上调整
void HeapPush(Heap* hp, HpDataType x);//堆的插入
bool HeapEmpty(Heap* hp);//判断堆是否为空
size_t HeapSize(Heap* hp);//堆的大小
void AdjustDown(int* a, int n, int parent);//向下调整
void HeapPop(Heap* hp);//删除堆顶元素
HpDataType HeapTop(Heap* hp);//获取堆顶元素
void HeapDisplay(Heap* hp);//堆的打印
void HeapDestroy(Heap* hp);//销毁堆
void HeapCreatUp(Heap* hp, HpDataType* arr, int n);//向上调整建堆
void HeapCreatDown(Heap* hp, HpDataType* arr, int n);//向下调整建堆