目录
python_jail
简单的rsa
托马斯.杰斐逊
这不是md5
进制转换
affine
Crack it
rsa
python_jail
启动场景
使用虚拟机nc进行连接
输入print(flag)
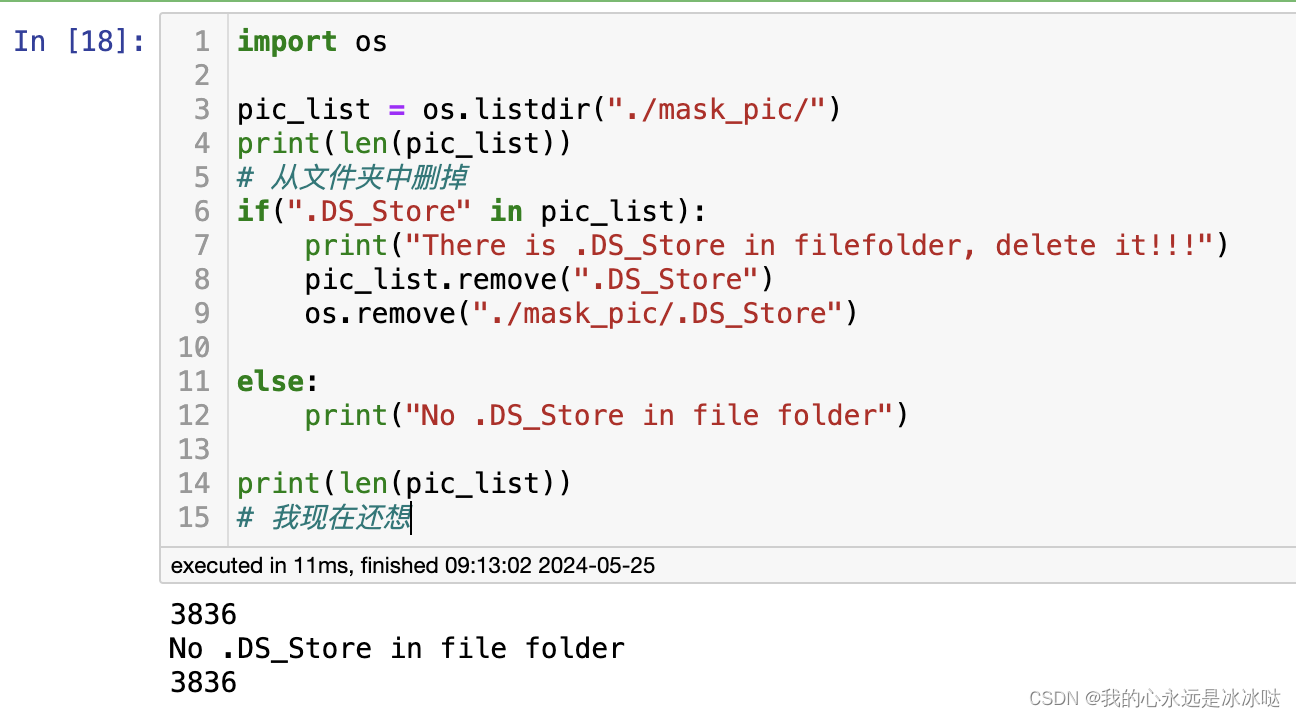
发现报错,经过测试只能传入10个字符多了就会报错
利用python中help()函数,借报错信息带出flag变量值内容, 刚好10个字符
输入:help(flag)
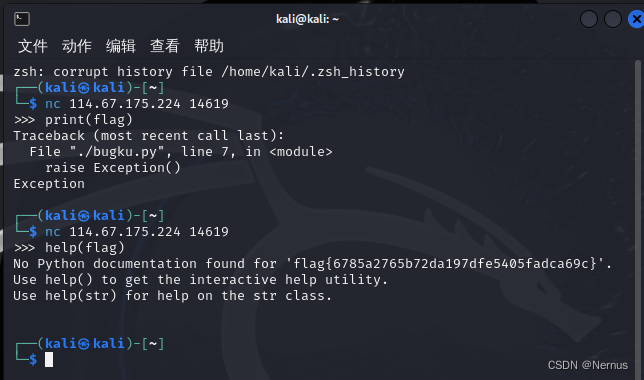
得到flag
flag{6785a2765b72da197dfe5405fadca69c}
简单的rsa
下载文件得到rsa.pyc
直接丢到在线python反编译网址
python反编译 - 在线工具 (tool.lu)
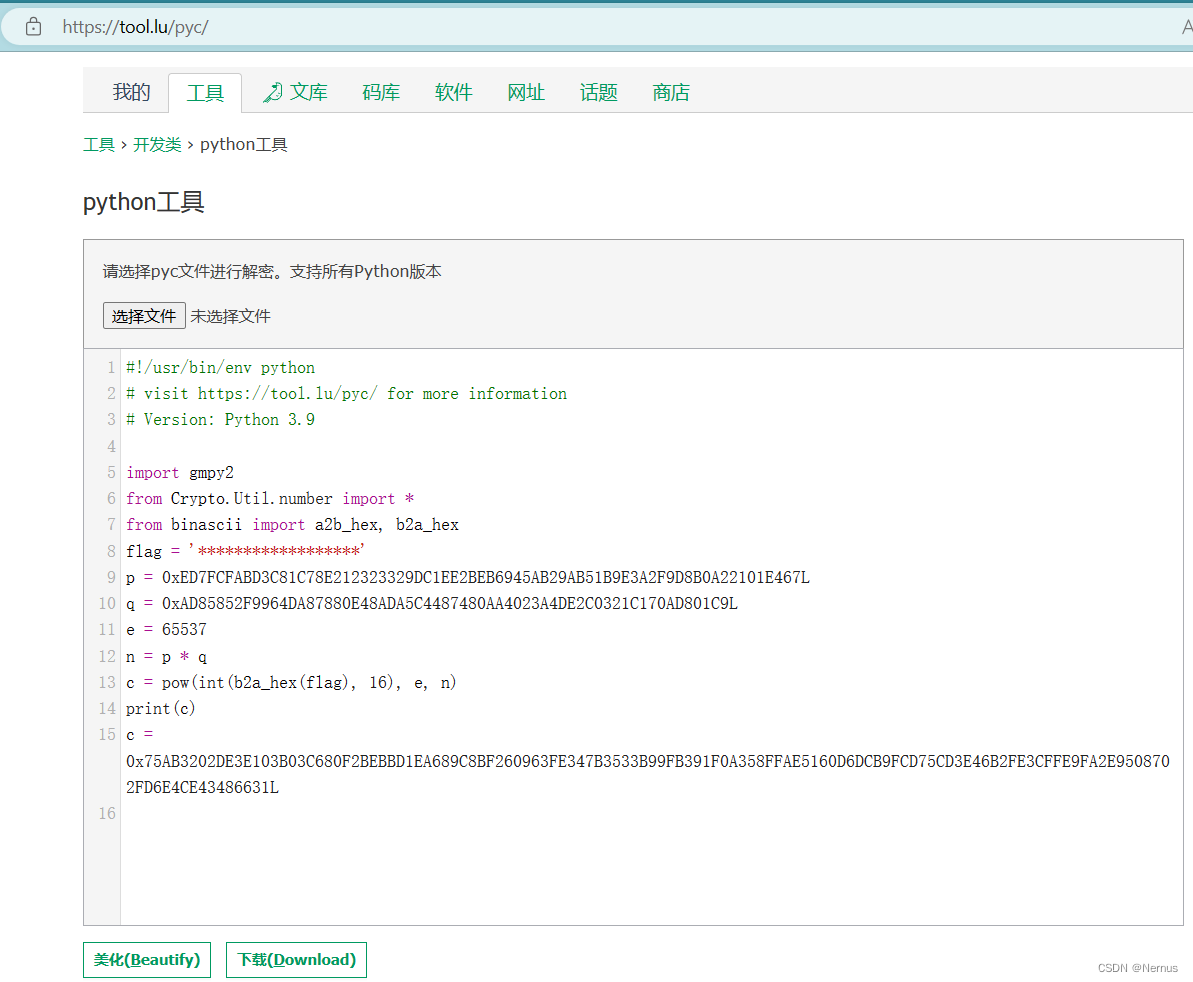
编译后,下载了一个压缩包文件,解压得到python代码
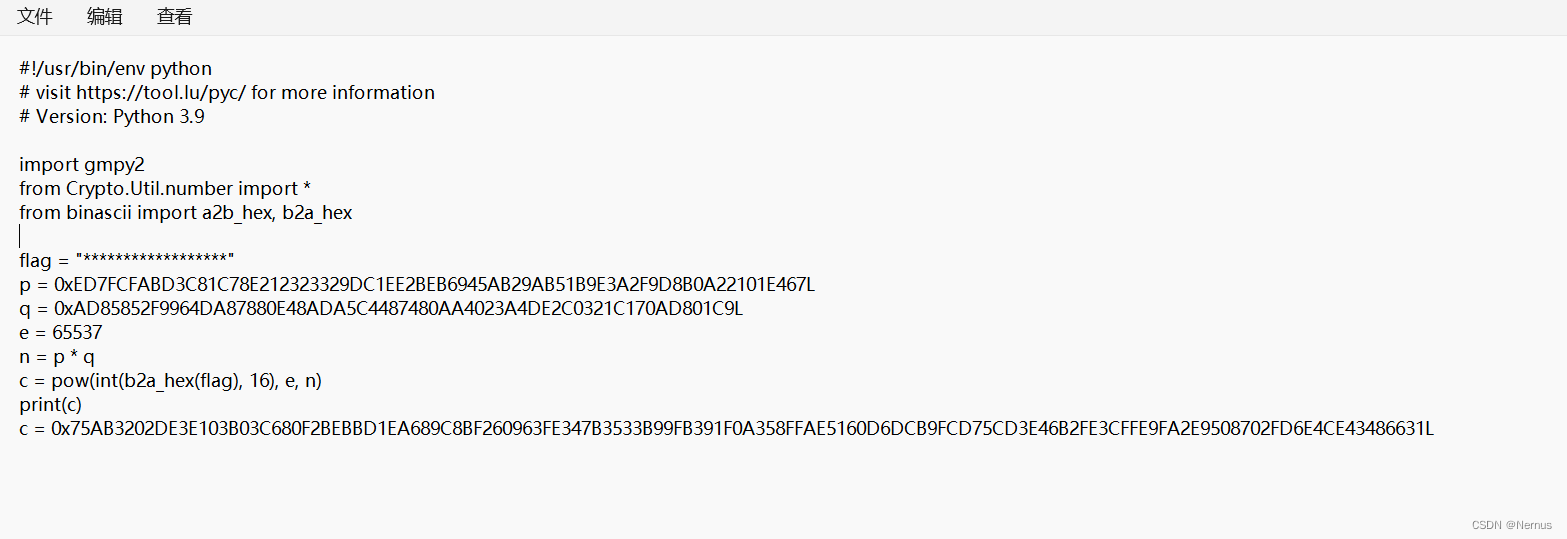
#!/usr/bin/env python
# visit https://tool.lu/pyc/ for more information
# Version: Python 3.9
import gmpy2
from Crypto.Util.number import *
from binascii import a2b_hex, b2a_hex
flag = "******************"
p = 0xED7FCFABD3C81C78E212323329DC1EE2BEB6945AB29AB51B9E3A2F9D8B0A22101E467L
q = 0xAD85852F9964DA87880E48ADA5C4487480AA4023A4DE2C0321C170AD801C9L
e = 65537
n = p * q
c = pow(int(b2a_hex(flag), 16), e, n)
print(c)
c = 0x75AB3202DE3E103B03C680F2BEBBD1EA689C8BF260963FE347B3533B99FB391F0A358FFAE5160D6DCB9FCD75CD3E46B2FE3CFFE9FA2E9508702FD6E4CE43486631L审计加密代码,已知p,q,e,n,c
m=c^d mod n 所以我们求出d即可解出明文
编写脚本
from Crypto.Util.number import *
import gmpy2
import base64
p = int("0xED7FCFABD3C81C78E212323329DC1EE2BEB6945AB29AB51B9E3A2F9D8B0A22101E467",16)
q = int("0xAD85852F9964DA87880E48ADA5C4487480AA4023A4DE2C0321C170AD801C9",16)
e = 65537
n = p * q
c = int("0x75AB3202DE3E103B03C680F2BEBBD1EA689C8BF260963FE347B3533B99FB391F0A358FFAE5160D6DCB9FCD75CD3E46B2FE3CFFE9FA2E9508702FD6E4CE43486631",16)
phi = (p-1)*(q-1) #求φ(n),φ(n)=(p-1)(q-1)
d = gmpy2.invert(e,phi) #求e对于模n的逆元,即解密指数d
m = pow(c,d,n) #m=c^e mod n,m为10进制格式
flag = long_to_bytes(m) #m的字符串形式
print(base64.b64decode(flag)) #上面得到的flag是base64编码,进行一次base64解码即可
运行脚本
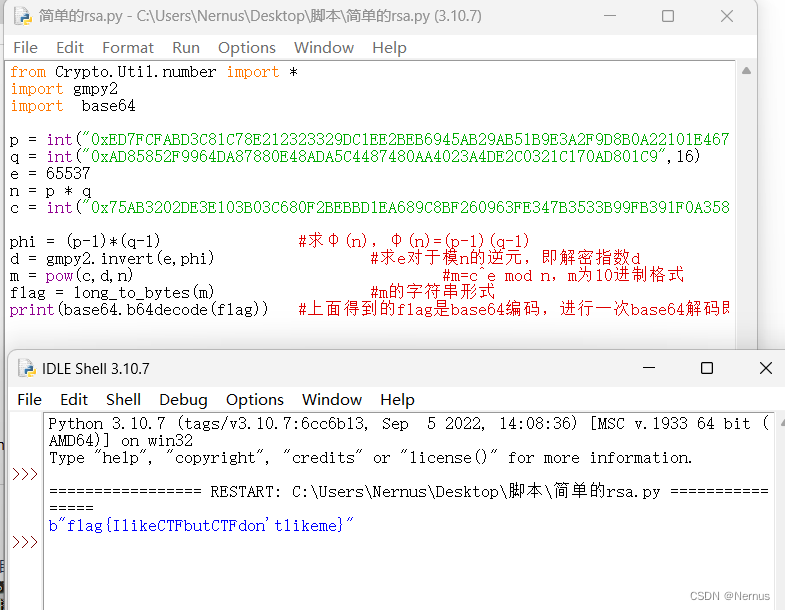
得到flag
托马斯.杰斐逊
下载打开附件
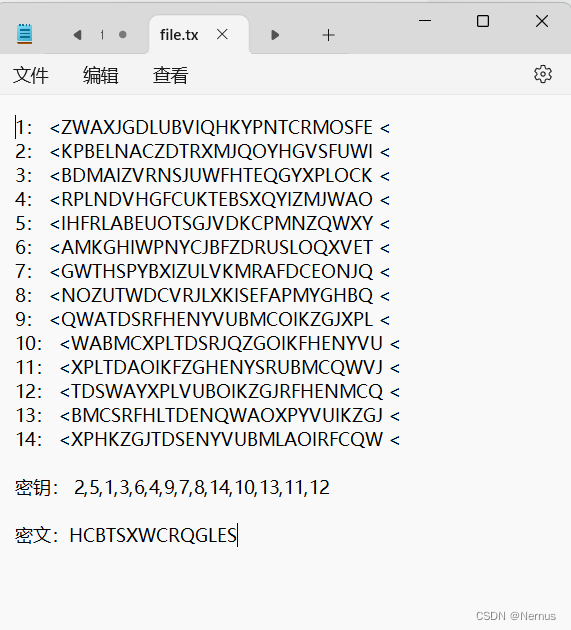
内容如下
1: <ZWAXJGDLUBVIQHKYPNTCRMOSFE <
2: <KPBELNACZDTRXMJQOYHGVSFUWI <
3: <BDMAIZVRNSJUWFHTEQGYXPLOCK <
4: <RPLNDVHGFCUKTEBSXQYIZMJWAO <
5: <IHFRLABEUOTSGJVDKCPMNZQWXY <
6: <AMKGHIWPNYCJBFZDRUSLOQXVET <
7: <GWTHSPYBXIZULVKMRAFDCEONJQ <
8: <NOZUTWDCVRJLXKISEFAPMYGHBQ <
9: <QWATDSRFHENYVUBMCOIKZGJXPL <
10: <WABMCXPLTDSRJQZGOIKFHENYVU <
11: <XPLTDAOIKFZGHENYSRUBMCQWVJ <
12: <TDSWAYXPLVUBOIKZGJRFHENMCQ <
13: <BMCSRFHLTDENQWAOXPYVUIKZGJ <
14: <XPHKZGJTDSENYVUBMLAOIRFCQW <密钥: 2,5,1,3,6,4,9,7,8,14,10,13,11,12
密文:HCBTSXWCRQGLES
这是一种加密方式,叫做轮转密码或者叫比尔密码,
解密的方式就是先通过密钥调整字符串的行号,然后通过密文调整每一行字符串的顺序

先人工将字符串行号排序,放到一个txt中

然后才用脚本解密,脚本如下:
fileone = open("1.txt","r+") #手工排序行号的字符串
filetwo = open("a.txt","w+") # 新的文件保存结果
attr = "HCBTSXWCRQGLES" # 密文
attrtwo = ""
num = 0
for line in fileone:
print(len(line))
for i in line:
if i != attr[num]:
attrtwo = attrtwo + i
else:
#attrtwo = attrtwo + i
attrone = line[len(attrtwo):26]+attrtwo + "\n"
filetwo.write(attrone)
break
attrtwo = ""
num = num + 1
fileone.close()
filetwo.close()
运行脚本时,1.txt内仅保留

运行脚本,得到a.txt文件

仔细观察每一列,在倒数第六列有发现:

得到:XSXSBUGKUADMIN
flag包裹提交后,提示flag错误
注意大小写区别,正确的flag为:
flag{xsxsbugkuadmin}
这不是md5
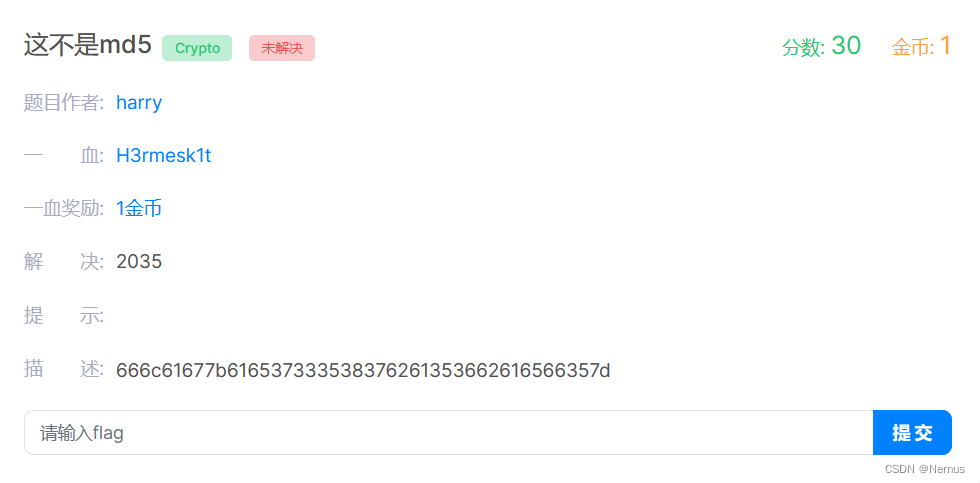
题目描述:666c61677b616537333538376261353662616566357d
16进制到文本字符串
使用在线工具16进制转换,16进制转换文本字符串,在线16进制转换 | 在线工具 (sojson.com)
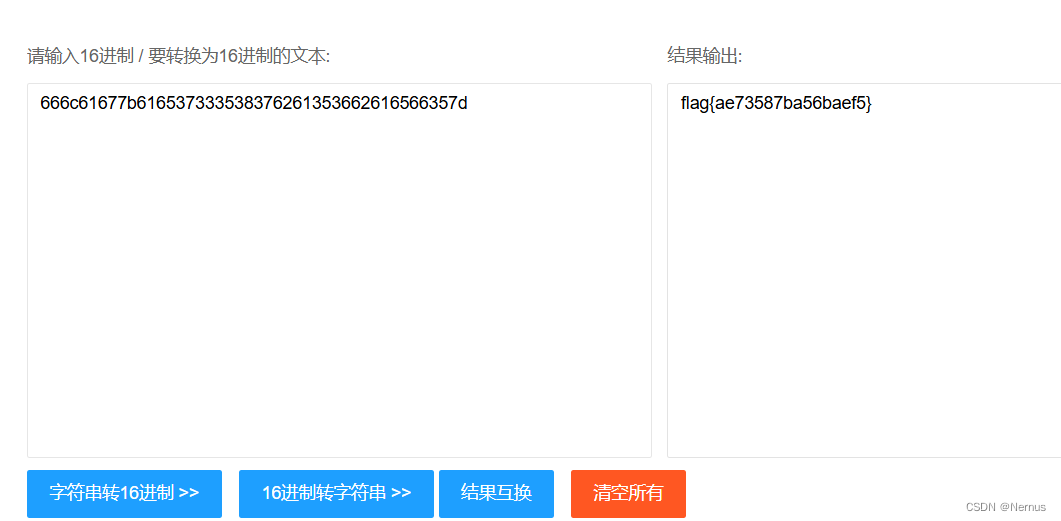
得到flag
进制转换
题目描述:二进制、八进制、十进制、十六进制,你能分的清吗?
下载附件,得到
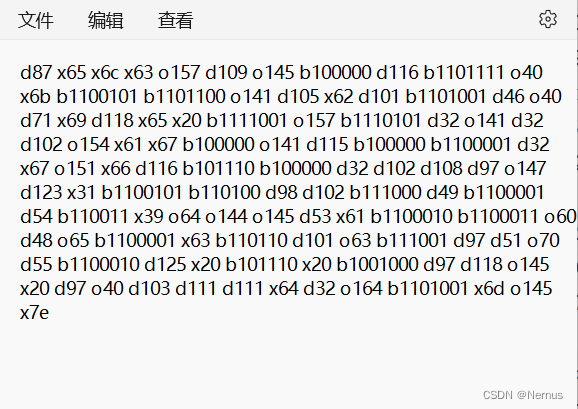
d87 x65 x6c x63 o157 d109 o145 b100000 d116 b1101111 o40 x6b b1100101 b1101100 o141 d105 x62 d101 b1101001 d46 o40 d71 x69 d118 x65 x20 b1111001 o157 b1110101 d32 o141 d32 d102 o154 x61 x67 b100000 o141 d115 b100000 b1100001 d32 x67 o151 x66 d116 b101110 b100000 d32 d102 d108 d97 o147 d123 x31 b1100101 b110100 d98 d102 b111000 d49 b1100001 d54 b110011 x39 o64 o144 o145 d53 x61 b1100010 b1100011 o60 d48 o65 b1100001 x63 b110110 d101 o63 b111001 d97 d51 o70 d55 b1100010 d125 x20 b101110 x20 b1001000 d97 d118 o145 x20 d97 o40 d103 d111 d111 x64 d32 o164 b1101001 x6d o145 x7e
大佬的一些说法

以及在线网站
CTF在线工具-ASCII与进制转换|任意进制转换|ASCII、2进制、8进制、10进制、16进制 (hiencode.com)
编写脚本
keystring = "d87 x65 x6c x63 o157 d109 o145 b100000 d116 b1101111 o40 x6b b1100101 b1101100 o141 d105 x62 d101 b1101001 d46 o40 d71 x69 d118 x65 x20 b1111001 o157 b1110101 d32 o141 d32 d102 o154 x61 x67 b100000 o141 d115 b100000 b1100001 d32 x67 o151 x66 d116 b101110 b100000 d32 d102 d108 d97 o147 d123 x31 b1100101 b110100 d98 d102 b111000 d49 b1100001 d54 b110011 x39 o64 o144 o145 d53 x61 b1100010 b1100011 o60 d48 o65 b1100001 x63 b110110 d101 o63 b111001 d97 d51 o70 d55 b1100010 d125 x20 b101110 x20 b1001000 d97 d118 o145 x20 d97 o40 d103 d111 d111 x64 d32 o164 b1101001 x6d o145 x7e"
keys = keystring.split(" ")
flag = ""
for k in keys:
if k[0] == "d":
flag += chr(int(k[1:], 10))
elif k[0] == "x":
flag += chr(int(k[1:], 16))
elif k[0] == "b":
flag += chr(int(k[1:], 2))
elif k[0] == "o":
flag += chr(int(k[1:], 8))
print("flag: %s" % flag)运行后得到flag
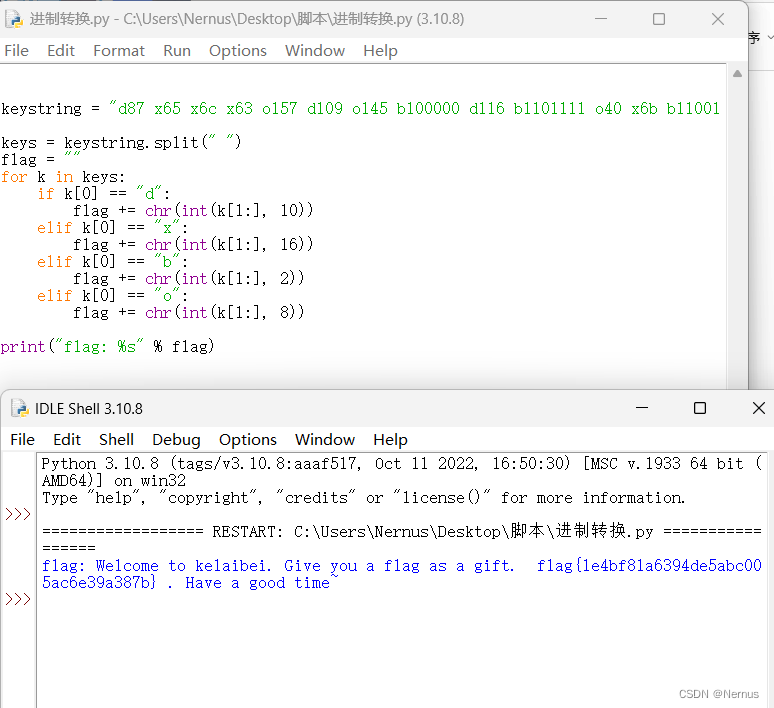
得到flag
affine
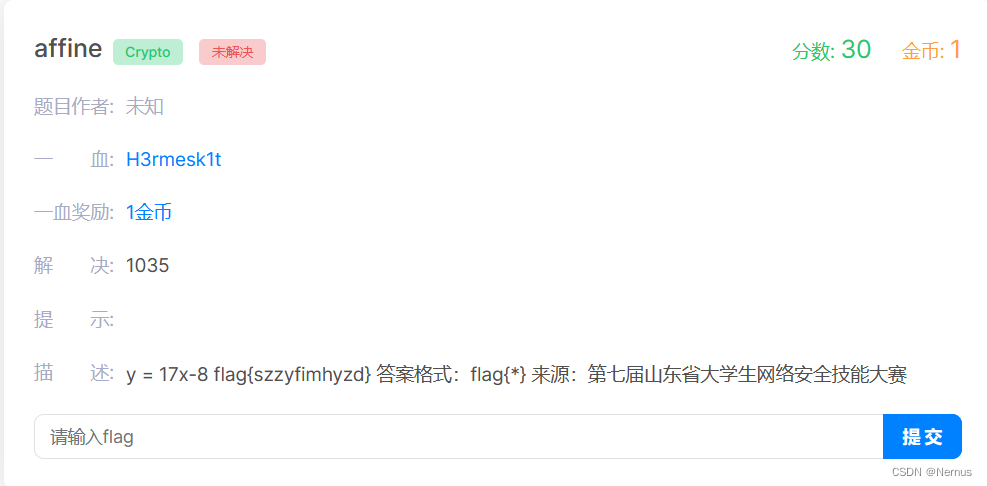
题目描述:
y = 17x-8 flag{szzyfimhyzd} 答案格式:flag{*}
BugkuCTF-Crypto题affine_ctfaffine-CSDN博客
搜索资料得:
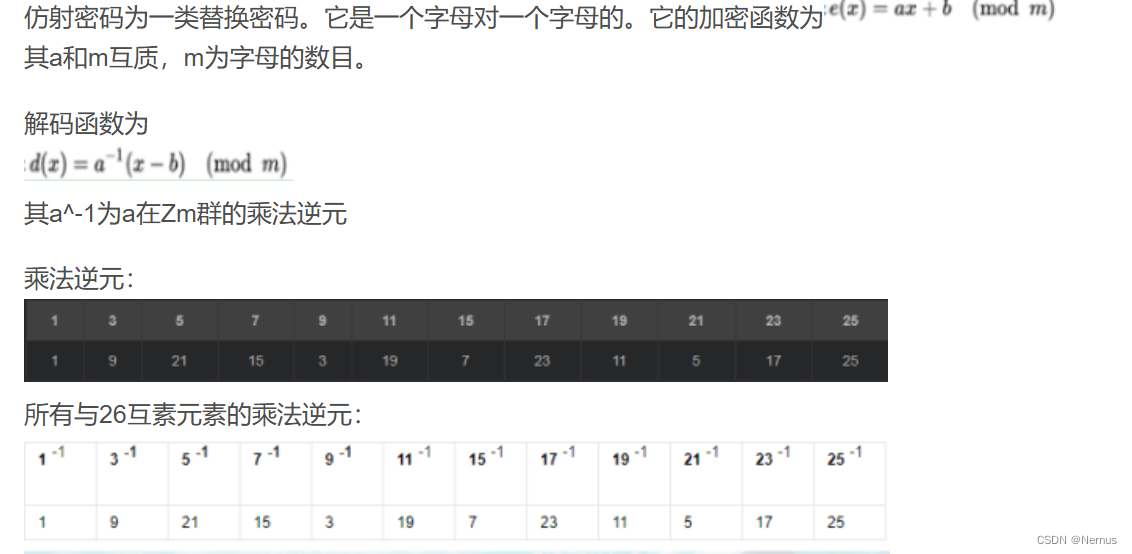
编写脚本,运行得到flag
方法一
#-*-coding:utf-8-*-
#i=1
#while(17*i%26!=1):
# i+=1
#求出17的乘法逆元
x='szzyfimhyzd'
for i in range(len(x)):
print(i,chr(23*(ord(x[i])-ord('a')+8)%26+ord('a')))
方法二
x='szzyfimhyzd'
for i in range(len(x)):
temp=23*(ord(x[i])-ord('a')+8)
temp=temp%26
result = temp + ord('a')
print(chr(result),end='')方法三
flag ="szzyfimhyzd"
flagList=[]
for i in flag:
flagList.append(ord(i)-97)
ansFlag = ""
for i in flagList:
for j in range(0, 26):
c=(17 * j - 8) % 26
if c==i:
ansFlag += chr(j+97)
ansFlag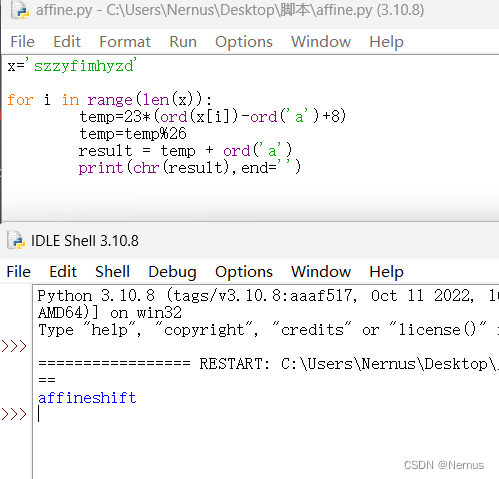
得到flag
flag{affineshift}
Crack it
下载附件,解压打开得到未知文件
他放到linux之中 ,在此处打开终端
使用命令查看文件
可以使用命令查看shadow文件信息。
more shadow
得到
root:$6$HRMJoyGA$26FIgg6CU0bGUOfqFB0Qo9AE2LRZxG8N3H.3BK8t49wGlYbkFbxVFtGOZqVI
q3qQ6k0oetDbn2aVzdhuVQ6US.:17770:0:99999:7:::
继续使用命令
john [OPTIONS] [PASSWORD-FILES]
john [选项] [密码文件]
--show[=LEFT] 显示破解的密码[如果=左,然后uncracked]
john --show shadow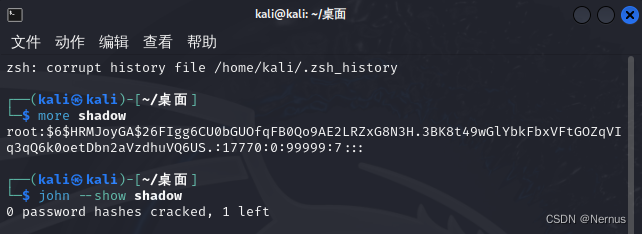
但是似乎解密失败了,尝试换一个命令
john shadow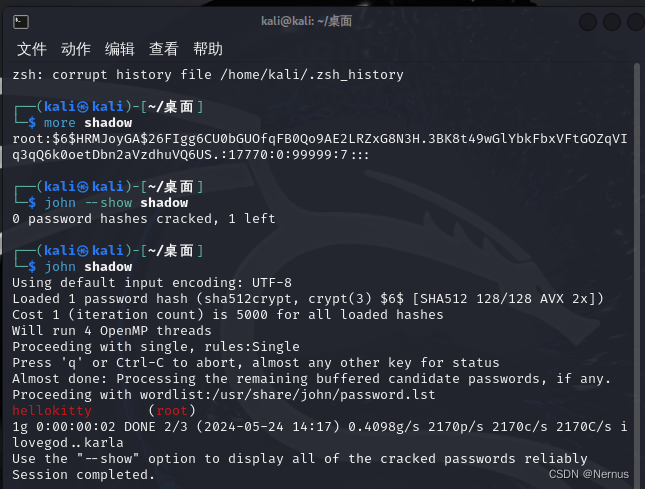
可以得到密码 hellokitty
按照提示,修改格式后,得到flag
flag{hellokitty}
rsa
下载附件,得到如下内容
N : 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597
e : 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619enc : 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
采用factordb分解N,得到p,q。factordb.com
p = 15991846970993213322072626901560749932686325766403404864023341810735319249066370916090640926219079368845510444031400322229147771682961132420481897362843199
q = 28805791771260259486856902729020438686670354441296247148207862836064657849735343618207098163901787287368569768472521344635567334299356760080507454640207003
计算:
phi = (p - 1) * (q - 1)
d = invmod(e, N)
恢复明文:
m = pow(enc, d, N) % N
编写python脚本
import gmpy2
from Crypto.Util.number import long_to_bytes
N = 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619
enc = 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
p = 15991846970993213322072626901560749932686325766403404864023341810735319249066370916090640926219079368845510444031400322229147771682961132420481897362843199
q = 28805791771260259486856902729020438686670354441296247148207862836064657849735343618207098163901787287368569768472521344635567334299356760080507454640207003
phi = gmpy2.mul(p - 1, q - 1)
d = gmpy2.invert(e, phi)
m = pow(enc, d, N) % N
print(long_to_bytes(m))运行
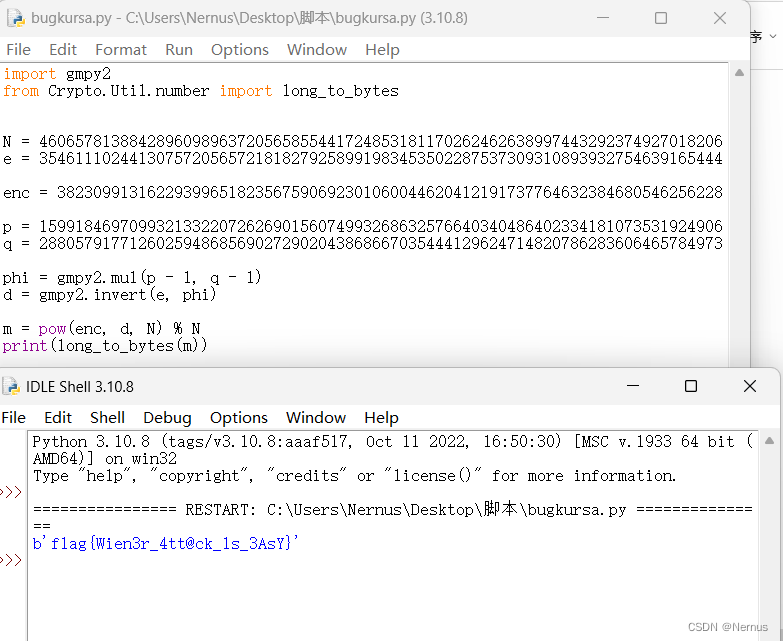
得到flag