---

题目

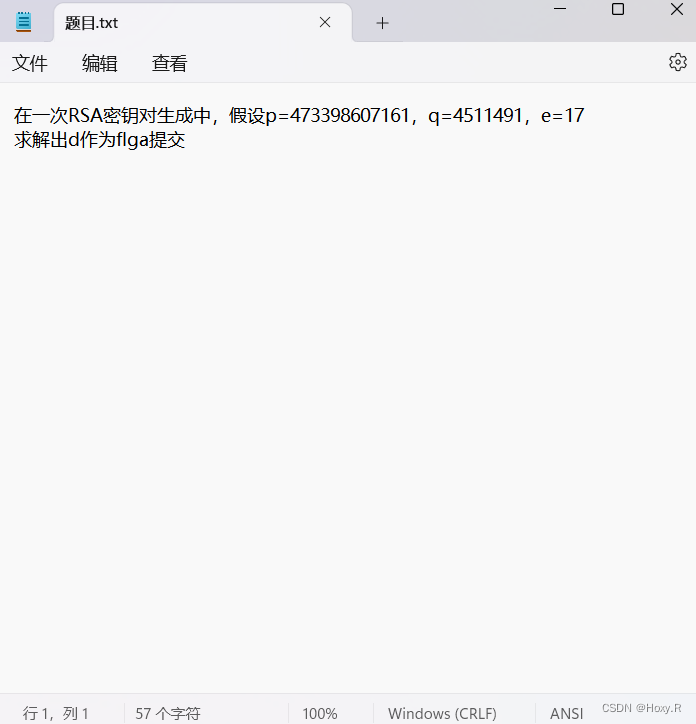
p=473398607161
q=4511491
e=17
求d

步骤

1.计算 𝑛

公式：n=p×q

n=473398607161×4511491=2135733555619387051

2.计算欧拉函数 𝜙(𝑛)

公式：𝜙(𝑛)=(p−1)×(q−1)

𝜙(𝑛)=(473398607161−1)×(4511491−1)=2135733082216268400

3. 扩展欧几里得算法求逆元 𝑑

d×e≡1(mod𝜙(𝑛))
意思是在模 𝜙(𝑛)的运算下，𝑑和𝑒是互为乘法逆元的。也就是说𝑑是𝑒的逆元，使得𝑒乘以𝑑后对𝜙(𝑛) 取模得到 1

直接用python进行计算

from sympy import mod_inverse

# 给定值
e = 17
phi_n = 2135732641062828400

# 计算 d (e 在模 phi_n 下的乘法逆元)
d = mod_inverse(e, phi_n)
print(d)  # 输出应为 125631357777427553

其实直接可以所有计算都交给python

from sympy import mod_inverse
p = 473398607161
q = 4511491
e = 17
phi_n = (p - 1) * (q - 1)
d = mod_inverse(e, phi_n)
print(d)

---

解题感悟

手撕这道题的话需要用到：扩展欧几里得算法，欧拉函数，模运算，逆元的求解等…感受到了python的便利!