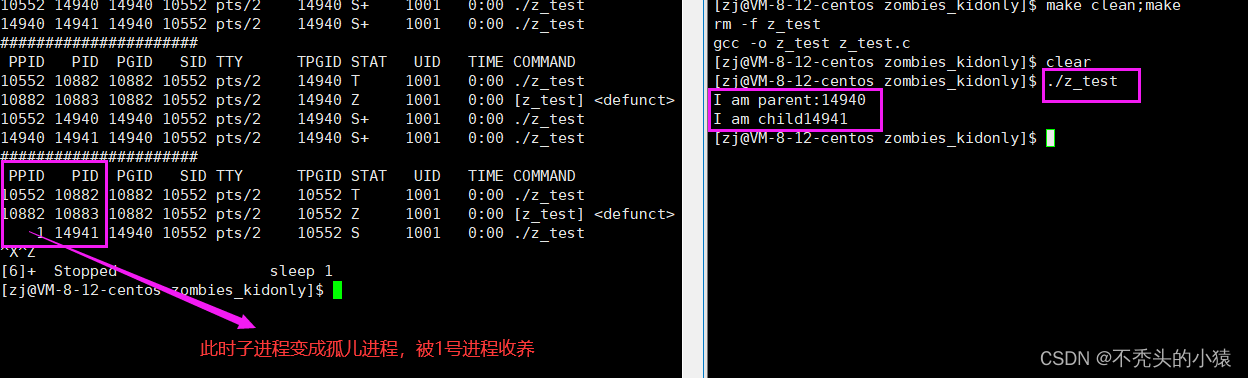
子空间投影

	从向量的投影入手，延伸到高维投影，并将投影使用矩阵形式给出。做投影也即向另一个向量上做垂线。上一章讨论的Ax=b无解时的最优解求解时，并没有解释这个最优解为何“最优”，本节课给出相应的解释。

相对简单的二维空间的投影

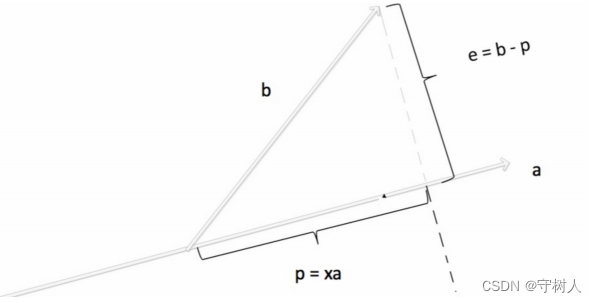
如上图，p也即向量a在向量上的投影，p在向量a上，是a的倍数，故令p=xa 。将b与p的差
设为e，带有误差的意思，同时e的模在某种程度上表示了b到a的最短距离（而这正是最优的体
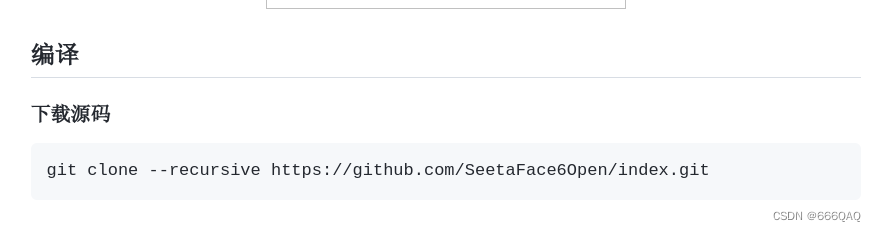
现：误差最小）。 e与 a正交。
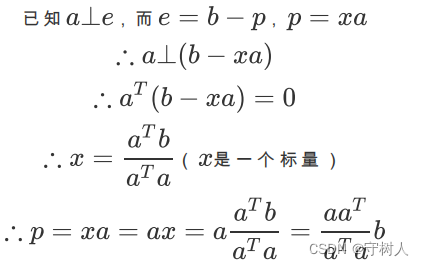注意， 其中的 aTa 是一个标量，而 aaT是一个矩阵。假设b变为原来的 2倍，那么显然投影p 也变为原来的 2倍。但如果a变为原来的 2 倍，整个aaT/aTa并没有发生变化，所以投影 p 不变。

令P = aaT/aTa，则有p = Pb，将P称为投影矩阵，则当向量与P相乘后，即可得到向量对应得到a上的投影。

投影矩阵的性质：
（1）rank（p）= 1
（2）向量 是 的列空间的基，向量 所在的直线是 的列空间。
（3）P是对称的。
（4）P2 = P。因为给定向量 ，对其进行一次 投影和对其进行两次投影，结果相同。

最小二乘法初涉

如图，要求找到一条最优的直线来拟合图中的三个点

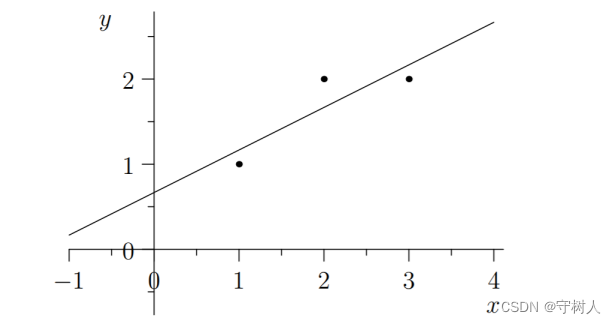
假设最优直线方程为C+Dt = b ，代入三个点(1,1),(2,2),(3,2) 可得方程组：

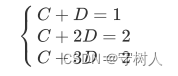
写作矩阵形式有：

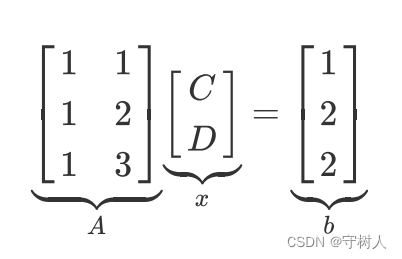
显然方程组无解，但有解（ 的各列线性无关），而 也是最小二乘法的核心方程