一、前言

本文主要讲了剪枝的概念、类别与DFS的一些例题。

二、剪枝

1、概念

剪枝：把不会产生答案的，或不必要的枝条“剪掉”。

剪枝的关键：剪什么枝、在哪里减。

剪枝是搜索常用的优化手段，常常能把指数级的复杂度，优化到近似多项式的复杂度。

2、类别

可行性剪枝：对当前状态进行检查，如果当前条件不合法就不再继续，直接返回。
搜索顺序剪枝：搜索树有多个层次和分支，不同的搜索顺序会产生不同的搜索树形态。
最优性剪枝：在最优化问题的搜索过程中，如果当前花费的代价已超过前面搜索到的最优解，那么本次搜索已经没有继续进行下去的意义，停止对当前分支的搜索。
排除等效冗余：搜索的不同分支，最后的结果是一样的，那么只搜一个分支就够了。
记忆化搜索：在递归的过程中，有许多分支被反复计算，会大大降低算法的执行效率。将已经计算出来的结果保存起来，以后需要用到的时候直接取出结果，避免重复运算，从而提高了算法的效率。

三、例题

1、剪格子（lanqiaoOJ题号211）

【题目描述】

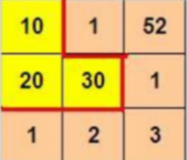
如下图所示，3×3 的格子中填写了一些整数。

沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 60。请你编程判定：对给定的 m×n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。无法分割输出 0。

【输入描述】

第一行是 2 个整数 m，n，表示表格的宽度和高度。后面 n 行，每行 m 个正整数。

【输出描述】

在所有解中，包含左上角的分割区可能包含的最小的格子数目。

这是一道典型的 DFS 题。

思路：先求所有格子的和 sum，然后用 DFS 找一个联通区域，看这个区域的和是否为 sum/2。
剪枝：如果 DFS 到的部分区域的和已经超过 sum/2，就不用继续 DFS 了。
这种格子DFS搜索题，是蓝桥杯的常见考题。

def dfs(x,y,c,s):
    global sum_num,ans
    if 2*s>sum_num:     #剪枝
        return
    if 2*s==sum_num:    #终止条件
        if ans>c and vis[0][0]==1:
            ans=c
        return
    vis[x][y]=1         #保存现场
    dir=[(1,0),(-1,0),(0,-1),(0,1)]
    for u,v in dir:     #遍历
        tx,ty=x+u,y+v
        if tx>=0 and tx<=n-1 and ty>=0 and ty<=m-1:
            if vis[tx][ty]==0:
                dfs(tx,ty,c+1,s+a[x][y])
    vis[x][y]=0         #恢复现场
    
m,n=map(int,input().split())
a=[list(map(int,input().split())) for _ in range(n)]    #输入矩阵
vis=[[0]*m for _ in range(n)]
sum_num=0
for i in a:
    sum_num+=sum(i)
ans=1000000
dfs(0,0,0,0)
print(ans)

2、路径之谜（2016年决赛，lanqiaoOJ题号89）

【题目描述】

小明冒充骑士进入了一个城堡。城堡里边方形石头铺成的地面。假设城堡地面是 n×n 个方格。按习俗，骑士要从西北角走到东南角。可以横向或纵向移动，但不能斜着走，也不能跳跃。每走到一个新方格，就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有 n 个靶子) 同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？

本题的要求就是已知箭靶数字，求骑士的行走路径 (测试数据保证路径唯一)

【输入格式】

第一行一个整数 N (0<N<20)，表示地面有 N×N 个方格；第二行 N 个整数，空格分开，表示北边的箭靶上的数字 (自西向东)；第三行 N 个整数，空格分开，表示西边的箭靶上的数字 (自北向南)。

【输出格式】

一行若干个整数，表示骑士路径。为了方便表示，我们约定每个小格子用一个数字代表，从西北角 (左上角) 开始编号：0,1,2,3 ....

【输入示例】

4

2 4 3 4

4 3 3 3

【输出示例】

0 4 5 1 2 3 7 11 10 9 13 14 15

DFS：题目要求输出一条路径，用 DFS 很合适, DFS 搜索过程中，自然生成一条路径。

剪枝：每走到一个格子，对应的靶子上箭多一支，靶子上的箭等于给定的数字后，就不用再 DFS 下去了。(或者做减法，靶子的数字减到 0)

记录路径的技巧。根据题目的要求，用栈来跟踪DFS的过程，记录DFS走过的路径，是最方便的。DFS到某个格子时，把这个格子放到栈里，表示路径增加了这个格子。DFS 回溯的时候，退出了这个格子，表示路径上不再包括这个格子，需要从栈中弹走这个格子。

def dfs(x,y):
    if a[x]<0 or b[y]<0:    #剪枝：数字减到0
        return
    if x==n-1 and y==n-1:   #终止条件：到达终点
        ok=1
        for i in range(n):
            if a[i]!=0 or b[i]!=0:
                ok=0
                return
        if ok==1:           #成功找出路径并输出
            for i in range(len(path)):
                print(path[i],end=' ')
    for u,v in [(1,0),(-1,0),(0,1),(0,-1)]:     #遍历
        tx,ty=x+u,y+v
        if 0<=tx<n and 0<=ty<n and vis[tx][ty]==0:
            vis[tx][ty]=1
            path.apppend(tx*n+ty)   #进栈，记录路径
            a[tx]-=1                #根据题意，这里箭数要减 1
            b[ty]-=1
            dfs(tx,ty)
            path.pop()              #出栈，DFS回溯
            a[tx]+=1
            b[ty]+=1
            vis[tx][ty]=0
            
n=int(input())
vis=[[0]*n for i in range(n)]
path=[]     #用栈记录路径
path.appendd(0)
b=list(map(int,input().split()))    #输入北边和西边的靶子
a=list(map(int,input().split()))
vis[0][0]=1
a[0]-=1
b[0]-=1     #从左上角出发
dfs(0,0)

3、四阶幻方（2015年决赛，lanqiaoOJ题号689）

【题目描述】

把 1～16 的数字填入 4×4 的方格中，使得行、列以及两个对角线的和都相等，满足这样的特征时称为：四阶幻方。

四阶幻方可能有很多方案。如果固定左上角为 1，请计算一共有多少种方案。

除了 1，数字 2~16 有 15! = 1.3×10^12 种排列，无法把所有排列都试一遍。

剪枝：每种排列，只要前面一些数字不适合，就不用再计算下去了。

需要自写排列。

def dfs(n):
    global cnt
    if n>=4 and m[0]+m[1]+m[2]+m[3]!=34:
        return
    if n>=7 and m[0]+m[4]+m[5]+m[6]!=34:
        return
    if n>=10 and m[1]+m[7]+m[8]+m[9]!=34:
        return
    if n>=11 and m[3]+m[6]+m[8]+m[10]!=34:
        return
    if n>=12 and m[4]+m[7]+m[10]+m[11]!=34:
        return
    if n>=14 and m[5]+m[8]+m[12]+m[13]!=34:
        return
    if n>=15 and m[2]+m[10]+m[12]+m[14]!=34:
        return
    if n>=16 and (m[6]+m[9]+m[14]+m[15]!=34 \
                  or m[3]+m[11]+m[13]+m[15]!=34 \
                  or m[0]+m[7]+m[12]+m[15]!=34):
        return      #上面所有的条件判断都是剪枝
    if n==16:
        cnt+=1
    for i in range(2,17):   #2~16的全排列
        if vis[i]==0:
            m[n]=i
            vis[i]=1
            dfs(n+1)
            vis[i]=0

cnt=0
m=[0]*17    #用一维数组表示幻方
m[0]=1      # 1 被固定
vis=[0]*17
vis[1]=1
dfs(1)
print(cnt)

4、分考场（2017年决赛，lanqiaoOJ题号109）

【题目描述】

n 个人参加考试。为了公平，要求任何两个认识的人不能分在同一个考场。求最少需要分几个考场才能满足条件。

【输入格式】

第一行，一个整数 n (1<n<100)，表示参加考试的人数。

第二行，一个整数 m，表示接下来有 m 行数据。以下 m 行每行的格式为：两个整数 a, b，用空格分开 (1<=a, b<=n) 表示第 a 个人与第 b 个人认识（编号从1开始）。

【输出格式】

一行一个整数，表示最少分几个考场。

【输入】

5

8

1 2

1 3

1 4

2 3

2 4

2 5

3 4

4 5

【输出】

4

【思路】

从第 1 个考场开始，逐个加入考生。每新加进来一个人 x，都与已经开设的考场里面的人进行对比，如果认识，就换个考场。直到找到一个考场，考场里面所有的人都不认识x，x就可以坐在这里。如果所有已经开设的考场都有熟人，就开一个新考场给 x 坐。
这个模拟的结果是得到了一个可行的考场安排，但这个安排的考场数量不一定是最少的。
题目求最少考场数量，需要把所有可能的考场安排都暴力地试一遍，找到最少的那个考场安排。

用 DFS 搜索所有可能的情况，得到最少考场。暴力搜索所有的考场安排，计算量很大。
剪枝：用剪枝来减少搜索。在搜索一种新的可能的考场安排时，如果需要的考场数量已经超过了原来某个可行的考场安排，就停止。

def dfs(x,room):
    global num,p
    if room>num:    #剪枝: 需要的考场数量已经超过了原来某个可行的考场安排，停止
        return
    if x>n:         #终止条件
        if room<num:
            num=room
        return
    for j in range(1,room+1):   #遍历
        k=0
        while p[j][k] and a[x][p[j][k]]==0:
            k+=1
        if p[j][k]==0:
            p[j][k]=x
            dfs(x+1,room)
            p[j][k]=0
    p[room+1][0]=x
    dfs(x+1,room+1)
    p[room+1][0]=0

n=int(input())
m=int(input())
num=110
p=[[0 for i in range(n+1)] for j in range(n+1)]
a=[[0 for i in range(n+1)] for j in range(n+1)]
for i in range(m):
    u,v=map(int,input().split())
    a[u][v]=a[v][u]=1
dfs(1,0)
print(num)