题目

[NOIP2001 普及组] 数的计算

题目描述

给出自然数 $n$，要求按如下方式构造数列：

1. 只有一个数字 $n$ 的数列是一个合法的数列。
2. 在一个合法的数列的末尾加入一个自然数，但是这个自然数不能超过该数列最后一项的一半，可以得到一个新的合法数列。

请你求出，一共有多少个合法的数列。两个合法数列 $a,b$ 不同当且仅当两数列长度不同或存在一个正整数 $i\le |a|$，使得 $a_i\ne b_i$。

输入格式

输入只有一行一个整数，表示 $n$。

输出格式

输出一行一个整数，表示合法的数列个数。

样例 #1

样例输入 #1

6

样例输出 #1

6

提示

样例 1 解释

满足条件的数列为：

• $6$
• $6,1$
• $6,2$
• $6,3$
• $6,2,1$
• $6,3,1$

数据规模与约定

对于全部的测试点，保证 $1\le n\le 10^3$。

说明

本题数据来源是 NOIP 2001 普及组第一题，但是原题的题面描述和数据不符，故对题面进行了修改，使之符合数据。原题面如下，谨供参考：

我们要求找出具有下列性质数的个数（包含输入的正整数 $n$）。

先输入一个正整数 $n$（$n\le 1000$），然后对此正整数按照如下方法进行处理：

1. 不作任何处理；
2. 在它的左边拼接一个正整数，但该正整数不能超过原数，或者是上一个被拼接的数的一半；
3. 加上数后，继续按此规则进行处理，直到不能再加正整数为止。

感谢 @dbxxx 对本题情况的反馈，原题面的问题见本贴。

解题思路

• 递推公式。
• 设定一个数组f[n]表示数字n的答案。

函数	答案
f[1]	1
f[2]	2
f[3]	2
f[4]	4
f[5]	4
f[6]	6
f[7]	6
f[8]	10
f[9]	10
f[10]	14

• 所以我们可以得出规律，当n为奇数时，f[n] = f[n - 1];当n为偶数时，f[n] = f[n - 1] + f[n / 2]

Code

#include <iostream>

using namespace std;

int main() {
	int f[10005];
	int t;
	int ans = 0;
	cin >> t;  // 输入数据
	f[1] = 1;
	f[2] = 2;
	for (int i = 3; i <= t; i++) {
		f[i] = (i % 2 == 1) ? f[i - 1] : f[i - 1] + f[i / 2];
	}
	cout << f[t] << endl;
	return 0;
}

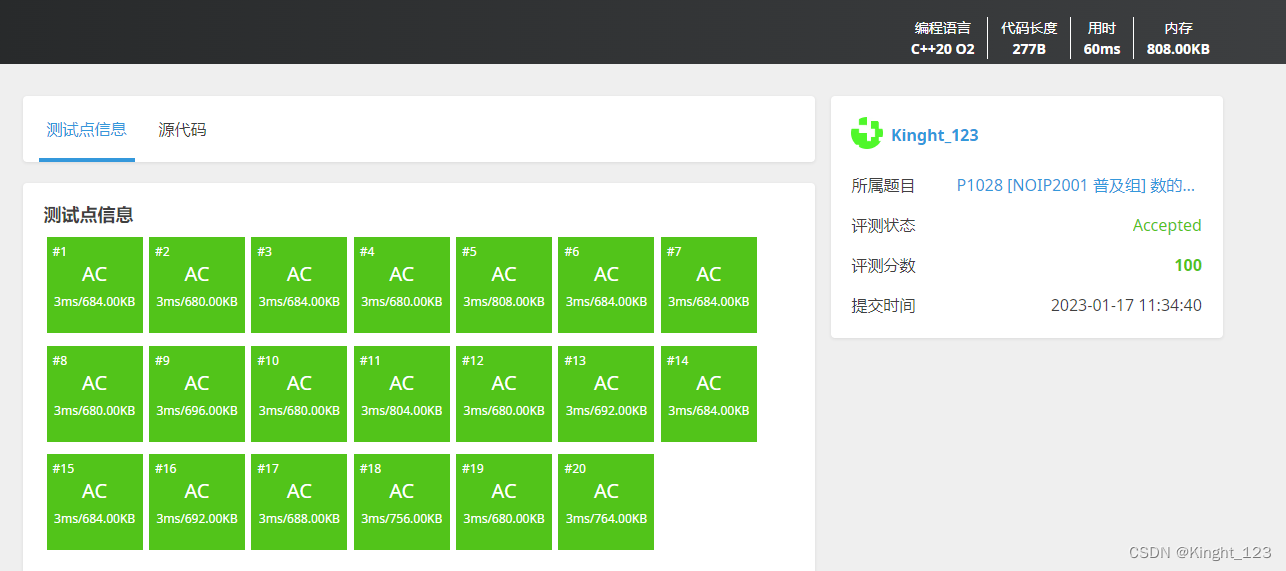
运行结果