0 核心框架汇总
框架思维
数据结构的存储方式只有两种:数组(顺序存储)和链表(链式存储)
算法
数学中的算法重在推导,计算机中的算法重在穷举
计算机算法的本质特点: 穷举
穷举有两个关键难点:无遗漏、无冗余
算法技巧
双指针解决单链表问题
public class ListNodePractice {
/**
* 876 给定一个头结点为 head 的非空单链表,返回链表的中间结点。
*
* 如果有两个中间结点,则返回第二个中间结点。
*
* 示例 1:
*
* 输入:[1,2,3,4,5]
* 输出:此列表中的结点 3 (序列化形式:[3,4,5])
* 返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
* 注意,我们返回了一个 ListNode 类型的对象 ans,这样:
* ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
* 示例 2:
*
* 输入:[1,2,3,4,5,6]
* 输出:此列表中的结点 4 (序列化形式:[4,5,6])
* 由于该列表有两个中间结点,值分别为 3 和 4,我们返回第二个结点。
* 提示:
*
* 给定链表的结点数介于 1 和 100 之间。
* @param head
* @return
*/
ListNode middleNode(ListNode head) {
// 快慢指针初始化指向 head
ListNode slow = head, fast = head;
// 快指针走到末尾时停止
while (fast != null && fast.next != null) {
// 慢指针走一步,快指针走两步
slow = slow.next;
fast = fast.next.next;
}
// 慢指针指向中点
return slow;
}
/**
* 剑指 Offer 18. 删除链表的节点
* 给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
*
* 返回删除后的链表的头节点。
*
* 注意:此题对比原题有改动
*
* 示例 1:
*
* 输入: head = [4,5,1,9], val = 5
* 输出: [4,1,9]
* 解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
*
* 说明:
*
* 题目保证链表中节点的值互不相同
* 若使用 C 或 C++ 语言,你不需要 free 或 delete 被删除的节点
* @param head
* @param val
* @return
*/
public ListNode deleteNode(ListNode head, int val) {
if(head == null) {
return null;
}
ListNode cur = head, pre = null;
while(cur != null) {
if(cur.val == val) {
if(cur.val == head.val) {
//删除头节点
return head.next;
} else {
//删除非头节点
pre.next = cur.next;
return head;
}
}
pre = cur;
cur = cur.next;
}
return head;
}
/**
* 如果链表中含有环,如何计算这个环的起点?
* @param head
* @return
*/
ListNode detectCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;
}
// 上面的代码类似 hasCycle 函数
if (fast == null || fast.next == null) {
// fast 遇到空指针说明没有环
return null;
}
// 重新指向头结点
slow = head;
// 快慢指针同步前进,相交点就是环起点
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
/**
* 剑指 Offer 22. 链表中倒数第k个节点
* 输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
*
* 例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
*
*
*
* 示例:
*
* 给定一个链表: 1->2->3->4->5, 和 k = 2.
*
* 返回链表 4->5.
* @param head
* @param k
* @return
*/
public ListNode getKthFromEnd(ListNode head, int k) {
if(head == null || k <= 0) {
return null;
}
ListNode cur = head;
List<ListNode> nodeList = new ArrayList<>();
while(cur != null) {
nodeList.add(cur);
cur = cur.next;
}
if(k > nodeList.size()) {
return null;
}
ListNode result = nodeList.get(nodeList.size() - k);
return result;
}
/**
* 剑指 Offer 25. 合并两个排序的链表
* 输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
*
* 示例1:
*
* 输入:1->2->4, 1->3->4
* 输出:1->1->2->3->4->4
* 限制:
*
* 0 <= 链表长度 <= 1000
* @param l1
* @param l2
* @return
*/
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1 == null) {
return l2;
}
if(l2 == null) {
return l1;
}
ListNode result = new ListNode(0);
ListNode resultTail = result;
while(l1 != null || l2 != null) {
if(l1 == null) {
resultTail.next = l2;
break;
}
if(l2 == null) {
resultTail.next = l1;
break;
}
if(l1.val <= l2.val) {
resultTail.next = l1;
l1 = l1.next;
} else {
resultTail.next = l2;
l2 = l2.next;
}
//先修改l1 l2,相当于抛弃之前的节点
resultTail = resultTail.next;
}
return result.next;
}
/**
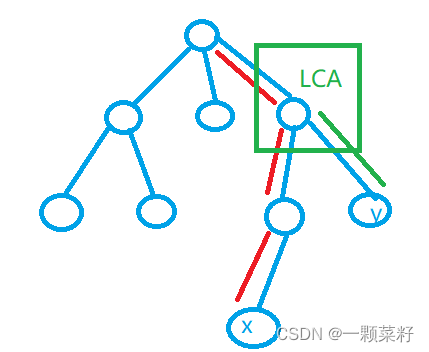
* 剑指 Offer 52. 两个链表的第一个公共节点
* 输入两个链表,找出它们的第一个公共节点。
*
* 如下面的两个链表:
*
* 在节点 c1 开始相交。
* @param headA
* @param headB
* @return
*/
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
//从两个链表的尾部,倒序,走相同距离后会到相交点
if(headA == null || headB == null) {
return null;
}
ListNode curA = headA, curB = headB;
List<ListNode> listA = new ArrayList<>();
List<ListNode> listB = new ArrayList<>();
while(curA != null) {
listA.add(curA);
curA = curA.next;
}
while(curB != null) {
listB.add(curB);
curB = curB.next;
}
ListNode result = null;
for (int i = listA.size() - 1, j = listB.size() - 1; i >= 0 && j >= 0; i--, j--) {
ListNode node = listA.get(i);
if(node == listB.get(j)) {
result = node;
}
}
return result;
}
/**
* 两个链表A, B;公共节点可以从两个链表的尾节点逆向比较,容易获取,但由于是单项链表,只能顺序访问。
* 所以可以考虑,将两个链表连接到一起,遍历两个链表,遇到的第一个相同公共节点就是公共节点的地址,如果一直没遇到,则为null
* @param headA
* @param headB
* @return
*/
public ListNode getIntersectionNode2(ListNode headA, ListNode headB) {
if(headA == null || headB == null) {
return null;
}
ListNode curA = headA, curB = headB;
while(curA != curB) {
//A链表向前走,走到末尾后走B
curA = curA == null ? headB: curA.next;
//B链表向前走,走到末尾后走A
curB = curB == null ? headA: curB.next;
}
return curA;
}
/**
* 剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
* 输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数在数组的前半部分,所有偶数在数组的后半部分。
* 示例:
*
* 输入:nums = [1,2,3,4]
* 输出:[1,3,2,4]
* 注:[3,1,2,4] 也是正确的答案之一。
* @param nums
* @return
*/
public int[] exchange(int[] nums) {
if(nums == null || nums.length == 0) {
return nums;
}
//双指针法
int i = 0, j = nums.length -1;
while (i < j) {
while (i < j && (nums[i] & 1) == 1) {
//奇数,指针后移
i++;
}
while (i < j && (nums[j] & 1) == 0) {
j--;
}
//交换数据
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
return nums;
}
/**
* 剑指 Offer 57. 和为s的两个数字
* 输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。
* 示例 1:
*
* 输入:nums = [2,7,11,15], target = 9
* 输出:[2,7] 或者 [7,2]
*
* 1 <= nums.length <= 10^5
* 1 <= nums[i] <= 10^6
* @param nums
* @param target
* @return
*/
public int[] twoSum(int[] nums, int target) {
if(nums == null || nums.length == 0) {
return null;
}
//hash保存,然后遍历时判断即可
Set<Integer> set = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
int a = nums[i];
if(a < target ) {
if(set.contains(target - a)) {
return new int[]{a, target - a};
}
set.add(a);
} else {
return null;
}
}
return null;
}
/**
* 由于数组是递增排序的,可以考虑折半查询<target的最大值,然后,两方
* @param nums
* @param target
* @return
*
*/
public int[] twoSum2(int[] nums, int target) {
if(nums == null || nums.length == 0) {
return null;
}
int i= 0, j = nums.length - 1;
while (i < j) {
int a = nums[i];
int b = nums[j];
int c = a + b;
if(c == target) {
return new int[]{a, b};
} else if(c > target) {
j--;
} else {
i++;
}
}
return null;
}
/**
* 双指针 + 折半
* @param nums
* @param target
* @return
*/
public int[] twoSum3(int[] nums, int target) {
if(nums == null || nums.length == 0) {
return null;
}
//查询<target的最大值坐标【不要求绝对精确,确定大致大致范围即可】,作为右指针的起始点
int left = 0, right = nums.length - 1, mid = 0;
int p = 0;
while (left < right) {
mid = (right - left >> 1) + left;
if(nums[mid] == target) {
break;
} else if(nums[mid] > target) {
//p在左侧
right = mid - 1;
} else {
//p在右侧
left = mid + 1;
}
}
p = mid + 1;
//双指针
int i= 0, j = p;
while (i < j) {
int a = nums[i];
int b = nums[j];
int c = a + b;
if(c == target) {
return new int[]{a, b};
} else if(c > target) {
j--;
} else {
i++;
}
}
return null;
}
/**
* 剑指 Offer 58 - I. 翻转单词顺序
* 输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。
* 为简单起见,标点符号和普通字母一样处理。例如输入字符串"I am a student. ",则输出"student. a am I"。
* 示例 1:
* 输入: "the sky is blue"
* 输出: "blue is sky the"
* @param s
* @return
* 思路1:
*
*/
public String reverseWords(String s) {
if(s == null || s.length() == 0) {
return s;
}
String[] temp = s.trim().split(" ");
StringBuilder builder = new StringBuilder();
for (int i = temp.length - 1; i >= 0 ; i--) {
String t = temp[i];
if(t.length() > 0) {
builder.append(temp[i]).append(" ");
}
}
return builder.toString().trim();
}
}
双指针解决数组问题
左右指针 快慢指针
/**
* @author August
* @version 1.0
* @description: 在处理数组和链表相关问题时,双指针技巧是经常用到的,
* 双指针技巧主要分为两类:左右指针和快慢指针。
* @date 2022/9/21 17:17
*/
public class Pointer2ArrayPractice {
/**
* 26 题「 删除有序数组中的重复项」,让你在有序数组去重
* @param nums
* @return
*/
public int removeDuplicates(int[] nums) {
if(nums == null || nums.length == 0) return 0;
int slow = 0, fast = 0;
while(fast < nums.length) {
if(nums[fast] != nums[slow]) {
//维护nums[0..slow]无重复
nums[slow + 1] = nums[fast];
slow++;
}
fast++;
}
// 数组长度为索引 + 1
return slow + 1;
}
/**
* 83 题「 删除排序链表中的重复元素」
* @param head
* @return
*/
public ListNode deleteDuplicates(ListNode head) {
if(head == null || head.next == null) return head;
ListNode slow = head, fast = head;
while(fast != null) {
if(fast.val != slow.val) {
// nums[slow] = nums[fast];
slow.next = fast;
// slow++;
slow = slow.next;
}
fast = fast.next;
}
// 断开与后面重复元素的连接
slow.next = null;
return head;
}
/**
* 移除元素,返回新数组的长度
* @param nums
* @param val
* @return
*/
public int removeElement(int[] nums, int val) {
int slow = 0, fast = 0;
while(fast < nums.length) {
if(nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
}
fast++;
}
return slow;
}
/**
* 给你输入一个数组 nums,请你原地修改,将数组中的所有值为 0 的元素移到数组末尾,函数签名如下:
* @param nums
*/
public void moveZeroes(int[] nums) {
// 去除 nums 中的所有 0,返回不含 0 的数组长度
int p = removeElement(nums, 0);
// 将 nums[p..] 的元素赋值为 0
for (; p < nums.length; p++) {
nums[p] = 0;
}
}
//二分查找
int binarySearch(int[] nums, int target) {
// 一左一右两个指针相向而行
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid - 1;
}
return -1;
}
/**
* 167 给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
*
* 以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
*
* 你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
* @param nums
* @param target
* @return
*/
int[] twoSum(int[] nums, int target) {
// 一左一右两个指针相向而行
int l = 0, r = nums.length - 1;
while(l < r) {
int total = nums[l] + nums[r];
if(total == target) {
return new int[]{l+1, r+1};
} else if(total > target) {
r--;
} else {
l++;
}
}
return new int[]{-1, -1};
}
/**
* 反转字符串
* @param s
*/
public void reverseString(char[] s) {
if(s == null || s.length <= 1) return;
int l = 0, r = s.length - 1;
while(l < r) {
char t = s[l];
s[l] = s[r];
s[r] = t;
l++;
r--;
}
}
boolean isPalindrome(String s) {
// 一左一右两个指针相向而行
int left = 0, right = s.length() - 1;
while (left < right) {
if (s.charAt(left) != s.charAt(right)) {
return false;
}
left++;
right--;
}
return true;
}
/**
* 第 5 题「 最长回文子串」
* @param s
* @return
*/
String longestPalindrome(String s) {
if(s == null || s.length() == 1) return s;
String res = "";
for (int i = 0; i< s.length(); i++) {
String res1 = palindrome(s, i, i);
String res2 = palindrome(s, i,i+1);
if(res1.length() > res.length()) res = res1;
if(res2.length() > res.length()) res = res2;
}
return res;
}
// 在 s 中寻找以 s[l] 和 s[r] 为中心的最长回文串
String palindrome(String s, int l, int r) {
while(l >= 0 && r < s.length()) {
if(s.charAt(l) == s.charAt(r)) {
l--;
r++;
} else {
break;
}
}
return s.substring(l+1, r);
}
}
递归反转链表
递归操作链表并不高效。和迭代解法相比,虽然时间复杂度都是 O(N),但是迭代解法的空间复杂度是 O(1),而递归解法需要堆栈,空间复杂度是
O(N)。所以递归操作链表可以作为对递归算法的练习或者拿去和小伙伴装逼,但是考虑效率的话还是使用迭代算法更好
/**
* @author August
* @version 1.0
* @description: 递归反转链表
* @date 2022/9/19 15:17
*/
public class ListNodeRecursionPractice {
/**
* 递归反转链表
* @param head
* @return
*/
public ListNode reverse(ListNode head) {
if(head == null || head.next == null) {
return head;
}
ListNode newHead = reverse(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode successor = null;
ListNode reverseN(ListNode head, int n) {
if(head == null || head.next == null) {
return head;
}
if(n == 1) {
//第n+1个节点
successor = head.next;
return head;
}
//以 head.next 为起点,需要反转前 n - 1 个节点
ListNode newHead = reverseN(head.next, n - 1);
head.next.next = head;
head.next = successor;
return newHead;
}
/**
* 92 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。
* 请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
* @param head
* @param left
* @param right
* @return
*/
public ListNode reverseBetween(ListNode head, int left, int right) {
//首先,如果 m == 1,就相当于反转链表开头的 n 个元素嘛,也就是我们刚才实现的功能
//如果 m != 1 怎么办?如果我们把 head 的索引视为 1,那么我们是想从第 m 个元素开始反转对吧;
// 如果把 head.next 的索引视为 1 呢?那么相对于 head.next,反转的区间应该是从第 m - 1 个元素开始的;
// 那么对于 head.next.next 呢…… 区别于迭代思想,这就是递归思想
if(left == 1) {
return reverseN(head, right);
}
head.next = reverseBetween(head.next, left - 1, right - 1);
return head;
}
// 反转以 a 为头结点的链表
public ListNode reverse2(ListNode a) {
ListNode pre = null, cur = a, next = a.next;
while(cur != null) {
next = cur.next;
//逐个节点反转
cur.next = pre;
//更新指针位置
pre = cur;
cur = next;
}
return pre;
}
/** 反转区间 [a, b) 的元素,注意是左闭右开 */
ListNode reverse2(ListNode a, ListNode b) {
ListNode pre = null, cur = a, next = a.next;
while(cur != b) {
next = cur.next;
//逐个节点反转
cur.next = pre;
//更新指针位置
pre = cur;
cur = next;
}
return pre;
}
//k个一组反转链表
ListNode reverseKGroup(ListNode head, int k) {
if(head == null) {
return null;
}
//先获取第一个反转区间,然后反转,剩余链表使用递归
ListNode a = head;
ListNode b = head;
for (int i = 0; i < k; i++) {
// 不足 k 个,不需要反转,base case
if (b == null) return head;
b = b.next;
}
ListNode newHead = reverse2(a, b);
ListNode node = reverseKGroup(b, k);
a.next = node;
return newHead;
}
/**
* 234 判断回文单链表
*/
//左侧指针
ListNode left;
public boolean isPalindrome(ListNode head) {
//思路1 使用双指针找到中间位置,递归翻转链表的一部分 【时间复杂度O(n),空间复杂度O(1)】
//思路2【本例】 借助二叉树后序遍历的思路,不需要显式反转原始链表也可以倒序遍历链表 【时间复杂度O(n),空间复杂度O(n)】
left = head;
return traverse(head);
}
boolean traverse(ListNode right) {
if(right == null) return true;
boolean res = traverse(right.next);
//后序遍历
res = res && (right.val == left.val);
left = left.next;
return res;
}
public boolean isPalindrome2(ListNode head) {
ListNode slow = head , fast = head;
while(fast != null && fast.next != null) {
slow = head.next;
fast = fast.next.next;
}
if(fast != null) {
//奇数
slow = slow.next;
}
ListNode left = head;
ListNode right = reverse(slow);
while(right != null) {
if(left.val != right.val) {
return false;
}
left = left.next;
right = right.next;
}
return true;
}
}
tanxin
前缀数组
前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和。
提前计算 preSum[0…n],需要查询区间和时使用preSum相减,时间复杂度O(1)
差分数组
差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
维护一个差分数组,即每个元素相对于前一个元素的增量,对区间内元素增减时间复杂度O(1),需要查询元素的值时,根据差分数组计算
/**
* @author August
* @version 1.0
* @description: 差分数组工具类
* @date 2022/9/26 9:58
*/
public class Difference {
// 差分数组
private int[] diff;
/* 输入一个初始数组,区间操作将在这个数组上进行 */
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
/* 返回结果数组 */
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
/**
* 370 题「 区间加法」
* @param length
* @param updates
* @return
*/
int[] getModifiedArray(int length, int[][] updates) {
// nums 初始化为全 0
int[] nums = new int[length];
// 构造差分解法
Difference df = new Difference(nums);
for (int[] update : updates) {
int i = update[0];
int j = update[1];
int val = update[2];
df.increment(i, j, val);
}
return df.result();
}
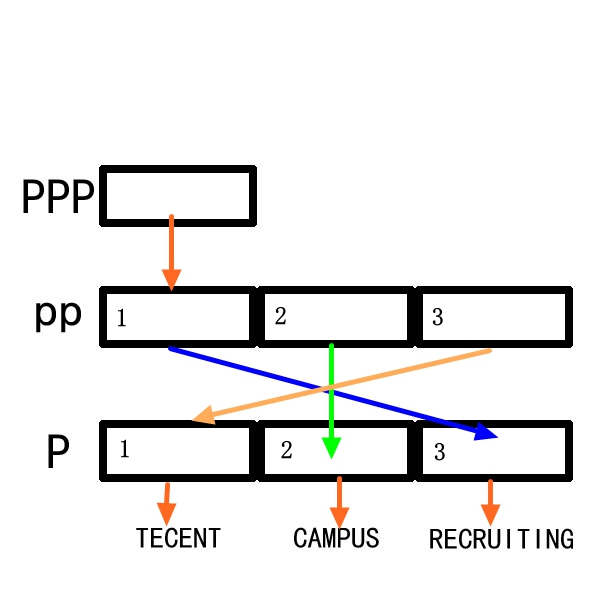
/**
* 1109. 航班预订统计
* 这里有 n 个航班,它们分别从 1 到 n 进行编号。
*
* 有一份航班预订表 bookings ,
* 表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意
* 味着在从 firsti 到 lasti (包含 firsti 和 lasti )的 每个航班 上预订了 seatsi 个座位。
*
* 请你返回一个长度为 n 的数组 answer,里面的元素是每个航班预定的座位总数。
* @param bookings
* @param n
* @return
*/
public int[] corpFlightBookings(int[][] bookings, int n) {
//n个航班,预定座位总数
int[] num = new int[n];
// 构造差分解法
Difference difference = new Difference(num);
for (int i = 0; i < bookings.length; i++) {
// 注意转成数组索引要减一哦
int firsti = bookings[i][0] - 1;
int lasti = bookings[i][1] - 1;
int seatsi = bookings[i][2];
difference.increment(firsti, lasti, seatsi);
}
// 返回最终的结果数组
return difference.result();
}
/**
* 第 1094 题「 拼车」
* 你是一个开公交车的司机,公交车的最大载客量为 capacity,
* 沿途要经过若干车站,给你一份乘客行程表 int[][] trips,
* 其中 trips[i] = [num, start, end] 代表着有 num 个旅客要从站点 start 上车,到站点 end 下车,
* 请你计算是否能够一次把所有旅客运送完毕(不能超过最大载客量 capacity)。
* @param trips
* @param capacity
* @return
*/
public boolean carPooling(int[][] trips, int capacity) {
//车辆到达车站后,车上乘客数量, 设定最多1001个车站
int[] nums = new int[1001];
// 构造差分解法
Difference difference = new Difference(nums);
for (int i = 0; i < trips.length; i++) {
// 注意转成数组索引要减一哦
int val = trips[i][0] ;
// 第 trip[1] 站乘客上车
int start = trips[i][1];
// 第 trip[2] 站乘客已经下车,
// 即乘客在车上的区间是 [trip[1], trip[2] - 1]
int end = trips[i][2] - 1;
difference.increment(start, end, val);
}
int[] res = difference.result();
for (int i = 0; i < res.length; i++) {
if(res[i] > capacity) {
return false;
}
}
return true;
}
滑动窗口(双指针、Rabin-Karp滑动哈希)
滑动窗口常用来解决子串问题。
滑动哈希:将字符串转为数字(hash运算,%较大的素数),提高效率,避免频繁的subString
package practice.array;
import java.util.*;
/**
* @author August
* @version 1.0
* @description: 滑动窗口(双指针)
* @date 2022/9/29 16:03
*/
public class SlideWindowPractice {
/**
* 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。
* 如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
* 注意:
*
* 对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
* 如果 s 中存在这样的子串,我们保证它是唯一的答案。
*
* 来源:力扣(LeetCode)
* 链接:https://leetcode.cn/problems/minimum-window-substring
* 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
* @param s
* @param t
* @return
*
* unordered_map 就是哈希表(字典),相当于 Java 的 HashMap,它的一个方法 count(key) 相当于 Java 的 containsKey(key)
* 可以判断键 key 是否存在。
*
* 可以使用方括号访问键对应的值 map[key]。
* 需要注意的是,如果该 key 不存在,C++ 会自动创建这个 key,并把 map[key] 赋值为 0。
* 所以代码中多次出现的 map[key]++ 相当于 Java 的 map.put(key, map.getOrDefault(key, 0) + 1)。
*
*/
public String minWindow(String s, String t) {
//t 中字符出现次数
Map<Character, Integer> need = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
char c = t.charAt(i);
need.put(c, need.getOrDefault(c, 0) + 1);
}
//窗口中字符出现次数
Map<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
//满足条件的字符数量
int valid = 0;
// 记录最小覆盖子串的起始索引及长度
int start = 0, len = Integer.MAX_VALUE;
while(right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
if(need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if(window.get(c).equals(need.get(c))) {
valid++;
}
}
//判断左侧窗口是否要收缩
while(valid == need.size()) {
// 在这里更新最小覆盖子串
if(right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if(need.containsKey(d)) {
if(window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.getOrDefault(d, 0) - 1);
}
}
}
return len == Integer.MAX_VALUE ? "": s.substring(start, start + len);
}
/**
* 567. 字符串的排列
* 给你两个字符串 s1 和 s2 ,
* 写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。
* 换句话说,s1 的排列之一是 s2 的 子串 。
* @param s1
* @param s2
* @return
*/
public boolean checkInclusion(String s1, String s2) {
//t 中字符出现次数
Map<Character, Integer> need = new HashMap<>();
for (int i = 0; i < s1.length(); i++) {
char c = s1.charAt(i);
need.put(c, need.getOrDefault(c, 0) + 1);
}
//窗口中字符出现次数
Map<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
//满足条件的字符数量
int valid = 0;
while(right < s2.length()) {
// c 是将移入窗口的字符
char c = s2.charAt(right);
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
if(need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if(window.get(c).equals(need.get(c))) {
valid++;
}
}
//判断左侧窗口是否要收缩
while(right - left >= s1.length()) {//因为定长窗口每次向前滑动时只会移出一个字符,所以可以把内层的 while 改成 if,效果是一样的
if(valid == need.size()) {
return true;
}
// d 是将移出窗口的字符
char d = s2.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if(need.containsKey(d)) {
if(window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.getOrDefault(d, 0) - 1);
}
}
}
return false;
}
/**
* 438. 找到字符串中所有字母异位词
* 给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,
* 返回这些子串的起始索引。不考虑答案输出的顺序。
*
* 异位词 指由相同字母重排列形成的字符串(包括相同的字符串)
* 输入: s = "cbaebabacd", p = "abc"
* 输出: [0,6]
* 解释:
* 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
* 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
*
* 来源:力扣(LeetCode)
* 链接:https://leetcode.cn/problems/find-all-anagrams-in-a-string
* 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
* 1 <= s.length, p.length <= 3 * 104
* s 和 p 仅包含小写字母
* @param t [p]
* @param s [s]
* @return
*/
public List<Integer> findAnagrams(String s, String t) {
//t 中字符出现次数
Map<Character, Integer> need = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
char c = t.charAt(i);
need.put(c, need.getOrDefault(c, 0) + 1);
}
//窗口中字符出现次数
Map<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
//满足条件的字符数量
int valid = 0;
// 记录返回结果
List<Integer> list = new ArrayList<>();
while(right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
if(need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if(window.get(c).equals(need.get(c))) {
valid++;
}
}
//判断左侧窗口是否要收缩
while(right - left >= t.length()) {
if(valid == need.size()) {
list.add(left);
}
// d 是将移出窗口的字符
char d = s.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if(need.containsKey(d)) {
if(window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.getOrDefault(d, 0) - 1);
}
}
}
return list;
}
/**
* 3. 无重复字符的最长子串
* 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
* @param s
* @return
*/
public int lengthOfLongestSubstring(String s) {
//t 中字符出现次数
Map<Character, Integer> need = new HashMap<>();
//窗口中字符出现次数
Map<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
// 记录返回结果
Integer res = 0;
while(right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
window.put(c, window.getOrDefault(c, 0) + 1);
//判断左侧窗口是否要收缩
while(window.getOrDefault(c, 0) > 1) {
//在这里更新答案。走到这一步就说明:遇到了第一个与当前窗口重复的字符,
if(right - left - 1 > res) {
res = right - left - 1;
}
// d 是将移出窗口的字符
char d = s.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
window.put(d, window.getOrDefault(d, 0) - 1);
}
//在这里更新答案。走到这一步就说明:遇到了第一个与当前窗口重复的字符 或者 当前无重复字符,
if(right - left > res) {
res = right - left;
}
}
return res;
}
/**
* 187. 重复的DNA序列
* DNA序列 由一系列核苷酸组成,缩写为 'A', 'C', 'G' 和 'T'.。
*
* 例如,"ACGAATTCCG" 是一个 DNA序列 。
* 在研究 DNA 时,识别 DNA 中的重复序列非常有用。
*
* 给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。
* 你可以按 任意顺序 返回答案。
* @param s
* @return
*/
public List<String> findRepeatedDnaSequences(String s) {
//窗口中字符出现次数
Map<String, Integer> window = new HashMap<>();
int left = 0, right = 10;
// 记录返回结果
List<String> result = new ArrayList<>();
while(right <= s.length()) {
//在这里更新答案。走到这一步就说明:遇到了第一个与当前窗口重复的字符,
String str = s.substring(left, right);
Integer curCount = window.getOrDefault(str, 0);
if(curCount == 1) {
result.add(str);
}
window.put(str, curCount + 1);
// 扩大窗口
right++;
// 缩小窗口
left++;
}
return result;
}
//滑动窗口算法本身的时间复杂度是 O(N),再看看窗口滑动的过程中的操作耗时,
// 给 res 添加子串的过程用到了 substring 方法需要 O(L) 的复杂度,但一般情况下 substring 方法不会调用很多次,
// 只有极端情况(比如字符串全都是相同的字符)下才会每次滑动窗口时都调用 substring 方法。
//
//所以我们可以说这个算法一般情况下的平均时间复杂度是 O(N),极端情况下的时间复杂度会退化成 O(NL)。
List<String> findRepeatedDnaSequences2(String s) {
// 先把字符串转化成四进制的数字数组
int[] nums = new int[s.length()];
for (int i = 0; i < nums.length; i++) {
switch (s.charAt(i)) {
case 'A':
nums[i] = 0;
break;
case 'G':
nums[i] = 1;
break;
case 'C':
nums[i] = 2;
break;
case 'T':
nums[i] = 3;
break;
}
}
// 记录重复出现的哈希值
HashSet<Integer> seen = new HashSet<>();
// 记录重复出现的字符串结果
HashSet<String> res = new HashSet<>();
// 数字位数
int L = 10;
// 进制
int R = 4;
// 存储 R^(L - 1) 的结果
int RL = (int) Math.pow(R, L - 1);
// 维护滑动窗口中字符串的哈希值
int windowHash = 0;
// 滑动窗口代码框架,时间 O(N)
int left = 0, right = 0;
while (right < nums.length) {
// 扩大窗口,移入字符,并维护窗口哈希值(在最低位添加数字)
windowHash = R * windowHash + nums[right];
right++;
// 当子串的长度达到要求
if (right - left == L) {
// 根据哈希值判断是否曾经出现过相同的子串
if (seen.contains(windowHash)) {
// 当前窗口中的子串是重复出现的
res.add(s.substring(left, right));
} else {
// 当前窗口中的子串之前没有出现过,记下来
seen.add(windowHash);
}
// 缩小窗口,移出字符,并维护窗口哈希值(删除最高位数字)
windowHash = windowHash - nums[left] * RL;
left++;
}
}
// 转化成题目要求的 List 类型
return new LinkedList<>(res);
}
/**
* Rabin-Karp 指纹字符串查找算法
*
* 滑动哈希避免截取字符串,从而提高效率
* X % Q == (X + Q) % Q
* (X + Y) % Q == (X % Q + Y % Q) % Q
* @param txt
* @param pat
* @return
*/
int rabinKarp(String txt, String pat) {
// 位数
int L = pat.length();
// 进制(只考虑 ASCII 编码)
int R = 256;
// 取一个比较大的素数作为求模的除数
long Q = 1658598167;
// R^(L - 1) 的结果
long RL = 1;
for (int i = 1; i <= L - 1; i++) {
// 计算过程中不断求模,避免溢出
RL = (RL * R) % Q;
}
// 计算模式串的哈希值,时间 O(L)
long patHash = 0;
for (int i = 0; i < pat.length(); i++) {
patHash = (R * patHash + pat.charAt(i)) % Q;
}
// 滑动窗口中子字符串的哈希值
long windowHash = 0;
// 滑动窗口代码框架,时间 O(N)
int left = 0, right = 0;
while (right < txt.length()) {
// 扩大窗口,移入字符
windowHash = ((R * windowHash) % Q + txt.charAt(right)) % Q;
right++;
// 当子串的长度达到要求
if (right - left == L) {
// 根据哈希值判断是否匹配模式串
if (windowHash == patHash) {
// 当前窗口中的子串哈希值等于模式串的哈希值
// 还需进一步确认窗口子串是否真的和模式串相同,避免哈希冲突
if (pat.equals(txt.substring(left, right))) {
return left;
}
}
// 缩小窗口,移出字符
windowHash = (windowHash - (txt.charAt(left) * RL) % Q + Q) % Q;
// X % Q == (X + Q) % Q 是一个模运算法则
// 因为 windowHash - (txt[left] * RL) % Q 可能是负数
// 所以额外再加一个 Q,保证 windowHash 不会是负数
left++;
}
}
// 没有找到模式串
return -1;
}
}
二叉树
二叉树题目的递归解法可以分两类思路,第一类是遍历一遍二叉树得出答案,第二类是通过分解问题计算出答案,这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架。
排序算法
归并排序
分解子问题,对左区间和右区间分别排序,然后合并【合并两个有序数组】,使用递归的思维,相当于后序遍历
快速排序
选择一个数组第一个节点,进行排序【比节点小的放左边,其他放右边】,再对左右区间重复排序操作,相当于前序遍历
1 数据结构
二叉堆
二叉堆
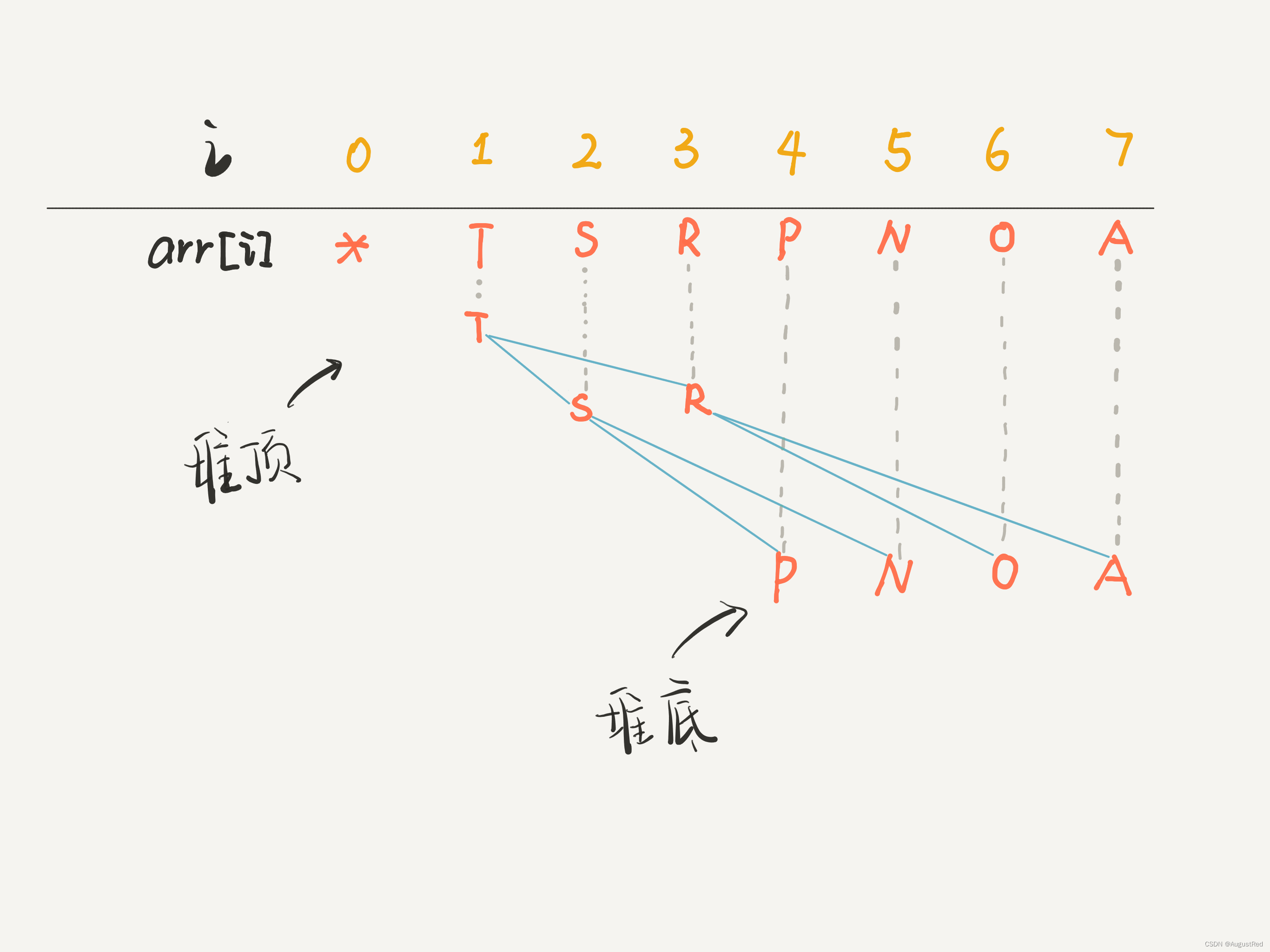
二叉堆就是一种完全二叉树,所以适合存储在数组中,而且二叉堆拥有一些特殊性质。
二叉堆的操作很简单,主要就是上浮和下沉,来维护堆的性质(堆有序),核心代码也就十行。
优先级队列是基于二叉堆实现的,主要操作是插入和删除。插入是先插到最后,然后上浮到正确位置;删除是调换位置后再删除,然后下沉到正确位置。核心代码也就十行。
图
本质上图可以认为是多叉树的延伸
一幅图是由节点和边构成的,逻辑结构如下:
/* 图节点的逻辑结构 */
class Vertex {
int id;
Vertex[] neighbors;
}
一般用常说的邻接表和邻接矩阵来实现。
// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;
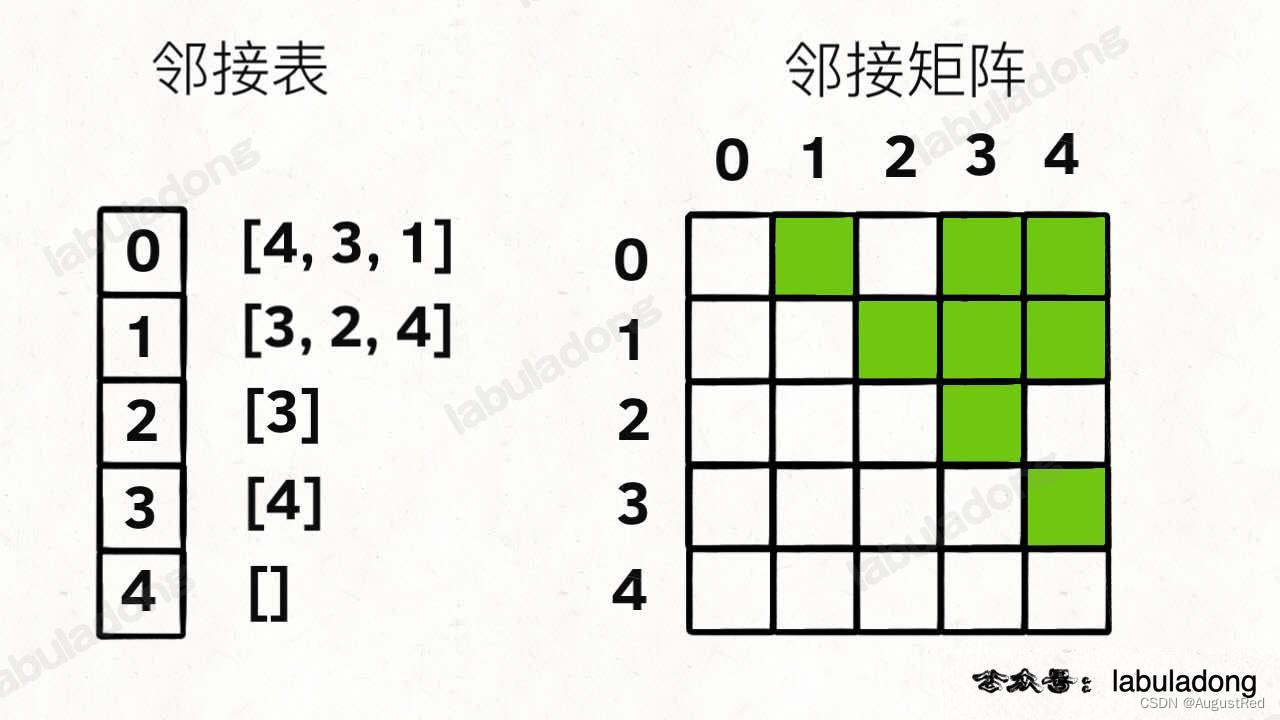
那么,为什么有这两种存储图的方式呢?肯定是因为他们各有优劣。
对于邻接表,好处是占用的空间少。
你看邻接矩阵里面空着那么多位置,肯定需要更多的存储空间。
但是,邻接表无法快速判断两个节点是否相邻。
比如说我想判断节点 1 是否和节点 3 相邻,我要去邻接表里 1 对应的邻居列表里查找 3 是否存在。但对于邻接矩阵就简单了,只要看看 matrix[1][3] 就知道了,效率高。
所以说,使用哪一种方式实现图,要看具体情况。
PS:在常规的算法题中,邻接表的使用会更频繁一些,主要是因为操作起来较为简单,但这不意味着邻接矩阵应该被轻视。矩阵是一个强有力的数学工具,图的一些隐晦性质可以借助精妙的矩阵运算展现出来。不过本文不准备引入数学内容,所以有兴趣的读者可以自行搜索学习。
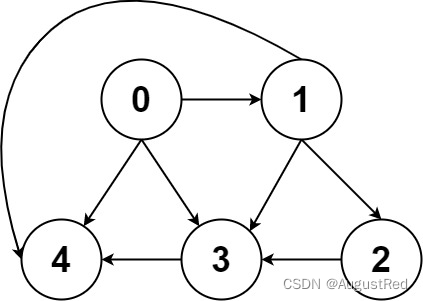
最后,我们再明确一个图论中特有的度(degree)的概念,在无向图中,「度」就是每个节点相连的边的条数。
由于有向图的边有方向,所以有向图中每个节点「度」被细分为入度(indegree)和出度(outdegree),比如下图:
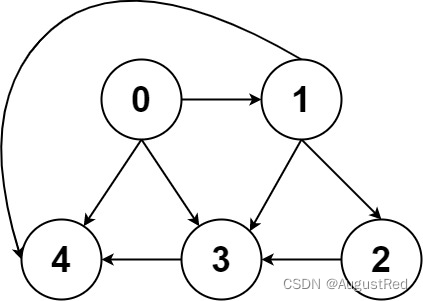
好了,对于「图」这种数据结构,能看懂上面这些就绰绰够用了。
那你可能会问,我们上面说的这个图的模型仅仅是「有向无权图」,不是还有什么加权图,无向图,等等……
其实,这些更复杂的模型都是基于这个最简单的图衍生出来的。
有向加权图怎么实现?很简单呀:
如果是邻接表,我们不仅仅存储某个节点 x 的所有邻居节点,还存储 x 到每个邻居的权重,不就实现加权有向图了吗?
如果是邻接矩阵,matrix[x][y] 不再是布尔值,而是一个 int 值,0 表示没有连接,其他值表示权重,不就变成加权有向图了吗?
如果用代码的形式来表现,大概长这样:
// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
List<int[]>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重,0 表示不相邻
int[][] matrix;
无向图怎么实现?也很简单,所谓的「无向」,是不是等同于「双向」?
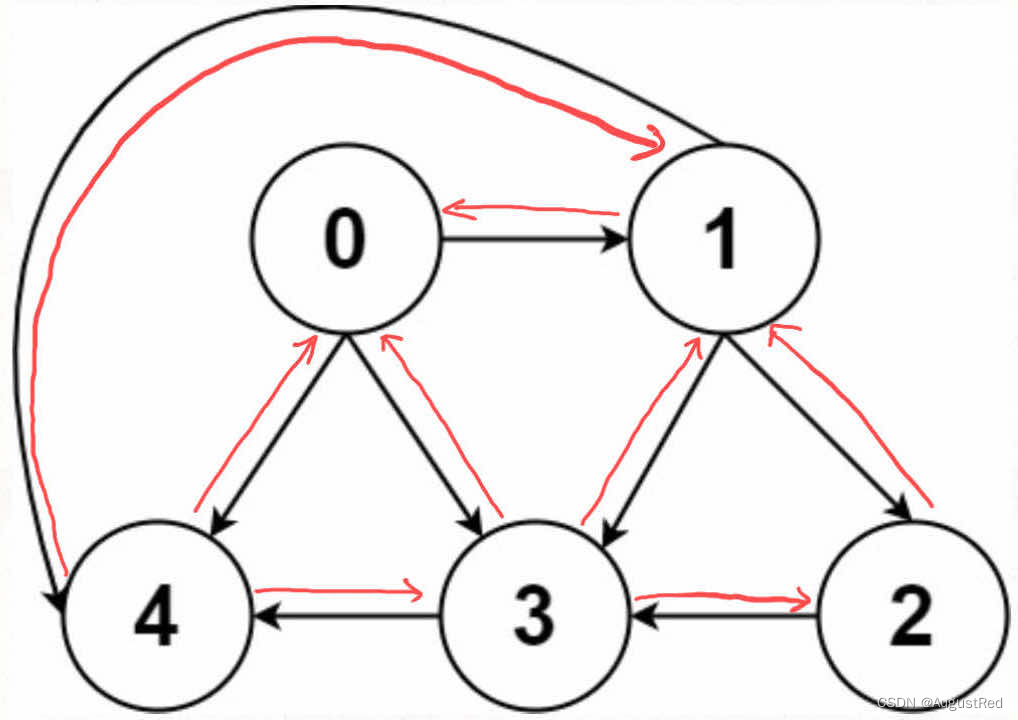
遍历
图和多叉树最大的区别是,图是可能包含环的,你从图的某一个节点开始遍历,有可能走了一圈又回到这个节点,而树不会出现这种情况,从某个节点出发必然走到叶子节点,绝不可能回到它自身。
所以,如果图包含环,遍历框架就要一个 visited 数组进行辅助:
// 记录被遍历过的节点;visited 数组就是防止递归重复遍历同一个节点进入死循环的。
boolean[] visited;
// 记录从起点到当前节点的路径;nPath 数组的操作很像前文 回溯算法核心套路 中做「做选择」和「撤销选择」,区别在于位置:回溯算法的「做选择」和「撤销选择」在 for 循环里面,而对 onPath 数组的操作在 for 循环外面
boolean[] onPath;
/* 图遍历框架 */
void traverse(Graph graph, int s) {
if (visited[s]) return;
// 经过节点 s,标记为已遍历
visited[s] = true;
// 做选择:标记节点 s 在路径上
onPath[s] = true;
for (int neighbor : graph.neighbors(s)) {
traverse(graph, neighbor);
}
// 撤销选择:节点 s 离开路径
onPath[s] = false;
}
拓扑排序
拓扑排序(Topological Sorting)
直观地说就是,让你把一幅图「拉平」,而且这个「拉平」的图里面,所有箭头方向都是一致的,比如上图所有箭头都是朝右的。
很显然,如果一幅有向图中存在环,是无法进行拓扑排序的,因为肯定做不到所有箭头方向一致;反过来,如果一幅图是「有向无环图」,那么一定可以进行拓扑排序。
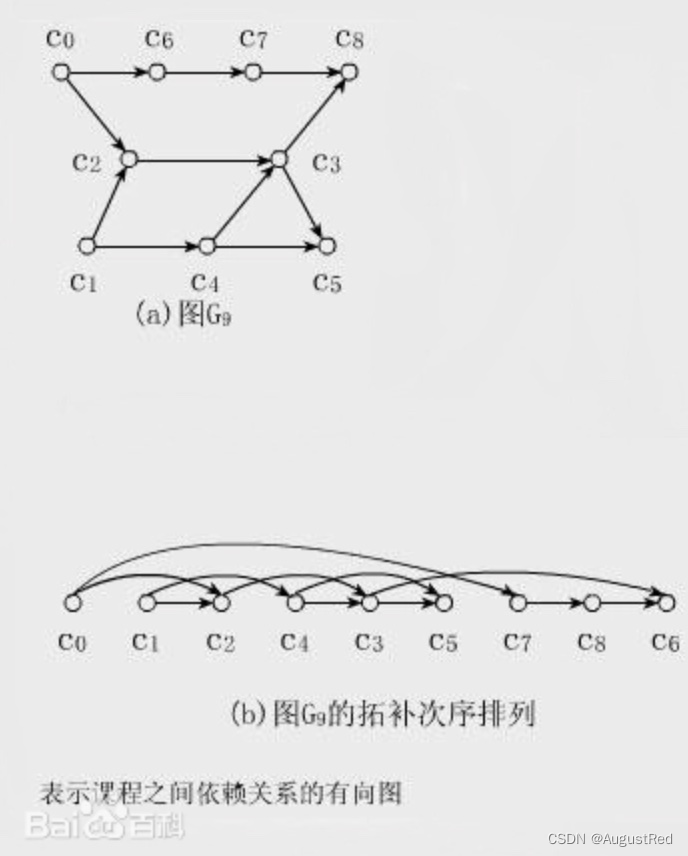
PS:图片中拓扑排序的结果有误,C7->C8->C6 应该改为 C6->C7->C8





![SSM整合案例[企业权限管理系统]-学习笔记01【SVN的基本介绍】](https://img-blog.csdnimg.cn/5eaf7bb30a474bac9da267b9986d3ba6.png)