倍增算法
文章目录
- 倍增算法
- 定义
- 倍增在序列上的应用
- 查找
- 例一
- 例二
- 快速幂
- RMQ(区间最值)
- 天才的记忆
- LCA(最近公共祖先)
- 向上标记法
- 树上倍增法
- 祖孙询问
- Tarjan算法
- 距离
- 总结
定义
倍增 从字面的上意思看就是成倍的增长 ,这是指我们在进行递推时,如果状态空间很大,通常的线性递推无法满足时间和空间复杂度的要求 ,那么我们就可以通过成倍的增长,只递推状态空间中在 2 的整数次幂位置上的值作为代表 。
倍增在序列上的应用
一般分为两个阶段,如图。
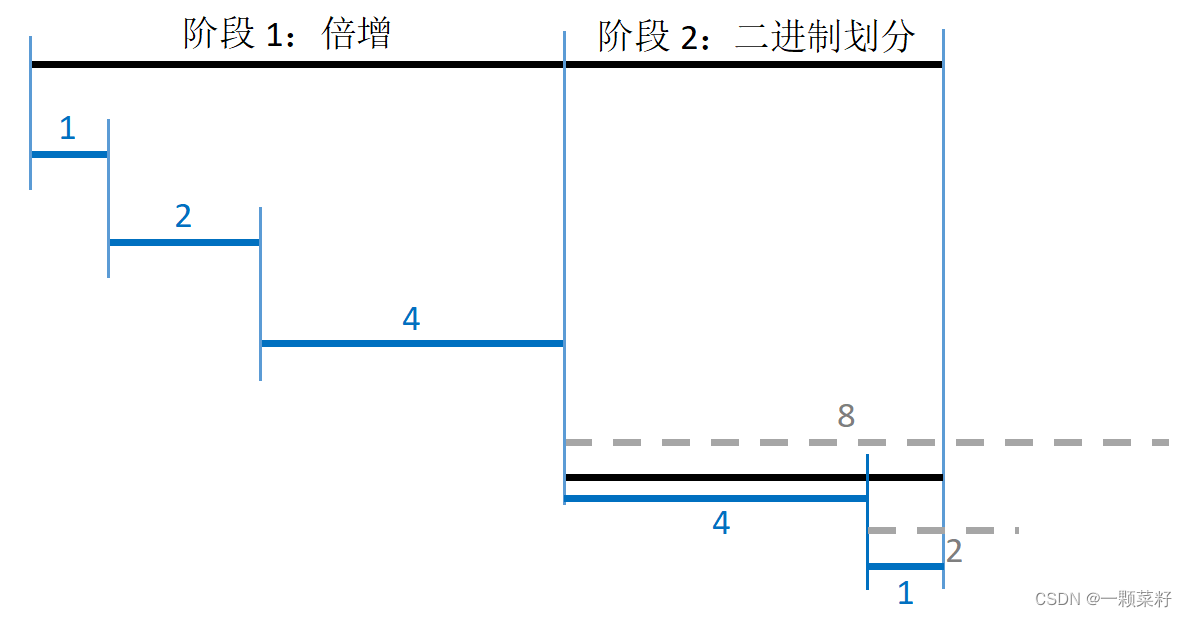
阶段1:倍增找到一个满足条件的边界
阶段2:将边界与目标的距离进行二进制划分。
查找
例一
在一个元素递增数组a中查找最大的小于一个数b的数字。
倍增做法:设定一个增长长度p和指示当前所指数字的指针k。先尝试a[k + p]是否满足小于b的条件,若满足条件,则p成2倍增长;否则p缩小范围,继续尝试,直到p缩小到0为止。
def binary_lift(a, b) :
k, p = 0, 1
while p : #如果还能扩展k范围则继续扩展
if k + p - 1 <= len(a) and a[k + p - 1] < b :
k += p # 扩展范围
p <<= 1 #倍增
else :
p >>= 1 # 二进制划分
print(k)
例二
给定长度为 N N N的数列 A A A,然后在线询问若干次,每次给定一个整数 T T T,求出最大的 k k k,满足 ∑ i = 1 k A [ i ] ≤ T \sum^k_{i=1}A[i]\le T ∑i=1kA[i]≤T。
def binary_lift(a, t) :
length = len(a)
S = [0] * (length + 1)
for i in range(1, length + 1) : #前缀和
S[i] += S[i - 1] + a[i]
k, p, sum = 0, 1, 0
while p :
if k + p <= length and sum + S[k + p] - S[k] <= t : # 倍增
sum += S[k + p] - S[k]
k += p
k >>= 1 # 扩大范围
else : p <<= 1 #二进制划分
快速幂
求 a 的 b 次方对 p 取模的值。
输入格式
三个整数 a,b,p ,在同一行用空格隔开。
输出格式
输出一个整数,表示
a
b
m
o
d
p
a^b mod p
abmodp的值。
数据范围
0≤a,b≤109
1≤p≤109
输入样例:
3 2 7
输出样例:
2
def q_mi(a, b, p) :
res = 1
while b :
if b & 1 :
res = res * a % p
b >>= 1 #二进制划分
a = a * a % p # 倍增
return res % p
a, b, p = map(int, input().split())
print(q_mi(a, b, p))
RMQ(区间最值)
RMQ 是 R a n g e M a x i m u m / M i n i m u m Q u e r y Range Maximum/Minimum Query RangeMaximum/MinimumQuery的缩写,表示区间最大(最小)值。使用倍增思想解决 RMQ 问题的方法是 ST 表。
- 预处理部分
一个序列的子区间个数显然有 O ( N 2 ) O(N^2) O(N2)个,根据倍增思想,我们首先在这个规模为 O ( N 2 ) O(N^2) O(N2)的状态空间中选择一些2的整数次幂的位置作为代表值。
设f[i, j]表示从i开始长度是 2 j 2^j 2j的区间的最大值。递推边界为f[i, 0] = a[i], 公式 f [ i , j ] = m a x ( f [ i , j − 1 ] , f [ i + 2 j − 1 , j − 1 ] ) f[i, j]= max(f[i, j - 1], f[i + 2^{j - 1}, j - 1]) f[i,j]=max(f[i,j−1],f[i+2j−1,j−1]),即长度为 2 j 2^j 2j的子区间的最大值是左右两半长度最大值中较大的一个。 - 询问部分
当询问任意区间 [ l , r ] [l, r] [l,r]的最值时,我们先计算一个k,使得从l开始的 2 k 2^k 2k个数和以r结尾的 2 k 2^k 2k个数这两段一定覆盖了整个区间[l, r]。这样就能求出最值 m a x ( f [ l , k ] , f [ r − 2 k + 1 , k ) max(f[l, k], f[r - 2^k + 1, k) max(f[l,k],f[r−2k+1,k)。则 2 k < r − l + 1 ≤ 2 ∗ 2 k 2^k <r - l + 1\le 2 * 2^ k 2k<r−l+1≤2∗2k。所以 k = l o g 2 ( r − l + 1 ) k = log_2(r - l + 1) k=log2(r−l+1)
天才的记忆
从前有个人名叫 WNB,他有着天才般的记忆力,他珍藏了许多许多的宝藏。
在他离世之后留给后人一个难题(专门考验记忆力的啊!),如果谁能轻松回答出这个问题,便可以继承他的宝藏。
题目是这样的:给你一大串数字(编号为 1 到 N,大小可不一定哦!),在你看过一遍之后,它便消失在你面前,随后问题就出现了,给你 M 个询问,每次询问就给你两个数字 A,B,要求你瞬间就说出属于 A 到 B 这段区间内的最大数。
一天,一位美丽的姐姐从天上飞过,看到这个问题,感到很有意思(主要是据说那个宝藏里面藏着一种美容水,喝了可以让这美丽的姐姐更加迷人),于是她就竭尽全力想解决这个问题。
但是,她每次都以失败告终,因为这数字的个数是在太多了!
于是她请天才的你帮他解决。如果你帮她解决了这个问题,可是会得到很多甜头的哦!
输入格式
第一行一个整数 N 表示数字的个数。
接下来一行为 N 个数,表示数字序列。
第三行读入一个 M,表示你看完那串数后需要被提问的次数。
接下来 M 行,每行都有两个整数 A,B。
输出格式
输出共 M 行,每行输出一个数,表示对一个问题的回答。
数据范围
1≤N≤2×105,
1≤M≤104,
1≤A≤B≤N。
输入样例:
6
34 1 8 123 3 2
4
1 2
1 5
3 4
2 3
输出样例:
34
123
123
8
from math import log
N, M = 200010, 18
f = [[0] * M for _ in range(N)]
a = [0] * N
# 预处理部分
def init() :
for i in range(1, n + 1) :
f[i][0] = a[i]
k = int(log(n, 2)) + 1
for length in range(1, k) :
for l in range(1, n + 1) :
r = l + (1 << length) - 1
if r > n : break
f[l][length] = max(f[l][length - 1], f[l + (1 << (length - 1))][length - 1]) # 倍增
#查询部分
def query(l, r) :
k = int(log(r - l + 1, 2))
return max(f[l][k], f[r - (1 << k) + 1][k])
n = int(input())
a[1 : n + 1] = list(map(int, input().split()))
init()
m = int(input())
for i in range(m) :
l, r = map(int, input().split())
print(query(l, r))
LCA(最近公共祖先)
最近公共祖先简称 LCA(Lowest Common Ancestor)。两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。 为了方便,我们记某点集 S = { v 1 , v 2 , … , v n } S=\{v_1,v_2,\ldots,v_n\} S={v1,v2,…,vn} 的最近公共祖先为 LCA ( v 1 , v 2 , … , v n ) \text{LCA}(v_1,v_2,\ldots,v_n) LCA(v1,v2,…,vn)或 LCA ( S ) \text{LCA}(S) LCA(S)。
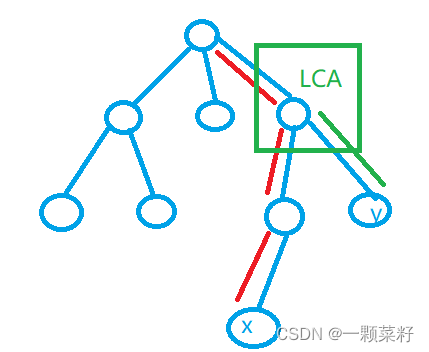
向上标记法
O ( n m ) O(nm) O(nm)
从x向上走到根节点,并标记所有经过的节点。
从y向上走到根节点,当第一次遇到已标记的节点时,就找到LCA(x, y)。
st = [False] * N
ans = 0
def sign(root, x) :
if root == x : # 访问节点为x返回True
st[root] = True
return True
i = h[root]
while ~ i :
j = e[i]
if sign(j, x) : # 标记路径上含有x的情况
st[j] = True
return True
i = ne[i]
return False
falg = True
def dfs(root, y) :
global ans
if root == y :
return True
i = h[root]
while ~ i :
j = e[i]
if dfs(j) :
if st[j] and flag:
ans = j
flag = False #标记第一次遇见已标记点状态
return True
i = ne[i]
return False
def lca(x, y) :
sign(root, x)
dfs(root, y)
return ans
树上倍增法
在线求LCA O ( n l o g n ) O(nlogn) O(nlogn)
- 预处理部分
设f[x, k]表示 x x x的 2 k 2^k 2k辈祖先,即从x向根节点走 2 k 2^k 2k步到达的节点。特别的,若该节点不存在,则令f[x, k] = 0.f[x, 0]就是x的父节点。除此之外, ∀ k ∈ [ 1 , l o g n ] , f [ x , k ] = [ f [ x , k − 1 ] , k − 1 ] \forall k\in[1, logn], f[x, k] = [f[x, k - 1], k - 1] ∀k∈[1,logn],f[x,k]=[f[x,k−1],k−1] - 查询部分
基于f数组计算LCA(x, y)分为以下几步:- 设d[x]表示x的深度。不妨 d [ x ] ≥ d [ y ] d[x] \ge d[y] d[x]≥d[y](否则可以交换x, y)
- 用二进制拆分思想,把x向上调整到y同一深度。
- 若此时 x = = y x == y x==y,说明已经找到了LCA,LCA 就等于y
- 用二进制拆分思想,把x,y同时向上调整,并保持深度一致,且二者不会相会。
- 此时x,y必定只差一步就相会了,它们的父节点就是LCA了。
祖孙询问
给定一棵包含 n 个节点的有根无向树,节点编号互不相同,但不一定是 1∼n。
有 m 个询问,每个询问给出了一对节点的编号 x 和 y,询问 x 与 y 的祖孙关系。
输入格式
输入第一行包括一个整数 表示节点个数;
接下来 n 行每行一对整数 a 和 b,表示 a 和 b 之间有一条无向边。如果 b 是 −1,那么 a 就是树的根;
第 n+2 行是一个整数 m 表示询问个数;
接下来 m 行,每行两个不同的正整数 x 和 y,表示一个询问。
输出格式
对于每一个询问,若 x 是 y 的祖先则输出 1,若 y 是 x 的祖先则输出 2,否则输出 0。
数据范围
1≤n,m≤4×104,
1≤每个节点的编号≤4×104
输入样例:
10
234 -1
12 234
13 234
14 234
15 234
16 234
17 234
18 234
19 234
233 19
5
234 233
233 12
233 13
233 15
233 19
输出样例:
1
0
0
0
2
from math import log
from collections import deque
N, M = 40010, 18
h = [-1] * N
e = [0] * N * 2
ne = [-1] * N * 2
idx = 0
f = [[0] * M for _ in range(N)]
d = [0] * N
def add(a, b) :
global idx
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx += 1
def bfs(root) :
que = deque()
que.appendleft(root)
d[root] = 1
while len(que) :
t = que.pop()
i = h[t]
while ~ i :
j = e[i]
if not d[j] : #防止向上遍历
que.appendleft(j)
d[j] = d[t] + 1
f[j][0] = t
for k in range(1, length) : # 倍增
f[j][k] = f[f[j][k - 1]][k - 1]
i = ne[i]
def lca(a, b) :
if d[a] < d[b] : a, b = b, a
for i in range(length, -1, -1) : # 二进制拆分
if d[f[a][i]] >= d[b] : # 尝试跳跃i距离,最终必定跳到与b同一高度
a = f[a][i]
if a == b : return b
for i in range(length, -1, -1) : # 二进制拆分
if f[a][i] != f[b][i] : # 尝试跳跃,如果没跳跃到公共祖先节点,否则缩小区间再跳。
a, b = f[a][i], f[b][i]
return f[a][0]
n = int(input())
length = int(log(n, 2)) + 1
root = 0
for i in range(n) :
a, b = map(int, input().split())
if ~ b :
add(a, b), add(b, a)
else : root = a
bfs(root)
m = int(input())
for i in range(m) :
a, b = map(int, input().split())
p = lca(a, b)
if p == a : print(1)
elif p == b : print(2)
else : print(0)
Tarjan算法
离线求LCA O ( n + m ) O(n + m) O(n+m)
Tarjan算法本质是使用并查集对“向上标记法”的优化。
在深度优先遍历的任意时刻,树中节点分为3类:
- 已经访问完毕并且回溯的节点。在这些节点标记一个整数2.
- 已经开始递归,但尚未回溯的节点。这些节点就是当前正在访问的节点x以及x的祖先。在这些节点上标记一个整数1.
- 尚未访问的节点。这些节点没有标记。
对于正在访问的节点
x
x
x,它到根节点的路径已经标记为1.若y是已经访问完毕并且回溯的节点,则LCA(x, y)就是从y向上走到根,第一个遇到标记为1的节点。
可以利用并查集进行优化,当一个节点获得整数2的标记时,把它所在的集合合并到它父节点所在的集合中(合并时它的父节点的标记一定为1,且单独构成一个集合)。
这相当于每个完成回溯的节点都有一个指针指向它的父节点,只需要查询y所在集合代表元素,就等价于y一直向上一直走到一个开始递归但尚未回溯的节点(标记1),即LCA(x, y)
距离
给出 n 个点的一棵树,多次询问两点之间的最短距离。
注意:
边是无向的。
所有节点的编号是 1,2,…,n。
输入格式
第一行为两个整数 n 和 m。n 表示点数,m 表示询问次数;
下来 n−1 行,每行三个整数 x,y,k,表示点 x 和点 y 之间存在一条边长度为 k;
再接下来 m 行,每行两个整数 x,y,表示询问点 x 到点 y 的最短距离。
树中结点编号从 1 到 n。
输出格式
共 m 行,对于每次询问,输出一行询问结果。
数据范围
2≤n≤104,
1≤m≤2×104,
0<k≤100,
1≤x,y≤n
输入样例1:
2 2
1 2 100
1 2
2 1
输出样例1:
100
100
输入样例2:
3 2
1 2 10
3 1 15
1 2
3 2
输出样例2:
10
25
N = 10010
M = N * 2
h = [-1] * N
e = [0] * M
w = [0] * M
ne = [-1] * M
idx = 0
dist = [0] * N
res = [0] * M
st = [0] * N
p = [0] * N
query = [[] for _ in range(N)]
def add(a, b, c) :
global idx
e[idx] = b
w[idx] = c
ne[idx] = h[a]
h[a] = idx
idx += 1
def find(x) :
if x != p[x] : p[x] = find(p[x])
return p[x]
def dfs(u, fa) : #求每个节点到根节点距离
i = h[u]
while ~ i :
j = e[i]
if j != fa : #防止回父节点
dist[j] = dist[u] + w[i]
dfs(j, u)
i = ne[i]
def tarjan(u) :
st[u] = 1
i = h[u]
while ~ i :
j = e[i]
if not st[j] : # 防止多次遍历
tarjan(j)
p[j] = u # 回溯完合并到此时为1的节点的集合
i = ne[i]
for item in query[u] :
y, id = item[0], item[1]
anc = find(y)
if st[y] == 2 :
res[id] = dist[u] + dist[y] - dist[anc] * 2
st[u] = 2 #标记回溯
n, m = map(int, input().split())
for i in range(n - 1) :
a, b, c = map(int, input().split())
add(a, b, c), add(b, a, c)
for i in range(1, n + 1) : #初始化并查集
p[i] = i
for i in range(m) :
a, b = map(int, input().split())
if a != b :
query[a].append([b, i])
query[b].append([a, i])
dfs(1, -1)
tarjan(1)
for i in range(m) :
print(res[i])
总结
其实很多二进制优化的题目,都可以归结为倍增和二进制拆分,多重背包就是个例子。