文章目录
- 逻辑结构
- 物理结构
- 顺序栈
- 链栈
- 共享栈
- 数据的操作
- 顺序栈的基本操作
- 链栈的基本操作
- 共享栈的基本操作
- 数据结构的应用
- 栈在括号匹配中的应用
- 栈在表达式求值中的应用
- 栈在递归调用中的应用
逻辑结构
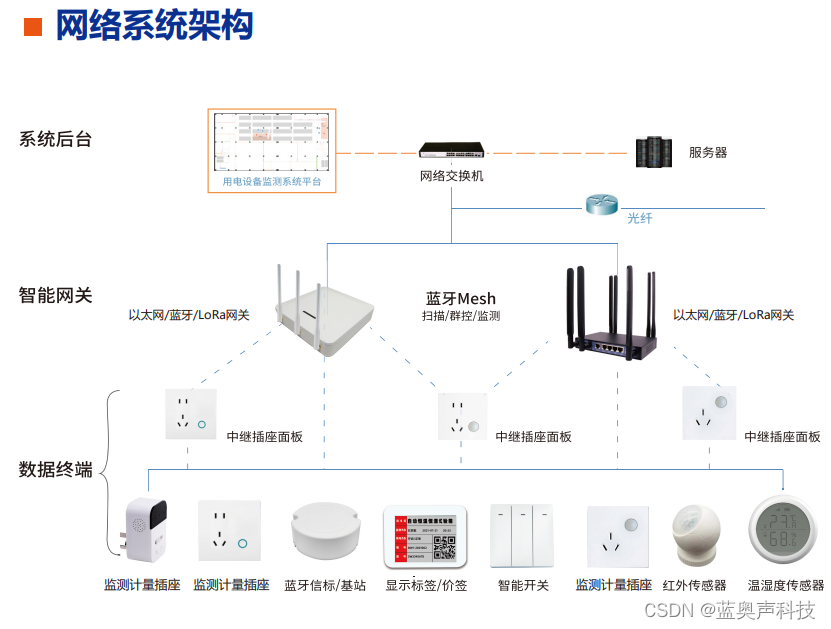
栈是只允许在一端进行插入或删除操作的线性表。首先栈是一种线性表,但限定这种线性表只能在某一端进行插入和删除操作。
栈的数学性质:当 n n n个不同的元素进栈时,出栈元素的不同排列个数为 1 n + 1 C 2 n n \frac{1}{n+1}C_{2n}^n n+11C2nn(卡特兰公式)。
物理结构
顺序栈
利用静态数组实现,并需要记录栈顶指针,且栈的大小不可改变。
typedef struct {
int data[Maxsize]; // 定义栈中元素
int top; // 定义栈顶指针
} SqStack;
链栈
利用链表实现,只需要记录头指针,利用链表的头插法实现进栈操作,解决了顺序栈中栈的大小不可扩充的问题。

typedef struct LinkNode {
int data; // 数据域
struct LinkNode *next; // 指针域
} LinkNode, *LiStack;
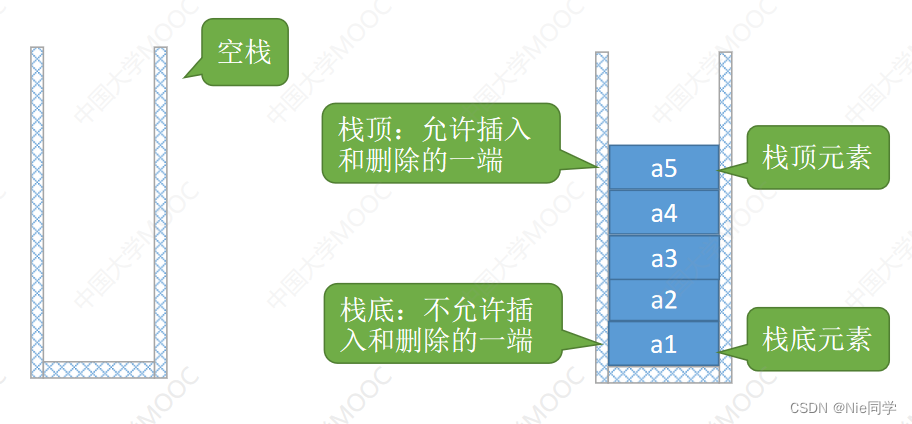
共享栈
利用栈底位置的相对不变性,可以让两个顺序栈共享一个一维数组,将两个栈的栈底分别设置在共享空间的两端,两个栈的栈顶向共享空间的中间延伸,解决了顺序栈空间利用率不足的问题。
typedef struct {
int data[Maxsize]; // 数据域
int top1, top 2; // 两个栈顶指针
} SStack;
数据的操作
顺序栈的基本操作
初始化
void InitStack(SqStack &s)
{
s.top = -1;
}
判断栈为空
bool isEmpty(SqStack s)
{
if (s.top == -1) return true;
return false;
}
判断栈为满
bool isFull(SqStack s)
{
if (s.top == Maxsize - 1) return true;
return false;
}
入栈
bool Push(SqStack &s, int x)
{
if (!isFull(s))
{
s.data[ ++ s.top] = x;
return true;
}
return false;
}
出栈
bool Pop(SqStack &s, int &x)
{
if (!isEmpty(s))
{
x = s.data[s.top -- ];
return true;
}
return false;
}
读取栈顶元素
bool GetTop(SqStack s, int &x)
{
if (!isEmpty(s))
{
x = s.data[s.top];
return true;
}
return false;
}
链栈的基本操作
初始化
void InitStack(LiStack s)
{
s->next = NULL;
}
判断栈为空
bool isEmpty(LiStack s)
{
if (s->next == NULL) return true;
return false;
}
入栈
bool Push(LiStack s, int x)
{
LinkNode *t = (LinkNode *) malloc (sizeof(LinkNode));
t->next = s->next;
s->next = t;
return true;
}
出栈
bool Pop(SqStack s, int &x)
{
if (!isEmpty(s))
{
LinkNode *t = s->next;
x = t->data;
s->next = t->next;
free(t);
return true;
}
return false;
}
读取栈顶元素
bool GetTop(SqStack s, int &x)
{
if (!isEmpty(s))
{
x = s->next->data;
return true;
}
return false;
}
共享栈的基本操作
初始化
void InitStack(SStack &s)
{
s.top1 = -1;
s.top2 = Maxsize;
}
判断栈为空(true:判断栈1,false:判断栈2)
bool isEmpty(SStack s, bool flag)
{
if (s.top1 == -1 && flag) return true;
else if (s.top2 == Maxsize && !flag) return true;
return false;
}
判断栈为满
bool isFull(SStack s)
{
if (s.top1 + 1 == s.top2) return true;
return false;
}
入栈(true:入栈1,false:入栈2)
bool Push(SStack &s, int x, bool flag)
{
if (!isFull(s))
{
if (flag) s.data[ ++ top1] = x;
else s.data[ -- top2] = x;
return true;
}
return false;
}
出栈(true:出栈1,false:出栈2)
bool Pop(SStack &s, int &x, bool flag)
{
if (!isEmpty(s, flag))
{
if (flag) x = s.data[top -- ];
else x = s.data[top ++ ];
return true;
}
return false;
}
读取栈顶元素(true:读栈1,false:读栈2)
bool GetTop(SStack s, int &x)
{
if (!isEmpty(s, flag))
{
if (flag) x = s.data[top];
else x = s.data[top];
return true;
}
return false;
}
数据结构的应用
栈在括号匹配中的应用

bool bracketCheck(char str[], int length)
{
SqStack s, InitStack(s);
for (int i = 0; i < length; i ++ )
{
if (str[i] == '(' || str[i] == '[' || str[i] == '{') // 遇到左括号进栈
Push(s, str[i]);
else
{
if (isEmpty(s)) return false; // 若遇到右括号,但栈是空的,证明左括号多了一个,则匹配不成功
char topElem;
Pop(s, topElem);
/*左右括号不匹配*/
if (str[i] == ')' && topElem != '(') return false;
if (str[i] == ']' && topElem != '[') return false;
if (str[i] == '}' && topElem != '{') return false;
}
}
return isEmpty(s); // 左右括号全部匹配
}
栈在表达式求值中的应用


- 栈中运算符的优先级高于当前运算符的优先级时:可以得出基于栈顶元素的运算就可以被确定了。
- 栈中运算符的优先级等于当前运算符的优先级时:基于左优先原则(左侧先做运算)。
其实就是中缀表达式转后缀表达式的过程中,边转换边计算(一旦确定运算就直接计算,再计算完的操作数压回栈中)就可以实现表达式的求值。
计算单元
void eval(Stack<int> &num, Stack<char> &op)
{
int x = num.top();
num.pop();
int y = num.top();
num.pop();
char c = op.top();
op.pop();
if (c == '+')
num.push(x + y);
else if (c == '-')
num.push(y - x);
else if (c == '*')
num.push(x * y);
else
num.push(y / x);
}
计算表达式单元
int exEval(char str[], int length)
{
unordered_map<char, int> pr = {{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}}; // 定义运算符的优先级
Stack<int> num;
Stack<char> op;
` for (int i = 0; i < length; i ++ )
{
if (isdigit(str[i]))
{
int x = 0;
while (i < length && isdigit(str[i])) x = x * 10 + (str[i] - '0'), i ++ ; // 将字符类型转换成数字
num.push(x);
i -- ;
}
else if (str[i] == '(') op.push(str[i]);
else if (str[i] == ')')
{
while (op.top() != '(') eval(num, op); // 将括号内的所有表达式已确定,直接计算
op.pop();
}
else // 操作符的情况
{
while (op.size() && op.top() != '(' && pr[op.top()] >= pr[str[i]]) eval(num, op); // 将已确定的运算式计算
op.push(str[i]); // 将待定运算符入栈
}
}
while (op.size()) eval(); // 若栈内还有元素,直接做计算
return num.top(); // 栈顶元素就是最终计算的结果
}
栈在递归调用中的应用

以斐波那契数列为例,其定义为:
F ( n ) = { F ( n − 1 ) + F ( n − 2 ) , n > 1 1 , n = 1 0 , n = 0 F(n)= \begin{cases}F(n-1)+F(n-2), & n>1 \\ 1, & n=1 \\ 0, & n=0\end{cases} F(n)=⎩ ⎨ ⎧F(n−1)+F(n−2),1,0,n>1n=1n=0
int F(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
return F(n - 1) + F(n - 2);
}
递归调用需满足以下两个条件:
- 递归表达式(递归体)
- 边界问题(递归出口)
精髓:能否将原始问题转换成属性相同但规模较小的子问题。
以F(5)为例,以下是递归调用的执行过程:

其中F(3)被调用2次,F(2)被调用3次,F(1)被调用5次,F(0)被调用3次,故递归调用效率低下,但是代码实现简单,容易理解。