第五章 基本平面图形

1 线段、射线、直线

• 线段有两个端点
• 将线段向一个方向无限延长就形成了射线
• 将线段向两个方向无限延长就形成了直线
• 经过两点有且只有一条直线
• 两点确定一条直线

2 比较线段的长短

• 两点之间线段最短
• 两点之间线段的长度，叫做这两点之间的距离

3 角

• 角由两条具有公共端点的射线组成
• 两条射线的公共端点是这个角的顶点
• 一条射线绕着它的端点旋转，当终边和始边成一条直线时，所成的角叫做平角
• 终边继续旋转，当终边和始边重合时，所成的角叫做周角
• 规定：1度 = 60分 = 3600秒；1° = 60’ = 3600’’ ；1’ = 60 ‘’

4 角的比较

• 从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分角

5 多边形和圆的初步认识

• 在一个多边形中，不相邻的两个顶点的线段叫做多边形的对角线

• 各边相等，各角也相等的多边形叫做正多边形

• 一条线段绕着它固定的一个顶点旋转一周，另一个端点所形成的图形叫做圆

• 圆上任意两点A、B间的部分叫做圆弧，简称弧，记作
  
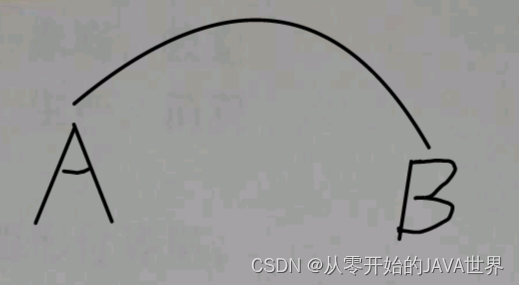
  读作"圆弧AB"或"弧AB"

• 由弧AB和经过这条弧的端点的两条半径OA,OB所组成的图像叫做扇形
  

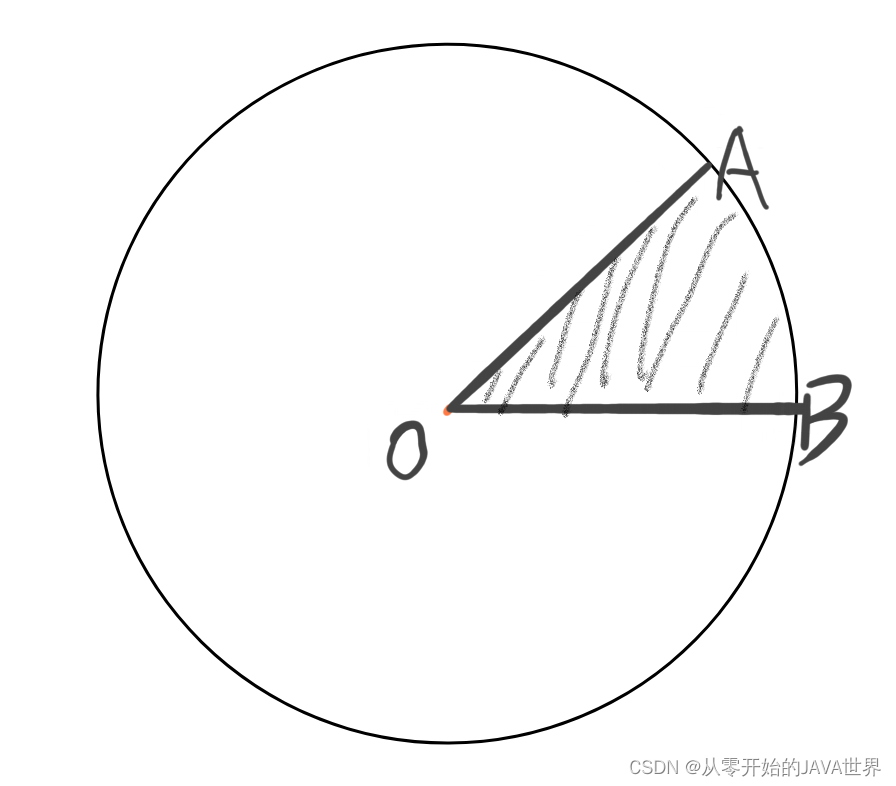
• 顶点在圆心的角叫做圆心角

第六章 整式的乘除

1 同底数幂的乘法

• 同底数幂相乘，底数不变，指数相加
• a^m ·aⁿ = a^m+n

2 幂的乘方与积的乘方

• (a^m)ⁿ = a^mn (m,n都是正整数)
• 幂的乘法，底数不变，指数相乘
• (ab)ⁿ = aⁿ b ⁿ （n是正整数）
• 积的乘方等于把积的每一个因式分别乘法，再把所得的幂相乘

3 同底数幂的除法

• a^m ÷ aⁿ = a ^m-n (a != 0 ,m,n都是正整数，且m>n)
• 同底数幂相除，底数不变，指数相减

4 零指数幂与负整数指数幂

• a ⁰ = 1（a != 0）
• a^-p = 1/a^p (a !=0,p是正整数)
• 一个不等于零的数，他的零次幂等于1，它的-p（p是正整数）次幂等于这个数的p次幂的倒数

5 整式的乘法

• 单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。
• 单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，在把所得的积相加。
• 多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

6 平方差公式

7 完全平方公式

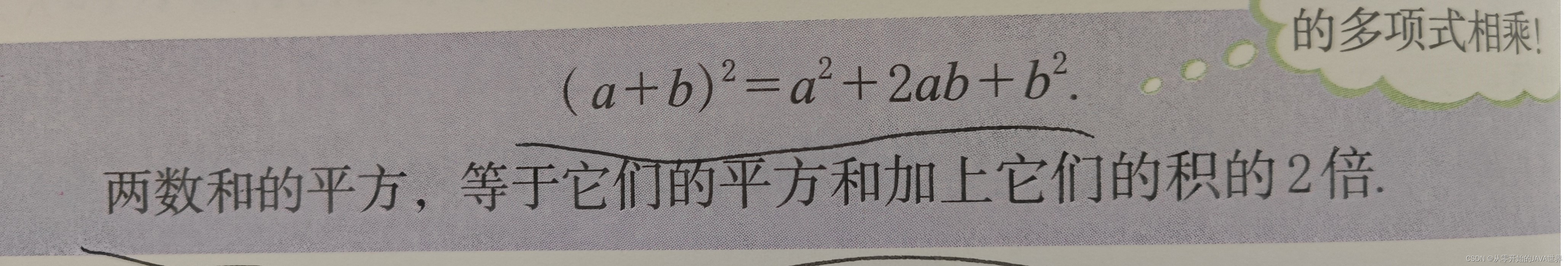
8 整式的除法

第七章 相交线与平行线

1 两条直线的位置关系

• 若两条直线在同一平面内只有一个公共点，则这两条直线为相交线
• 在同一平面内，不相交的两条直线叫做平行线
• 对顶角相等
  
• 如果两个角的和是180^°，那么称这两个角互为补角
• 如果两个角的和是90^° ，那么称这两个角互为余角
• 同角或等角的余角相等，同角或余角的补角相等
• 两条直线相交成四个角，如果有一个角是直角，那么称这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足
  
  
• 平面内过一点，有且仅有一条直线与已知直线平行
  
• 直线外一点与直线上各点连接的所有线段中，垂线段最短

2 探索直线平行的条件

• 同位角相等，两直线平行
• 过直线外一点有且仅有一条直线与这条直线平行
• 平行于同一条直线的两条直线平行
  
• 内错角相等，两直线平行
• 同旁内角互补，两直线平行

3 平行线的性质

• 两直线平行，同位角相等
• 两直线平行，内错角相等
• 两直线平行，同旁内角互补

4 用圆规做角

第八章 数据的收集与整理

1 数据的收集

2 普查和抽样调查

• 面对所有考察对象进行的全面调查叫做普查
• 其中，所要考察对象的全体称为总体
• 而组成总体的每一个考察对象称为个体
• 从总体中抽取部分个体进行调查，这种调查成为抽样调查
• 其中从总体抽取的一部分个体叫做总体的一个样本

3 数据的表示

4 统计图的选择

第九章 变量之间的关系

1 用表格表示变量之间的关系

2 用表达式表示变量之间的关系

3 用图像表示变量之间的关系