二、什么是决策树？

        决策树是一种监督式机器学习模型，它采用树状结构根据输入特征做出决策或预测。它以递归方式将数据拆分为多个子集，每个子集由所选特征的值决定，从而形成一个树状结构，其中内部节点表示决策规则，叶节点表示预测结果。该模型基于规则、可解释，适用于分类和回归任务，提供决策过程的透明表示。

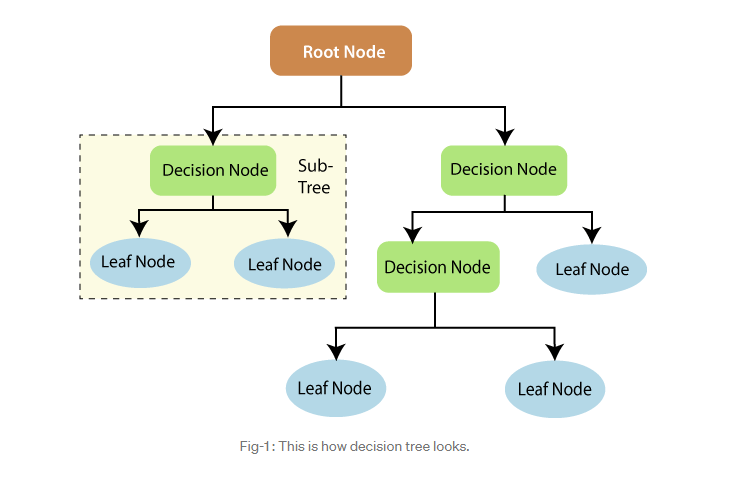
三、基本概念：

        想象一下，你必须做出一系列决定来解决问题，比如诊断疾病或选择餐馆。你从一个问题开始，每个答案都会把你引向另一个问题，直到你做出最终决定。这个过程可以可视化为一棵树，其中：

根：

起点（第一个问题）。

分支：

每个问题的可能答案。

节点：

根据问题的答案做出决定的点。

叶：

四、工作原理：

        从根开始：从整个数据集开始，然后选择最能将数据拆分为不同组的特征（问题）。

        分支： 每个答案（分支）都会导致另一个功能（问题），该特征（问题）进一步拆分数据。

        重复： 继续这个过程，直到你能做出明确的决定或预测（到达一片叶子）。

        例：

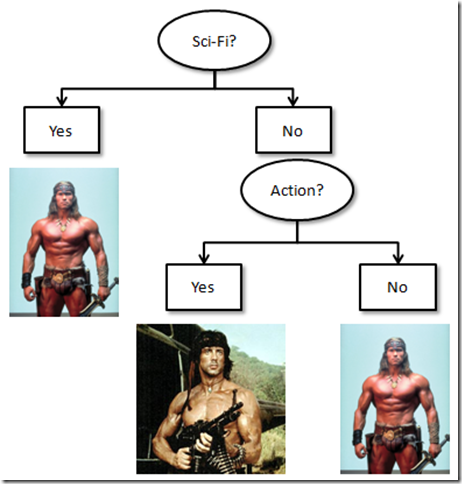
        假设您正在尝试根据动物是哺乳动物、鸟类还是爬行动物对动物进行分类。您的决策树可能如下所示：

        根源问题：动物有羽毛吗？
        是的：这是一只鸟（叶子）。
        否：转到下一个问题。

        下一个问题：动物会生下幼崽吗？
        是的：它是一种哺乳动物（叶子）。
        不：它是一种爬行动物（叶子）。

为什么有用：

           易于理解：树状结构使决策过程易于可视化和理解。

        处理不同类型的数据：可以处理数字和分类数据。

        非线性关系 ：捕获要素与目标变量之间的复杂非线性关系。

五、分类原理分析

5.1 信息熵：

        它是对一组数据的不确定性或随机性的度量。具体来说，在决策树算法中，熵用于量化基于特征的分裂前后节点的杂质。

        “熵的范围在0到1之间”，因为熵是基于概率的。

5.2 信息增益：

        信息增益衡量根据特征拆分数据集后目标变量的熵或不确定性的减少。它指示拆分后子节点与父节点相比的顺序。

5.3 基尼杂质：

        测量随机选择的元素如果根据子集中标签的分布进行随机标记，则该元素被错误标记的频率。

        基尼杂质的范围在0.5到1之间，用于二元分类：

1–1/c ，其中类（c）=2，给出 0.5

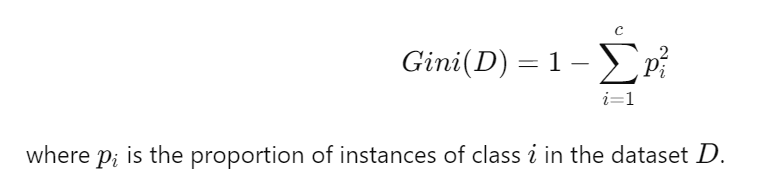
5.4 基尼系数和熵的区别：

        两者几乎相同，我们可以用它们来查找数据中的杂质，但是当涉及到更大的数据集时，基尼指数似乎更快一点，因为它计算平方和计算平方比计算“log”更快，并且对数由熵使用。这里给出一点推导：

        将熵的对数部分按泰勒展开，取第一项就成了基尼系数了。

六、对于回归决策树：

6.1 均方误差（MSE） ：

        均方误差 （MSE） 量化了 n 个实例的实际目标值 yi 与模型生成的预测值 y^i 之间的平均平方差。

6.2 使用 MSE 获得信息：

6.3 分类拆分：

        在分类任务中，目标是根据样本的特征预测样本的类标签或类别。下面是在分类决策树中拆分的示例：

        数据集：假设我们有一个花的数据集，其特征包括花瓣长度和宽度、萼片长度和宽度，以及一个指示花种的目标变量（例如，鸢尾、花色鸢尾、弗吉尼亚鸢尾）。

        示例：假设我们想根据特征“花瓣长度”拆分数据集。我们可以选择一个阈值，例如 2.5 厘米。花瓣长度小于或等于 2.5 厘米的实例转到一个子节点，花瓣长度大于 2.5 厘米的实例转到另一个子节点。

6.4 回归拆分：

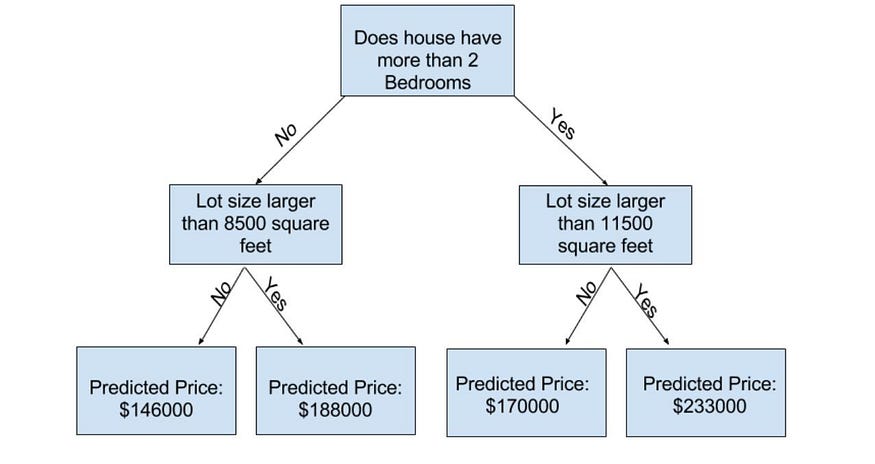
        在回归任务中，目标是根据输入特征预测连续目标变量（例如，房价、温度）。

        数据：假设我们有一个房屋数据集，其中包含卧室、浴室数量、平方英尺等特征，以及指示房屋销售价格的目标变量。

        例： 假设我们想根据特征“平方英尺”拆分数据集。我们可以选择一个阈值，例如 2000 平方英尺。面积小于或等于 2000 平方英尺的房屋将进入一个子节点，面积大于 2000 平方英尺的房屋将进入另一个子节点。

6.5 停止树的几个步骤：

1 修剪：

        修剪涉及删除树中不能提供显着预测能力或改进泛化的部分。它有助于防止树变得过于复杂并捕获数据中的噪声。

        有两种主要的修剪技术：预修剪（根据某些标准提前停止树木的生长）和修剪后（在树木完全生长后修剪）。

        成本复杂度修剪： 成本复杂度修剪，也称为最小成本复杂度修剪或 alpha 修剪，是一种用于修剪决策树以防止过度拟合的技术。它涉及通过平衡树的复杂性（大小）及其拟合训练数据的能力，从更大的、完全生长的树中选择最佳子树。修剪过程由称为复杂性参数 （α） 的超参数指导，该参数控制树大小和精度之间的权衡。

        评估修剪后的树木性能： 在单独的验证数据集上或通过交叉验证来评估修剪后的决策树的性能。测量相关指标，例如准确率、精确度、召回率、F1 分数（用于分类）或均方误差（用于回归）。

2 限制树深度：

        限制树的最大深度可防止其变得太深和太复杂。深树更容易出现过拟合，因为它们可能会捕获数据中的噪声或异常值。

        限制树的深度会鼓励模型学习更简单的决策边界，这通常会导致更好的泛化。

3 每片叶子的最小样本数 

        设置叶节点中所需的最小样本数可防止创建实例很少的节点。实例较少的节点更有可能捕获数据中的噪声或异常值。
        通过要求每片叶子的样本数量最少，树可以从更具代表性的数据子集中学习，从而降低过拟合的风险。

七、优缺点分析

7.1 优势：

1. 可解释性：决策树易于解释，因为它们表示分层树结构中的决策规则。这使得它们适合向非专家解释预测背后的原因。
2. 简单性：决策树通过将复杂的决策路径分解为一系列简单、直观的决策来模仿人类的决策过程。这种简单性使它们易于理解和可视化。
3. 处理混合数据类型：决策树可以处理数值数据和分类数据，使其适用于各种应用程序，而无需进行大量的数据预处理。
4. 非线性关系：决策树可以捕获特征与目标变量之间的非线性关系，而无需进行特征工程或转换。
5. 隐式特征选择：在训练过程中，决策树会自动选择信息量最大的特征进行拆分，从而深入了解特征的重要性。
6. 对异常值的鲁棒性：决策树对数据中的异常值和缺失值具有鲁棒性，因为它们不依赖于基于距离的指标。

7.2 缺点

1. 过拟合 ：决策树容易出现过拟合，尤其是当允许其增长到过深或过复杂时。修剪和设置最大深度等技术对于缓解过拟合是必要的。
2. 不稳定性：训练数据的微小变化可能导致决策树的显著差异，使它们成为不稳定的模型。像随机森林这样的集成方法可以通过聚合多个决策树来帮助解决这个问题。
3. 偏向优势类：在类分布不平衡的分类任务中，决策树倾向于偏向优势类，导致少数类的性能欠佳。
4. 高方差：决策树具有高方差，这意味着它们对训练数据的变化很敏感，如果没有适当的正则化，可能无法很好地泛化到看不见的数据。
5. 有限的表达能力：尽管决策树能够捕获非线性关系，但与神经网络或梯度提升机等更复杂的模型相比，决策树的表现力有限。
6. 贪婪的本质：决策树在训练过程中使用贪婪的、自上而下的方法，这可能并不总是导致全局最优分裂，并可能导致次优树。

八、结论

        总之，决策树是多功能且功能强大的机器学习模型，具有许多优势，包括简单性、可解释性和灵活性。由于它们能够处理数值和分类数据，以及对决策过程的直观表示，它们被广泛用于各个领域的分类和回归任务。

        决策树根据简单的决策规则将特征空间划分为多个区域，使其易于理解和解释。它们提供了对预测的最重要特征的见解，并为决策过程提供了透明度，这对于可解释性至关重要的应用至关重要，例如医疗保健或金融。

        “决策树”的旅程充满了热情和奉献精神，致力于分享对不断发展的科技世界的知识和见解。得到以下机构的支持和认可