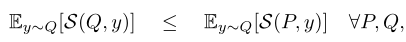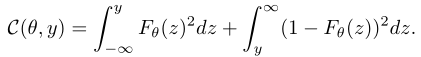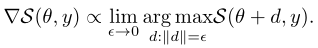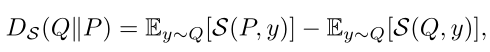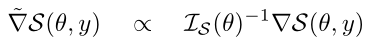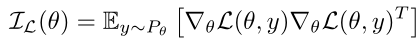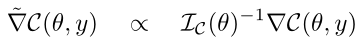目录
- 1、文章贡献
- 2、评分规则
- 3、自然梯度
- 4、自然梯度提升算法NGBoost

1、文章贡献
由吴恩达团队提出的NGBoost是一种通过梯度提升进行概率预测的算法,与经典的回归模型返回一个点估计结果不同,概率回归模型返回全概率分布,将条件分布的参数视为多参数提升算法的目标,将梯度提升推广到概率回归,允许对不确定性进行预测估计。
2、评分规则
- 假设一个概率分布Pθ(y|x),与点估计中观测值通过损失函数比较相类似,概率回归中使用评分规则将估计的概率分布与观测数据比较。
评分规则S将概率分布P和观测值y作为输入,记为S(P,y)。当且仅当:
其中Q是y的真实分布,P是其他任何分布。- 最常用的评分规则是对数分数L,当最小化时MLE表示为:
- 另一个代替规则是CRPS,定义为:
3、自然梯度
- 采用标准的梯度下降方法,通过在每个点x上沿分数相对于参数的负梯度下降,来找到最小化评分规则的参数。
在梯度的该方向上无限小的移动参数将最大程度增加评分规则:
- 每一个适当的评分规则都会产生一个散度,可以作为分布空间中的局部距离度量。在第一个评分规则满足的不等式中,右侧关于左侧的超额分数是评分规则引起的散度,定义为:
可以解释为一个分布Q到另一个分布P差异的度量。其中MLE评分规则引发Kullback-Leibler散度;CRPS评分规则引发L²散度。
(散度KL和散度L²对Q和P的参数化方式是不变的,虽然散度在一般情况下是不对称的,但对于参数的微小变化几乎是对称的,可以作为局部距离度量。当这样使用时,散度会产生一个统计流形,其中统计流中的每个点对应一个概率分布)- 广义自然梯度是黎曼空间中上升最陡的方向,对参数化不变,定义为:
- 如果我们求解相应的优化问题,就得到了以下形式的自然梯度:
其中Ⅰs(θ)是θ处统计流形的黎曼度量- 选择评分规则为MLE即令S=L,求解优化问题得到:
其中ⅠL(θ)是关于Pθ的费歇尔信息量,定义为:
- 同样地,选择评分规则为CRPS即令S=C,求解优化问题得到:
其中Ⅰc(θ)是使用L²作为局部距离度量的统计流形的黎曼度量,定义为:
使用自然梯度学习参数使优化问题不受参数化的影响,并导致更有效和稳定的学习动态。
考虑在概率回归中调整梯度提升来预测参数θ。
4、自然梯度提升算法NGBoost
算法有三个模块化组件:
- 基学习器f
- 参数概率分布Pθ
- 评分规则S
- 对新输入x的预测 y|x 以条件概率分布Pθ的形式进行,其中参数θ由M个基学习器的输出和初始值的加法组合获得。注意θ完全决定了概率预测 y|x 。
(例如对于参数μ和logσ的正态分布,每个基学习器f将x作为输入,预测输出用特定的比例因子ρ缩放,学习率为η)
- 学习算法首先估计初始值θ(0),使它最小化评分规则对所有训练实例的响应变量的和,本质上是拟合y的边际分布。
- 对于M颗树的每次迭代m,算法计算对于每个实例i下,评分规则S相对于该阶段下的预测参数θi(m-1)的自然梯度gi(m),本次迭代的基学习器预测拟合每个实例xi对应的梯度gi(m)。
- 输出通过缩放因子ρ缩放,选择缩放因子来通过线性的形式沿着梯度方向将整体真实评分规则损失最小化。
- 一旦缩放因子ρ确定,预测每个实例的参数将通过每个θi(m-1)的负缩放梯度相加更新为θi(m)。