兑换零钱(一)_牛客题霸_牛客网

兑换零钱(二)_牛客题霸_牛客网

---

兑换零钱(一)_牛客题霸_牛客网

描述

给定数组arr，arr中所有的值都为正整数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，再给定一个aim，代表要找的钱数，求组成aim的最少货币数。

如果无解，请返回-1.

数据范围：数组大小满足 0≤n≤100000≤n≤10000 ， 数组中每个数字都满足 0<val≤100000<val≤10000，0≤aim≤50000≤aim≤5000

要求：时间复杂度 O(n×aim)O(n×aim) ，空间复杂度 O(aim)O(aim)。

 【解法一】贪心策略为了达到使用纸币次数最少的情况，所以应该尽量使用更大的纸币来进行兑换，但是又存在一些缺点，就是存在一种情况如下：答案返回为14，但是用13张365面值的纸币再用一张 4976-13*365=231，面对231选择一张181之后剩了50没有可以继续划分的情况了

[357,322,318,181,22,158,365],   4976

写这篇博客更多想表达的是一种贪心的思想吧，因为贪心具有局限性，很容易就不能完成这种关于最大值与最小值的问题。

class Solution {
public:
    int minMoney(vector<int>& arr, int aim) {
        // 从大到小排序
        sort(arr.begin(), arr.end(), greater());
        int cnt = 0; // 纸币张数
        for(auto e : arr)
        {
            int c = aim / e;    //当前纸币可以换取得最大张数
            cnt += c;       
            aim -= c*e;
        }
        if(aim != 0)return -1;
        return cnt;
    }
};

【解法二】动态规划，这个注意初始化，当题目要求的是最小个数的话，一般初始化为一个max大数，然后每次dp转移时取min

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        int n = coins.size();
        if(amount < 1)return 0;
        vector<int> dp(amount+1, amount+1);
        dp[0] = 0;
        for(int i = 0; i < n; i++)
        {
            for(int j = coins[i]; j <= amount; j++)
            {
                dp[j] = min(dp[j], dp[j-coins[i]]+1);
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
};

兑换零钱(二)_牛客题霸_牛客网

给定一个整数数组 nums 表示不同数额的硬币和一个正整数 target 表示总金额，请你计算并返回可以凑出总金额的的组合数。如果凑不出 target 则返回 0。

数据范围：数组长度满足 1≤n≤300 1≤n≤300  ，数组中的数和 target 大小满足 1≤val≤5000 1≤val≤5000 

 

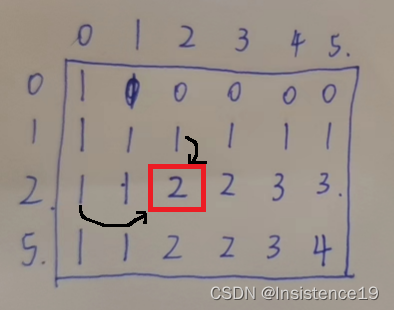
由上表结合完全背包可以推出，金额个数 F(i,j) = F(i-1, j)+F(i, j-nums[i])之和

class Solution {
public:
    int change(int target, vector<int>& nums) {
        // write code here
        int n = nums.size();
        vector<int> dp(target+1, 0);
        dp[0] = 1;
        for(int i = 0; i < n; i++)
        {
            for(int j = nums[i]; j <= target; j++)
            {
                dp[j] = dp[j] + dp[j-nums[i]];
            }
        }
        return dp[target];
    }
};