Problem: 226. 翻转二叉树
文章目录
- 题目描述
- 思路
- 复杂度
- Code
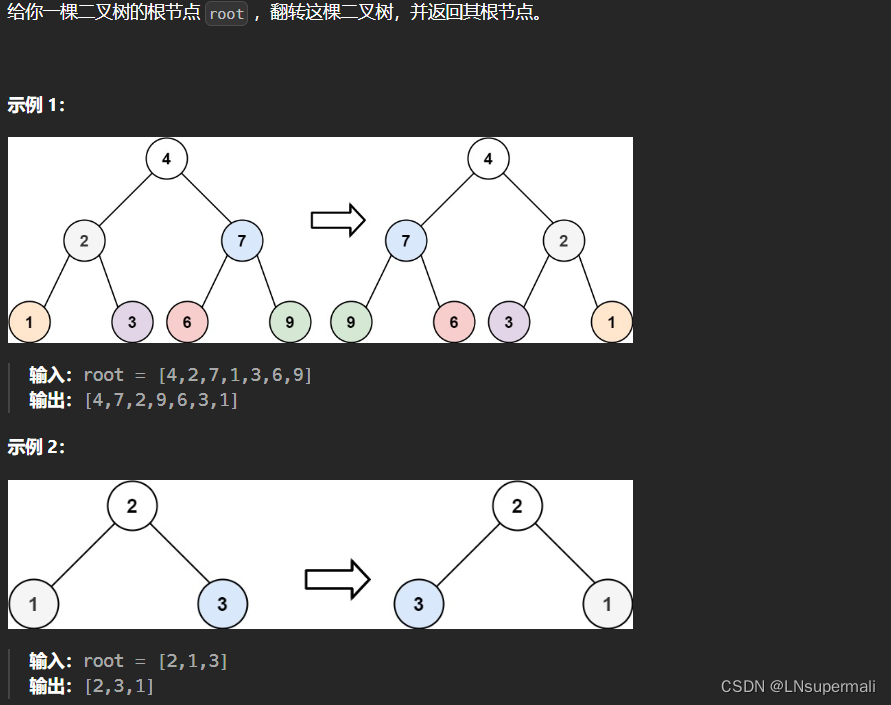
题目描述
思路
涉及二叉树的递归解法时往往需要考虑两种思路:
1.在递归遍历时执行题目需要的具体要求;
2.将一个大问题分解为多个小子问题
具体到本体:
思路1:遍历
先序遍历+基本的交换操作
思路2:问题分解
将翻转一棵二叉树分解为翻转根节点的左右子树,再分解为翻转左右子树的左右子树…一直分解到叶子节点时,再在回退的过程中执行交换操作,即需要利用到二叉树的后序遍历
复杂度
思路1:
时间复杂度:
O ( n ) O(n) O(n);其中 n n n为二叉树节点的个数
空间复杂度:
O ( n ) O(n) O(n)
思路2:
时间复杂度:
O ( n ) O(n) O(n)
空间复杂度:
O ( n ) O(n) O(n)
Code
思路1:
class Solution {
/**
* Invert Binary Tree(Recursive traversal)
*
* @param root The root node of binary tree
* @return TreeNode
*/
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
traverse(root);
return root;
}
/**
* Recursive implementation function
*
* @param root The root node of binary tree
*/
private void traverse(TreeNode root) {
if (root == null) {
return;
}
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
traverse(root.left);
traverse(root.right);
}
}
思路2:
class Solution {
/**
* Invert Binary Tree(Break down the problem)
*
* @param root The root node of binary tree
* @return TreeNode
*/
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode leftNode = invertTree(root.left);
TreeNode rightNode = invertTree(root.right);
root.left = rightNode;
root.right = leftNode;
return root;
}
}