上一篇博客我们使用闭散列的方式实现了 Hash,其实在STL库unordered_set、unordered_map中底层是开散列的方式实现的Hash,所以,本篇博客就再使用开散列的方式实现Hash,并将unordered_set、unordered_map进行封装。
目录
一、开散列
1.1 开散列的概念
1.2 开散列结构
1.3 Insert 插入
1.4 Find 查找
1.5 Insert 扩容
1.6 Erase 删除
1.7 析构函数
1.8 测试接口
1.9 性能测试
二、封装
2.1 封装内部结构
2.2 实现接口
三、迭代器
3.1 迭代器的定义
3.2 常用接口
3.3 迭代器++
3.4 begin()、end()
3.5 find的改动
3.6 下标访问[ ]重载
四、源代码与测试用例
4.1 底层HashTable
4.2 unordered_set/map
4.3 测试用例
一、开散列
1.1 开散列的概念
开散列法又称链地址法(拉链法、哈希桶),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个字集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。

1.2 开散列结构
首先我们要使用vector来存储每个链表的节点,然后每个节点中有数据域和指针next域。然后我们可以将HashNode的构造函数写一下,使用pair类型构造处一个HashNode。
template <class K, class V>
struct HashNode
{
HashNode(const pair<K, V>& kv)
:_kv(kv), _next(nullptr)
{
}
pair<K, V> _kv;
HashNode<K, V>* _next;
};
template <class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:
typedef HashNode<K, V> Node;
private:
vector<Node*> _table;
size_t _size = 0;
};1.3 Insert 插入
首先我们实现插入的主逻辑,然后对其进行逐步优化。
我们根据 kv 创建一个节点,然后根据仿函数进行取模求出映射位置,然后进行链表的头插。
bool Insert(const pair<K, V>& kv)
{
Hash hash;
size_t hashi = hash(kv.first) % _table.size();
//头插
Node* newNode = new Node(kv);
newNode->_next = _table[hashi];
_table[hashi] = newNode;
++_size;
return true;
}像哈希表中插入数据首先要保证数据的唯一性,所以我们要先进行去重处理,此时我们顺带实现Find函数。
1.4 Find 查找
根据key值求出映射位置,如果该位置不为空,则进行链表的遍历,如果找到key值,则返回cur节点,如果找不到则向后遍历,直到cur为空。
Node* Find(const K& key)
{
if (_table.size() == 0) return nullptr;
Hash hash;
size_t hashi = hash(key) % _table.size();
//向桶中进行查找
Node* cur = _table[hashi];
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}1.5 Insert 扩容
插入的主逻辑实现了,去重判断也实现了,接下来就是表的扩容。
如果哈希表的大小为0或达到了哈希的装载因子,则要进行扩容。
我们看一下STL库中负载因子控制的多少:

STL库中设计的负载因子为:当表中插入的元素个数>哈希表的大小,即负载因为为1的时候进行扩容,将表的大小扩容到 next_size.
扩容的挪动数据要注意,因为开散列的每个桶上的数据个数不同。进行扩容后,桶中每个元素都可能映射到不同的新位置处,所以我们不能像闭散列那样复用Insert,要重新将结点链接到新表中。
挪动时要让原表中的结点一个一个链接到新表中:
//扩容 --- 如果插入的数据等于表的大小
if (_size == _table.size())
{
size_t newSize = _table.size() == 0 ? 10 : _table.size() * 2;
vector<Node*> newTable;
newTable.resize(newSize, nullptr);
//将旧表中的节点移动映射到新表
Hash hash;
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
size_t hashi = hash(cur->_kv.first) % _table.size();
cur->_next = newTable[hashi];
newTable[hashi] = cur;
cur = next;
}
//将旧表i位置处结点清空
_table[i] = nullptr;
}
_table.swap(newTable);
}
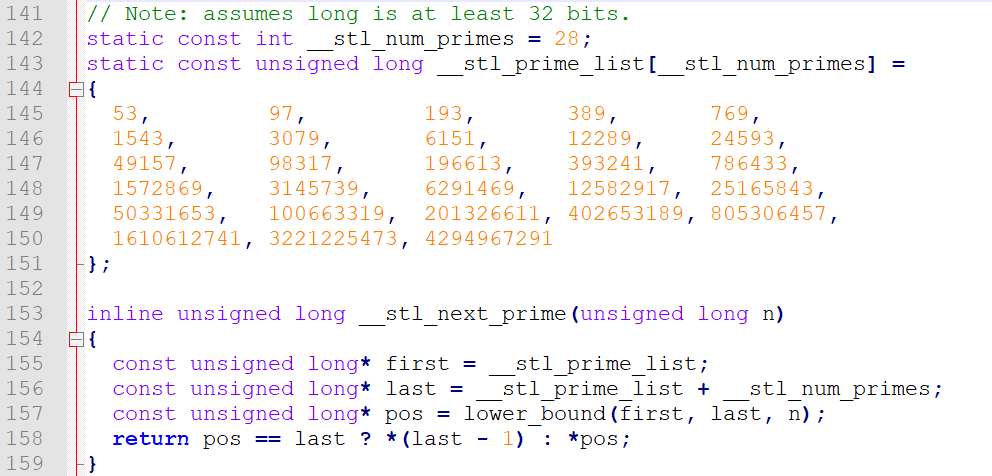
发现源码中进行扩容时调用了 next_size 函数,扩容直接将size乘以2不就行了吗,为什么要特殊计算 size ?
因为hash表的大小最好是素数,如果是素数,映射的结果冲突几率就小,因为非素数因子多,进行映射后相同位置冲突大。将hash表的大小设计为素数后,其实就可以做到hash表中个别桶的冲突次数过多而过分的大。
详细可以看这篇文章:算法分析:哈希表的大小为何是素数
现在我们也添加这个功能:
库中使用lower_bound(返回第一个大于等于n的下标)/upper_bound(返回第一个大于n的下标),其实直接使用for循环遍历就行了.
inline size_t __stl_next_prime(size_t n)
{
static const size_t __stl_num_primes = 28;
static const size_t __stl_prime_list[__stl_num_primes] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
//取下一次扩容的大小:
for (size_t i = 0; i < __stl_next_prime; i++)
{
if (__stl_prime_list[i] > n)
return __stl_prime_list[i];
}
return (size_t)-1;
}1.6 Erase 删除
虽然我们实现了Find函数,但是单单使用Find是无法完成删除功能的。
例如下面这种情况,单链表删除中间结点我们还需要知道 prev 结点。

bool Erase(const K& key)
{
if (_table.size() == 0) return false;
Hash hash;
size_t hashi = hash(key) % _table.size();
Node* pre = nullptr;
Node* cur = _table[hashi];
while (cur)
{
if (cur->_kv.first == hash(key))
{
//如果删除的是链中第一个元素 --- 即头删
if (pre == nullptr)
{
_table[hashi] = cur->_next;
}
//2.中间删除
else
{
pre->_next = cur->_next;
}
delete cur;
--_size;
return true;
}
pre = cur;
cur = cur->_next;
}
return false;
}1.7 析构函数
注意了,当哈希表生命周期结束后会调用析构函数,我们使用的vector会自动释放表中的内容,可是vector中存放的是链表,我们释放时还要对桶(链表)进行释放,所以我们要手动写一个析构函数。
~HashTable()
{
for (size_t i = 0; i < _table.size(); ++i)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_table[i] = nullptr;
}
}1.8 测试接口
接下来我们写一些hash表的测试接口,以便下面性能测试使用。
//表的长度
size_t BucketSize()
{
return _table.size();
}
//数据个数
size_t Size()
{
return _size;
}
//桶的数量
size_t BucketNum()
{
size_t Num = 0;
for (size_t i = 0; i < BucketSize(); i++)
{
if (_table[i]) Num++;
}
return Num;
}
//最长的桶
size_t MaxBucketLenth()
{
size_t Max_len = 0;
size_t temp = 0;
for (size_t i = 0; i < BucketSize(); i++)
{
if (_table[i])
{
size_t len = 1;
Node* cur = _table[i]->_next;
while (cur)
{
len++;
cur = cur->_next;
}
if (len > Max_len)
{
Max_len = len;
temp = i;
}
}
}
printf("Max_len_i:[%u]\n", temp);
return Max_len;
}1.9 性能测试
void TestHT()
{
int n = 18000000;
vector<int> v;
v.reserve(n);
srand((unsigned int)time(0));
for (int i = 0; i < n; ++i)
{
v.push_back(rand()+i); // 重复少
//v.push_back(rand()); // 重复多
}
size_t begin1 = clock();
HashTable<int, int> ht;
for (auto e : v)
{
ht.Insert(make_pair(e, e));
}
size_t end1 = clock();
cout << "数据个数:" << ht.Size() << endl;
cout << "表的长度:" << ht.BucketSize() << endl;
cout << "桶的个数:" << ht.BucketNum() << endl;
cout << "平均每个桶的长度:" << (double)ht.Size() / (double)ht.BucketNum() << endl;
cout << "最长的桶的长度:" << ht.MaxBucketLenth() << endl;
cout << "负载因子:" << (double)ht.Size() / (double)ht.BucketSize() << endl;
}
发现,将哈希表的大小设置为素数后,即使负载因子到了0.9,最长的桶也不过才是 2。所以hash表的查找效率为O(1)。
接下来我们对比红黑树和hash表其查找效率(查找1千万个数据)

哈希表插入效率较低,是因为扩容挪动数据非常消耗时间。
接下来我们使用set、onordered_set底层对应的就是红黑树和hash表,向其中插入1千万的随机数,对比其性能,并对onordered_set进行直接插入和提前扩容再进行插入的效率对比。

测试代码如下:
void test_op()
{
int n = 10000000; //1千万个数据
vector<int> v;
v.reserve(n);
srand((unsigned int)time(0));
for (int i = 0; i < n; ++i)
{
//v.push_back(i);
v.push_back(rand()^ 1311 * 144+i);
}
size_t begin1 = clock();
set<int> s;
for (auto e : v)
{
s.insert(e);
}
size_t end1 = clock();
size_t begin2 = clock();
unordered_set<int> us;
us.reserve(n);
for (auto e : v)
{
us.insert(e);
}
size_t end2 = clock();
cout << "有效数据个数:" << s.size() << endl;
cout << "\nInsert 插入:" << endl;
cout << "set : " << end1 - begin1 << endl;
cout << "unordered_set : " << end2 - begin2 << endl;
size_t begin3 = clock();
for (auto e : v)
{
s.find(e);
}
size_t end3 = clock();
size_t begin4 = clock();
for (auto e : v)
{
us.find(e);
}
size_t end4 = clock();
cout << "\nFind 查找:" << endl;
cout << "set :" << end3 - begin3 << endl;
cout << "unordered_set :" << end4 - begin4 << endl;
size_t begin5 = clock();
for (auto e : v)
{
s.erase(e);
}
size_t end5 = clock();
size_t begin6 = clock();
for (auto e : v)
{
us.erase(e);
}
size_t end6 = clock();
cout << "\nErase 删除:" << endl;
cout << "set erase:" << end5 - begin5 << endl;
cout << "unordered_set erase:" << end6 - begin6 << endl;
}
以上就是我们hash开散列的基本实现了,实现了以上功能我们就可以封装unordered_map/unordered_set了。
二、封装
2.1 封装内部结构
首先是改变HashTable中每个结点存储的数据类型,如unordered_set中存放的是key,unordered_map中存放的是pair类型,所以我们将结点中存储的类型改为T,如果是set,T对应就是key,如果是map,那T就对应pair结构。
template <class T>
struct HashNode
{
HashNode(const T& data)
:_data(data), _next(nullptr)
{}
T _data;
HashNode<T>* _next;
};所以,Insert插入的类型也应改为T模板类型,在使用到类型中的值时,使用仿函数取出该比较的数据。
然后我们就来编写unordered_set(map)类
unordered中底层就是调用我们写的HashTable,所以直接使用HashTable定义成员变量,并传入模板参数。(以下简写的set、map都对应的Hash方法实现的unordered_set(map))
注意,因为set是Key模型,设置一个模板参数即可;而map是KV模型,需要设置两个模板参数对应pair的中的两个数据类型。所以,在底层我们统统传入HashTalbe两个模板参数,并以第二个模板参数为准决定底层存储什么类型,如果是set,就使用仿函数取出key,如果是map就使用仿函数取出pair.first。
所以,在传入参数前我们要先编写好仿函数set(map)KeyOfT,以便于底层取出数据。
//**** set *********
template<class K, class Hash = HashFunc<K>>
class unordered_set
{
public:
private:
struct setKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
//两个模板参数都传入K
HashTable<K, K, Hash, setKeyOfT> _ht;
};
//**** map *********
template<class K, class V, class Hash = HashFunc<K>>
class unordered_map
{
public:
private:
//让HashTable取出pair中的K --- 内部类
struct mapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
HashTable<K, pair<K, V>, Hash, mapKeyOfT> _ht;
};2.2 实现接口
接下来就是为我们封装的map、set 设计成员函数,其实我们只是封装了一层,本质还是调用HashTable中的Insert、Erase等函数。
// ****** set ********
bool insert(const K& kv)
{
return _ht.Insert(kv);
}
bool erase(const K& kv)
{
return _ht.Erase(kv);
}
// ****** map ********
bool insert(const pair<K, V>& kv)
{
return _ht.Insert(kv);
}
bool erase(const K& k)
{
return _ht.Erase(k);
}注意,Insert、Erase的底层中,涉及到key值操作的,我们要进行使用两层仿函数进行取值。
接下来我们简单来测试一下代码:

三、迭代器
3.1 迭代器的定义
在HashTable中有迭代器的接口(begin()、end()),而迭代器中也会使用到HashTable的结构,所以,在实现迭代器之前我们要先进行HashTable的声明(注意:模板类的声明要加上模板参数一起声明)。
我们来看看源码中迭代器是如何定义的

接下来是我们的定义:
//前置声明
template <class K, class T, class Hash, class keyOfT>
class HashTable;
template<class K, class T, class Hash, class keyOfT>
class __Hash_Iteartor
{
public:
typedef HashNode<T> Node;
typedef HashTable<K, T, Hash, keyOfT> HT;
typedef __Hash_Iteartor<K, T, Hash, keyOfT> Self;
__Hash_Iteartor(Node* node, HT* pht)
:_node(node), _pht(pht)
{}
__Hash_Iteartor()
{}
private:
//成员变量
Node* _node; //指向结点
HT* _pht; //指向当前表
};3.2 常用接口
接下来实现一些常用的接口:
T& operator*()
{
return _node->_data;
}
T* operator->()
{
return &_node->_data;
}
bool operator!=(const Self& self)
{
return _node != self._node;
}
bool operator==(const Self& self)
{
return _node == self._node;
}3.3 迭代器++
STL中迭代器++的实现:

思路如下:
- 判断_node的_next是否存在存在结点,如果存在直接让_node = _node->_next即可
- 如果不存在结点,则当前桶遍历结束,要寻找下一个有数据的桶。
- 根据_node中的data域求出映射位置,然后从映射位置向后遍历哈希表,直到talbe[i]处有数据,有数据则跳出循环
- 当 i 等于哈希表的大小,则表示不存在下一个数据,则将_node赋值为nullptr
- 返回*this,即返回当前对象。
Self& operator++()
{
//在当前桶中进行++
if (_node->_next)
{
_node = _node->_next;
}
else //找下一个有效的桶
{
Hash hash;
keyOfT kft;
size_t i = hash(kft(_node->_data)) % _pht->_table.size();
for (i += 1; i < _pht->_table.size(); i++)
{
if (_pht->_table[i])
{
_node = _pht->_table[i];
break;
}
}
//如果不存在有数据的桶
if (i == _pht->_table.size())
_node = nullptr;
}
return *this;
}注意,此时我们使用了哈希表,具体访问了其中的元素,所以我们要让迭代器作为HashTable的友元类(也要带上模板参数进行声明噢)。

3.4 begin()、end()
begin就是返回HashTable中第一个存储了数据的桶。如果表中没有存储数据,直接返回end(),而end()迭代器中的_node为nullptr构造的。
typedef __Hash_Iteartor<K, T, Hash, keyOfT> iterator;
iteratorbegin()
{
for (size_t i = 0; i < _table.size(); i++)
{
if (_table[i])
return iterator(_table[i], this);
}
return end();
}
iterator end()
{
return iterator(nullptr, this);
}然后我们就可以在map、set添加其接口了。

注意,这里要使用typename,要指明iterator是HashTable中的一个类型,而不是变量。
3.5 find的改动
find中,我们返回是直接返回迭代器,在return的地方使用匿名对象进行返回即可。

3.6 下标访问[ ]重载
如果要实现map中的下标访问操作符重载,我们要对Insert进行改造,让其返回值为pair结构,其中first为迭代器,second为bool类型,表示插入成功与否(虽然不改变也能实现)。


Insert的改动完成后,接下来就可以在map中添加 [] 下标访问操作符重载了。
V& operator[](const K& key)
{
pair<iterator, bool> ret = _ht.Insert(make_pair(key, V()));
return ret.first->second;
}接下来就可以测试一下
以下这段代码即检测了 [ ]重载,也检测了迭代器,以及find、insert和两个仿函数。

注意,在源码中,其实还有一个仿函数模板参数。

这个仿函数的功能是,如果我们存储的是日期类的指针(Date*),按正常比较会根据指针中存放的地址大小进行比较,我们可以传入自定义传入这个仿函数,就可以做到即使传入的是Date*,也可以按照Date*指向的内容,根据日期进行排序。
一个类型K去做 set 和 unordered_set 的模板参数有什么要求?
答:set :
set要求支持能进行小于号比较,或者显示提供比较的仿函数
unordered_set:
要求K类型对象能转化为整形取模,或提供能装化为整形的仿函数
K类型对象要支持等于比较,或提供等于比较的仿函数 (set有小于,就可以通过左小右大的方式找到数据;而unordered_set 会出现冲突,使用key值只能找到映射的桶,遍历桶的时候,就需要进行等于比较了)
四、源代码与测试用例
4.1 底层HashTable
template<class K>
struct HashFunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
template<>
struct HashFunc<string>
{
size_t operator()(const string& key)
{
size_t val = 0;
for (auto ch : key)
val = val * 131 + ch;
return val;
}
};
template <class T>
struct HashNode
{
HashNode(const T& data)
:_data(data), _next(nullptr)
{}
T _data;
HashNode<T>* _next;
};
// 对哈希表进行前置声明
template <class K, class T, class Hash, class keyOfT>
class HashTable;
template<class K, class T, class Hash, class keyOfT>
class __Hash_Iteartor
{
public:
typedef HashNode<T> Node;
typedef HashTable<K, T, Hash, keyOfT> HT;
typedef __Hash_Iteartor<K, T, Hash, keyOfT> Self;
__Hash_Iteartor(Node* node, HT* pht)
:_node(node), _pht(pht)
{}
__Hash_Iteartor()
:_node(nullptr), _pht(nullptr)
{}
T& operator*()
{
return _node->_data;
}
T* operator->()
{
return &_node->_data;
}
Self& operator++()
{
//在当前桶中进行++
if (_node->_next)
{
_node = _node->_next;
}
else //找下一个有效的桶
{
Hash hash;
keyOfT kft;
size_t i = hash(kft(_node->_data)) % _pht->_table.size();
for (i += 1; i < _pht->_table.size(); i++)
{
if (_pht->_table[i])
{
_node = _pht->_table[i];
break;
}
}
//如果不存在有数据的桶
if (i == _pht->_table.size())
_node = nullptr;
}
return *this;
}
bool operator!=(const Self& self)
{
return _node != self._node;
}
bool operator==(const Self& self)
{
return _node == self._node;
}
private:
//成员
Node* _node; //指向结点
HT* _pht; //指向当前表
};
template <class K, class T, class Hash, class keyOfT>
class HashTable
{
public:
typedef HashNode<T> Node;
//将迭代器设为友元
template<class K, class T, class Hash, class keyOfT>
friend class __Hash_Iteartor;
typedef __Hash_Iteartor<K, T, Hash, keyOfT> iterator;
iterator begin()
{
for (size_t i = 0; i < _table.size(); i++)
{
if (_table[i])
return iterator(_table[i], this);
}
return end();
}
iterator end()
{
return iterator(nullptr, this);
}
//析构要进行特殊处理,遍历整个表,再删除桶中的数据。
~HashTable()
{
for (size_t i = 0; i < _table.size(); ++i)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_table[i] = nullptr;
}
}
inline size_t __stl_next_prime(size_t n)
{
static const size_t __stl_num_primes = 28;
static const size_t __stl_prime_list[__stl_num_primes] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
//取下一次扩容的大小:
for (size_t i = 0; i < __stl_num_primes; i++)
{
if (__stl_prime_list[i] > n)
return __stl_prime_list[i];
}
return (size_t)-1;
}
pair<iterator, bool> Insert(const T& data)
{
Hash hash;
keyOfT koft;
//去重
iterator ret = Find(koft(data));
if (ret != end())
{
return make_pair(ret, false);
}
//扩容 --- 如果插入的数据等于表的大小
if (_size == _table.size())
{
//size_t newSize = _table.size() == 0 ? 10 : _table.size() * 2;
vector<Node*> newTable;
size_t newSize = __stl_next_prime(_table.size());
newTable.resize(newSize, nullptr);
//将旧表中的节点移动映射到新表
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
size_t hashi = hash(koft(cur->_data)) % newSize;
cur->_next = newTable[hashi];
newTable[hashi] = cur;
cur = next;
}
//将旧表i位置处结点清空
_table[i] = nullptr;
}
_table.swap(newTable);
}
size_t hashi = hash(koft(data)) % _table.size();
//头插
Node* newNode = new Node(data);
newNode->_next = _table[hashi];
_table[hashi] = newNode;
++_size;
return make_pair(iterator(newNode, this), true);
}
iterator Find(const K& key)
{
if (_table.size() == 0) return end();
Hash hash;
keyOfT koft;
size_t hashi = hash(key) % _table.size();
//向桶中进行查找
Node* cur = _table[hashi];
while (cur)
{
if (koft(cur->_data) == key)
{
return iterator(cur, this);
}
cur = cur->_next;
}
return end();
}
//单链表不能直接找到该节点并删除
bool Erase(const K& key)
{
if (_table.size() == 0) return false;
Hash hash;
keyOfT koft;
size_t hashi = hash(key) % _table.size();
Node* pre = nullptr;
Node* cur = _table[hashi];
while (cur)
{
if (koft(cur->_data) == hash(key))
{
//如果删除的是链中第一个元素 --- 即头删
if (pre == nullptr)
{
_table[hashi] = cur->_next;
}
//2.中间删除
else
{
pre->_next = cur->_next;
}
delete cur;
--_size;
return true;
}
pre = cur;
cur = cur->_next;
}
return false;
}
//表的长度
size_t BucketSize()
{
return _table.size();
}
//数据个数
size_t Size()
{
return _size;
}
//桶的数量
size_t BucketNum()
{
size_t Num = 0;
for (size_t i = 0; i < BucketSize(); i++)
{
if (_table[i]) Num++;
}
return Num;
}
//最长的桶
size_t MaxBucketLenth()
{
size_t Max_len = 0;
size_t temp = 0;
for (size_t i = 0; i < BucketSize(); i++)
{
if (_table[i])
{
size_t len = 1;
Node* cur = _table[i]->_next;
while (cur)
{
len++;
cur = cur->_next;
}
if (len > Max_len)
{
Max_len = len;
temp = i;
}
}
}
printf("Max_len_i:[%u]\n", temp);
return Max_len;
}
void Print_map()
{
cout << "Print_map:" << endl;
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
cout << "i:" << i << " [" << cur->_data.first << " " << cur->_data.second << "] " << endl;
cur = cur->_next;
}
}
}
void Print_set()
{
cout << "Print_set:" << endl;
for (int i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
cout << "i:" << i << " [" << cur->_data << "] " << endl;
cur = cur->_next;
}
}
}
private:
vector<Node*> _table;
size_t _size = 0;
};
4.2 unordered_set/map
unordered_set:
template<class K, class Hash = HashFunc<K>>
class unordered_set
{
public:
struct setKeyOfT;
typedef typename Brant::HashTable<K, K, Hash, setKeyOfT>::iterator iterator;
iterator begin()
{
return _ht.begin();
}
iterator end()
{
return _ht.end();
}
pair<iterator, bool> insert(const K& kv)
{
return _ht.Insert(kv);
}
bool erase(const K& kv)
{
return _ht.Erase(kv);
}
void print()
{
_ht.Print_set();
}
private:
struct setKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
HashTable<K, K, Hash, setKeyOfT> _ht;
};unordered_map:
template<class K, class V, class Hash = HashFunc<K>>
class unordered_map
{
public:
struct mapKeyOfT;
typedef typename Brant::HashTable<K, pair<K, V>, Hash, mapKeyOfT>::iterator iterator;
iterator begin()
{
return _ht.begin();
}
iterator end()
{
return _ht.end();
}
pair<iterator, bool> insert(const pair<K, V>& kv)
{
return _ht.Insert(kv);
}
bool erase(const K& k)
{
return _ht.Erase(k);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = _ht.Insert(make_pair(key, V()));
return ret.first->second;
}
void print()
{
_ht.Print_map();
}
private:
//取出pair中的K值 --- 内部类
struct mapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
HashTable<K, pair<K, V>, Hash, mapKeyOfT> _ht;
};4.3 测试用例
封装测试:
void test_unordered01()
{
Brant::unordered_map<int, int> mp1;
mp1.insert({ 1,1 });
mp1.insert({ 54,54 });
mp1.insert({ 2,2 });
mp1.insert({ 3,3 });
mp1.insert({ 4,4 });
mp1.insert({ 6,6 });
mp1.insert({ 6,6 });
mp1.print();
cout << "Erase:---------------" << endl;
mp1.erase(1);
mp1.erase(54);
mp1.print();
cout << endl << "--------------------------------------" << endl;
Brant::unordered_set<int> st1;
st1.insert(1);
st1.insert(54);
st1.insert(2);
st1.insert(3);
st1.insert(4);
st1.insert(6);
st1.insert(6);
st1.print();
cout << "Erase:---------------" << endl;
st1.erase(1);
st1.erase(54);
st1.print();
}迭代器测试:
void test_iterator01()
{
Brant::unordered_map<string, string> dict;
dict.insert({ "sort","排序" });
dict.insert({ "left","左边" });
dict.insert({ "right","右边" });
dict.insert({ "string","字符串" });
Brant::unordered_map<string, string>::iterator it = dict.begin();
while (it != dict.end())
{
cout << it->first << " : " << it->second << endl;
++it;
}
cout << endl;
}
void test_iterator02()
{
Brant::unordered_map<string, int> countMap;
string arr[] = { "苹果","西瓜","菠萝","草莓","菠萝","草莓" ,"菠萝","草莓"
, "西瓜", "菠萝", "草莓", "西瓜", "菠萝", "草莓","苹果" };
for (auto e : arr)
{
countMap[e]++;
}
for (auto kv : countMap)
{
cout << kv.first << " " << kv.second << endl;
}
}





![[论文翻译] GIKT: A Graph-based Interaction Model forKnowledge Tracing](https://img-blog.csdnimg.cn/img_convert/88e82382843ebc7b2de32687e29bd416.png)