个人主页: 深情秋刀鱼@-CSDN博客
数据结构专栏:数据结构与算法
源码获取:数据结构: 上传我写的关于数据结构的代码 (gitee.com)

目录
一、堆
1.堆的概念
2.堆的定义
二、堆的实现
1.初始化和销毁
2.插入
向上调整算法
3.删除
向下调整算法
4.取堆顶元素
5.判空
三、Top_k问题
1.问题描述
2.面试中的Top_k问题
四、堆排序
1.建堆
2.堆排序
五、堆的时间复杂度
1.建堆
a.树中高度与节点的关系
b.向下调整建堆算法
c.向上调整建堆算法
2.堆排序
一、堆
1.堆的概念
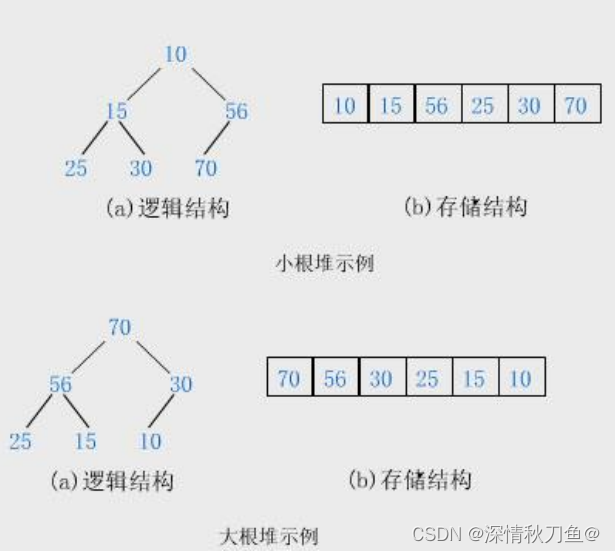
堆是一棵完全二叉树,且其中的节点总是不大于(或不小于某个值)。如果堆中的节点总是不大于某个值(根节点最大),称为大根堆;如果堆中的节点总是不小于某个值(根节点最小)将根节点最小的堆称为小根堆。
大根堆和小根堆描述的是双亲节点和子节点之间的关系,而子节点之间没有直接的联系。
2.堆的定义
typedef int HPDataType; //堆 typedef struct Heap { HPDataType* a; int size; int capacity; }Heap;二叉树一般可以使用两种结构存储,一种顺序结构(数组),一种链式结构(链表)。由于堆是一棵完全二叉树,用数组结构存储较为简洁。
数组中双亲节点和子节点之间的关系:
- 当双亲结点的下标为i时,左子节点的下标=2 * i + 1,右子节点的下标=2 * i + 2
- 当子节点的下标为i时,双亲节点的下标=(i - 1)/ 2
二、堆的实现
1.初始化和销毁
//初始化 void HPInit(Heap* php) { assert(php); php->a = NULL; php->size = php->capacity = 0; } //销毁 void HPDestroy(Heap* php) { assert(php); free(php->a); php->a = NULL; php->size = php->capacity = 0; }
2.插入
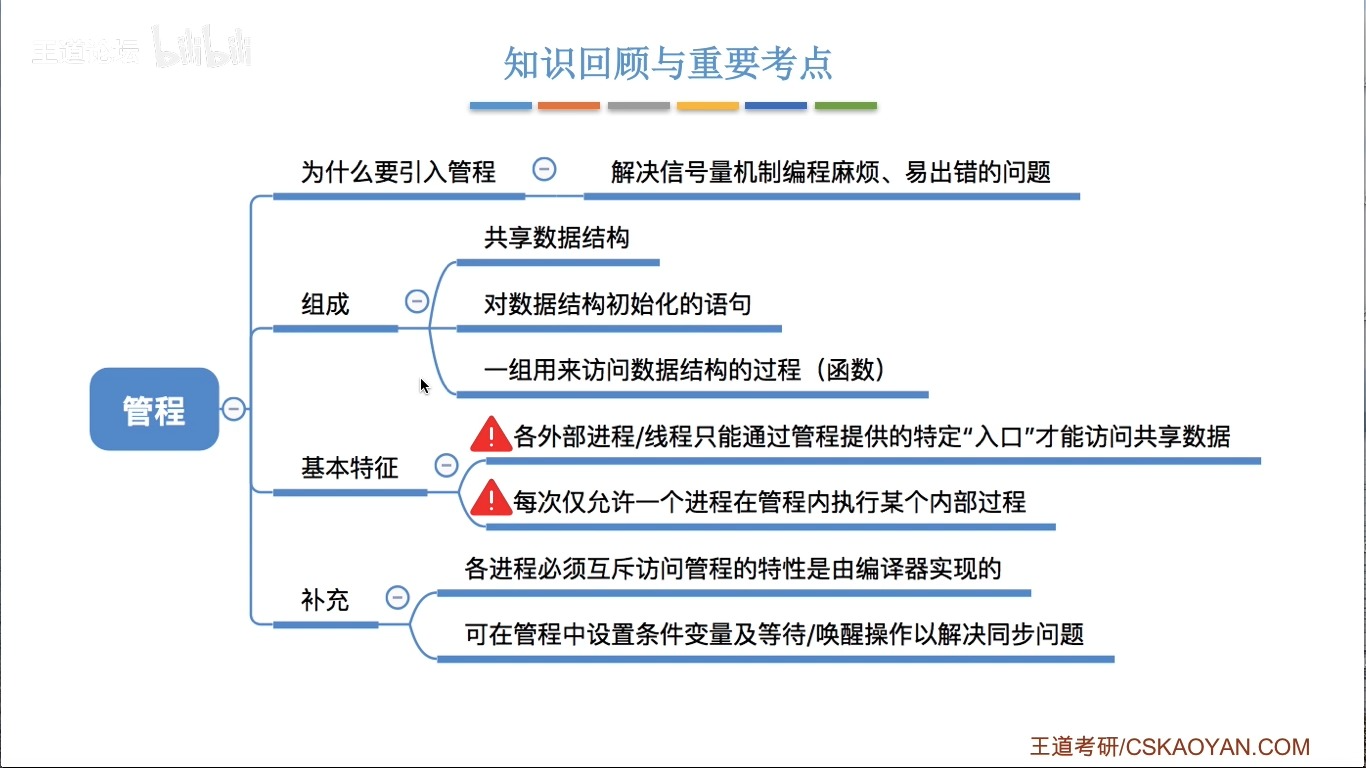
堆在内存中是以数组的形式存储的,在逻辑上需要将数组看成一棵完全二叉树。向堆中插入数据时要保证堆的结构不被破坏,并将其调整为小根堆或大根堆时需要用到向上调整算法。
向上调整算法
使用前提:左右子树必须是一个堆,才能调整。
算法实现:以小根堆为例,在数组尾部(下标为size-1)的位置插入数据(记下标为child),被插入数据child通过下标之间的关系找到child所在的这棵子树的根(记下标为parent)并与根节点比较,如果a[child]<a[parent]说明此时双亲节点大于子结点的,不符合小根堆的性质,此时需要交换child与parent的位置并更新child和parent的值,一直到堆顶(下标为0)则调整结束。
//交换 void Swap(HPDataType* a, HPDataType* b) { HPDataType tmp = *b; *b = *a; *a = tmp; } //向上调整算法(小根堆) void AdjustUP(HPDataType* a, int child) { int parent = (child - 1) / 2; while (child > 0) { if (a[parent] > a[child]) { Swap(&a[parent], &a[child]); child = parent; parent = (child - 1) / 2;//更新下标值 } else break; } }
- 图解(小根堆):

- 代码实现:
//插入
void HPPush(Heap* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));
if (tmp == NULL)
{
perror("realloc fail!");
return;
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size++] = x;
AdjustUP(php->a, php->size - 1);
}3.删除
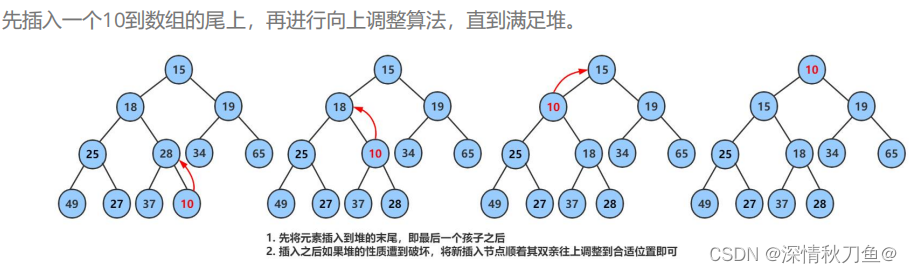
删除规定只删除堆顶元素(删除堆尾元素size--即可),删除堆顶元素的同时需要保持结构不变,需要用到向下调整算法。
向下调整算法
使用前提:左右子树必须是一个堆,才能调整。
算法实现:以小根堆为例,将首(B)尾(A)元素交换,在尾部删除堆顶元素B,在堆顶的尾元素A通过向下调整算法调整到合适的位置再形成堆。新的堆顶元素A下标为0(记为parent),以parent为根的两个子节点分别为左child节点(下标2*parent+1)、右child节点(下标2*parent+2),为满足小根堆的性质,我们需要在这两个节点中找到较小的一个与元素A交换成为新的根,元素A成为子节点后再向下寻找以元素A为根的两个子节点,一直到堆底调整结束。
//向下调整算法 void AdjustDown(HPDataType* a, int n, int parent) { //假设法 int child = 2 * parent + 1; while (child < n) { //两个子节点中较小的那个(注意边界的处理) if (child + 1 < n && a[child] > a[child + 1]) child++; if (a[parent] > a[child]) { Swap(&a[parent], &a[child]); parent = child; child = 2 * parent + 1; } else break; } }在判断两个子节点的大小时不妨先假设左子节点大,进入循环后再判断左右子节点的大小。
- 图解(小根堆):
- 代码实现:
//删除(删除堆顶的数据)
void HPPop(Heap* php)
{
assert(php && php->size > 0);
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
AdjustDown(php->a, php->size, 0);
}4.取堆顶元素
//取堆顶 HPDataType HPTop(Heap* php) { assert(php && php->size > 0); return php->a[0]; }
5.判空
//判空 bool HPEmpty(Heap* php) { assert(php); return php->size == 0; }
三、Top_k问题
1.问题描述
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。 比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
1. 用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
简单来说:以求取数组中前六个最大的元素为例,将一个元素个数为n的数组调整为大堆后,堆顶的元素就是数组中n个元素的最大值,获取堆顶元素后将堆顶元素删除(删除的步骤是堆顶元素先与堆尾元素交换,在堆尾删除堆顶元素),通过向下调整算法调整堆的结构使其仍然呈大堆排列,排列之后新的堆顶元素就是数组中n-1个元素中的最大值,依此类推。
- 代码实现:
int a[] = { 1,2,3,5,4,9 }; int k;//前k个 scanf_s("%d", &k); while (k--) { printf("%d ", HPTop(&hp)); HPPop(&hp); }
- 运行结果
2.面试中的Top_k问题
C语言:文件操作详解-CSDN博客
- 给出N个整数,存储在磁盘文件中,要求取出最大的前k个元素。
这个问题属于最常规的Top_k问题,建大堆然后依次popk个元素即可。但是面试中往往不会这么简单,这种方法固然存在一定的缺陷:当N过于大时,占用内存空间较多,如果给出10亿个整数就需要占用将近4G的内存空间,如果面试官对内存空间做出限制,显然这种方法就行不通了。
- 给出N个整数,存储在磁盘文件中,要求取出最大的前k个元素且占用的内存空间不允许超过1KB。
介绍一种很巧妙的方法:取前k个元素建小堆,然后用剩下的N-k个元素与堆顶元素比较,如果大于堆顶元素则直接覆盖堆顶元素,成为新的堆顶元素,最后用向下调整算法调整结构,依次遍历完所有的数据。这样留在堆中的元素就是最大的前k个元素。
//在text中创建N个数据 void CreateN() { int n; scanf("%d", &n); srand((unsigned int)time(0)); const char* FileName = "D:\\Git code\\data-structure\\Project_Heap\\Project_Heap\\data.txt";//文件地址 FILE* fin = fopen(FileName, "w"); if (fin == NULL) { perror("fopen fail"); return; } for (int i = 1; i <= n; i++) { int x = (rand() + i) % 10000000; fprintf(fin, "%d\n", x); } fclose(fin); } //Top_k void Test3() { CreateN(); const char* FileName = "D:\\Git code\\data-structure\\Project_Heap\\Project_Heap\\data.txt"; FILE* fout = fopen(FileName, "r"); int k; scanf("%d", &k); int* kMinHeap = (int*)malloc(sizeof(int) * k); if (kMinHeap == NULL) { perror("malloc fail"); return; } //将文件中的数据(前k个)读取到数组中 for (int i = 0; i < k; i++) { fscanf(fout, "%d", &kMinHeap[i]); } //建堆 for (int i = (k - 1 - 1) / 2; i >= 0; i--) { AdjustDown(kMinHeap, k, i); } int x; while (fscanf(fout, "%d", &x) > 0) { if (x > kMinHeap[0]) { kMinHeap[0] = x; AdjustDown(kMinHeap, k, 0); } } for (int i = 0; i < k; i++) { printf("%d\n", kMinHeap[i]); } fclose(fout); }
四、堆排序
1.建堆
给定一个数组,要求将其调整为大堆或小堆。我们可以将原数组直接看成一棵完全二叉树,然后利用向上或向下调整算法将其调整为大堆或小堆,大堆和小堆是可以自由切换的,只需要更改向下和向上调整算法中的比较逻辑即可。
- 向上调整算法建小堆
int a[] = { 2,3,1,4,6,5,9 }; Heap hp; HPInit(&hp); int n = sizeof(a)/xizeof(int); for (int i = 1; i < n; i++) AdjustUP(a, i);建堆逻辑:总是保证前i个数据具有堆的性质,当i=n时,整棵树都具有了堆的性质。
- 向下调整算法建小堆
int a[] = { 2,3,1,4,6,5,9 }; Heap hp; HPInit(&hp); int n = sizeof(a)/sizeof(int); for (int i = (n - 1 - 1) / 2; i < n; i++) AdjustDown(a, n, i);在向下调整算法建堆时,我们从倒数的第一个非叶子结点的子树开始调整,一直调整到根结点的树,就可以调整成堆。
建堆逻辑:总是保持后i个数据具有堆的性质,当i=0时,整棵树都具有了堆的性质。
- 图解(大根堆):
2.堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
1. 建堆
- 升序:建大堆
- 降序:建小堆
2. 利用堆删除思想来进行排序:建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && a[child] > a[child + 1])
child++;
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = 2 * parent + 1;
}
else
break;
}
}
//交换
void Swap(HPDataType* a, HPDataType* b)
{
HPDataType tmp = *b;
*b = *a;
*a = tmp;
}
//堆排序(O(N*logN))
void HPSort(HPDataType* a, int n)
{
//降序:建小堆
//升序:建大堆
//for (int i = 1; i < n; i++)
// AdjustUP(a, i);//向上调整建堆
for (int i = (n - 1 - 1) / 2; i < n; i++)
AdjustDown(a, n, i);
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}图解(升序大根堆):

五、堆的时间复杂度
1.建堆
a.树中高度与节点的关系
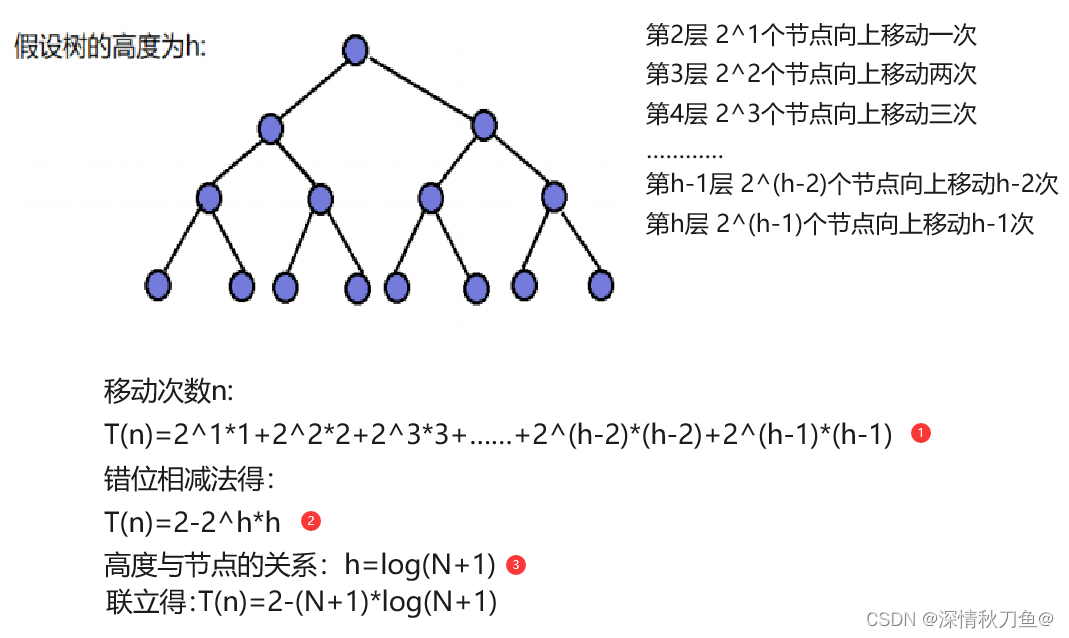
设有一棵高度为h的满二叉树,如下图:
根据递推公式我们可以得到节点N与高度h的关系:F(h)=2^0+2^1+2^2+.....+2^(h-1)。根据等比数列求和公式,F(h)=2^h-1。
一棵完全二叉树节点最多的情况是一棵满二叉树(最后一层全满),节点最少的情况是最后一层有且仅有一个节点的情况。
- 满二叉树:F(h)=2^h-1=N——h=log(N+1)
- 完全二叉树节点最少情况:F(h)=2^(h-1)=N——h=logN+1
综上完全二叉树的节点应在log(N+1)与logN+1之间,根据大O的渐进表示法为logN。
b.向下调整建堆算法
在向下调整建堆的过程中,我们选择从最后一个非叶子节点的节点开始调整,在计算时间复杂度时,只考虑最坏的情况,将堆简化看作一棵满二叉树,即每个双亲节点都需要调整到最底部,如第一层2^0个节点向下移动4次,第二层2^1个节点向下移动2层,第三层2^2个节点向下移动1次。
综上,向下调整建堆得时间复杂度为O(N)。
c.向上调整建堆算法
在向上调整建堆中,我们选择从第一个子节点开始调整。还是只考虑最坏的情况并将堆简化为一棵满二叉树。从第2个节点开始,每个节点都需要向上调整高度次,即第二层2^1个节点向上移动1次,第三层2^2个节点向上移动2次,第四层2^3个节点(看作满二叉树)向上移动3次。
综上,向下调整建堆得时间复杂度为O(N*logN)。
2.堆排序
建堆时间复杂度对比:
- 向上调整建堆:O(N*logN)
- 向下调整建堆:O(N)
堆排序的实现:
void HPSort(HPDataType* a, int n) { //降序:建小堆 //升序:建大堆 //for (int i = 1; i < n; i++) // AdjustUP(a, i);//向上调整建堆 for (int i = (n - 1 - 1) / 2; i < n; i++) AdjustDown(a, n, i); int end = n - 1; while (end > 0) { Swap(&a[0], &a[end]); AdjustDown(a, end, 0); --end; } }建堆结束后,类比调整算法的推导可以得出排序的时间复杂度是O(N*logN)。