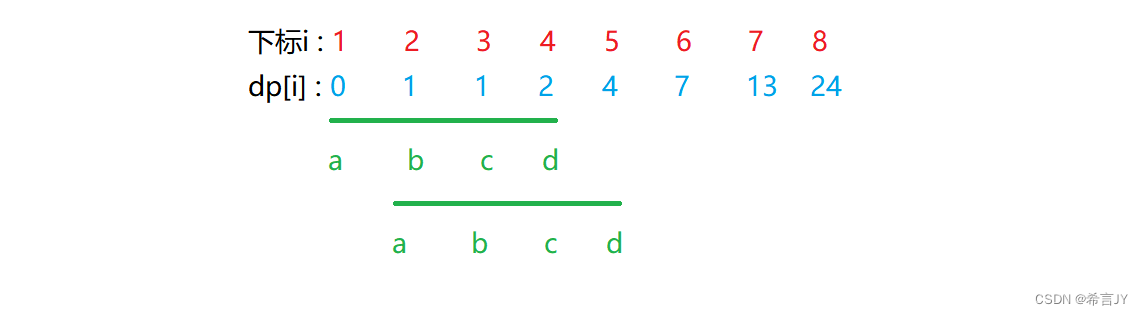
实时阴影是电子游戏中最为重要的画面效果之一。在计算机图形学中,通常使用阴影映射方法来实现实时阴影。
游戏开发部正在开发一款 2D 游戏,同时希望能够在 2D 游戏中模仿 3D 游戏的光影效果,请帮帮游戏开发部!
给定 x-y 平面上的 n 个矩形,矩形的边界平行于坐标轴,且可能相互重叠。同时给定点光源的坐标。现有 m 次操作,每次操作添加或删除一个矩形,或询问 x 轴上的一点是否在阴影内。
输入格式
第一行,两个整数
n
,
m
n,m
n,m(
1
≤
n
,
m
≤
2
×
1
0
5
1≤n,m≤2×10^5
1≤n,m≤2×105)。
第二行,两个整数
l
x
,
l
y
l_x,l_y
lx,ly,表示光源的坐标为
(
l
x
,
l
y
)
(l_x,l_y)
(lx,ly)。
∣
l
x
∣
≤
2
×
1
0
5
,
0
<
l
y
≤
2
×
1
0
5
|l_x|≤2×10^5,0<l_y≤2×10^5
∣lx∣≤2×105,0<ly≤2×105。
接下来
n
n
n 行,每行 5 个整数
i
d
,
x
,
y
,
w
,
h
id,x,y,w,ℎ
id,x,y,w,h,表示编号为
i
d
id
id 的矩形,左下角坐标为
(
x
,
y
)
(x,y)
(x,y),宽为
w
w
w,高为
h
ℎ
h。
接下来
m
m
m 行,每行先输入一个正整数
o
p
t
opt
opt∈[1,3]。
- 若 o p t = 1 opt=1 opt=1,则接下来输入 5 个整数 i d , x , y , w , h id,x,y,w,ℎ id,x,y,w,h,表示增加一个编号为 i d id id,且左下角坐标为 ( x , y ) (x,y) (x,y),宽和高为 w w w 和 h ℎ h 的矩形。
- 若 o p t = 2 opt=2 opt=2,则接下来输入一个整数 i d id id,表示删除编号为 i d id id 的矩形。
- 若 o p t = 3 opt=3 opt=3,则接下来输入一个整数 p p p,表示查询坐标 ( p , 0 ) (p,0) (p,0) 是否在阴影中。
1
≤
i
d
≤
4
×
1
0
5
1≤id≤4×10^5
1≤id≤4×105
∣
x
∣
≤
2
×
1
0
5
,
0
<
y
≤
2
×
1
0
5
|x|≤2×10^5,0<y≤2×10^5
∣x∣≤2×105,0<y≤2×105
0
<
w
,
h
≤
2
×
1
0
5
0<w,ℎ≤2×10^5
0<w,h≤2×105
∣
p
∣
≤
1
0
9
|p|≤10^9
∣p∣≤109
保证任意时刻场景中所有矩形的
i
d
id
id 互不相同。保证所有矩形各个顶点的
y
y
y 坐标一定严格小于光源的
y
y
y坐标。若询问点在阴影的边界上,仍算作在阴影内。
输出格式
对于每个
o
p
t
=
3
opt=3
opt=3 的询问,若询问的点在阴影中,则输出一行 YES,否则输出一行 NO。
样例
input
3 19
4 7
1 1 1 2 1
2 6 1 2 3
3 5 2 4 1
3 -1
3 0
3 2
3 3
3 4
3 5
3 6
3 12
3 13
3 14
1 4 4 5 2 1
3 3
3 4
3 5
3 18
3 19
2 1
3 2
3 3
output
NO
YES
YES
NO
NO
NO
YES
YES
YES
NO
NO
YES
YES
YES
NO
NO
NO
提示
在进行所有修改操作之前,所有矩形的位置如下 (绿色部分为阴影区域):

在加入一个矩形后,所有矩形的位置如下:

在删除一个矩形后,所有矩形的位置如下:

很容易想到利用线段树维护阴影区间,添加阴影即为在[l,r]范围内进行+1操作,删除阴影为-1
但是本题的数据范围过大,特别注意当光源与矩形非常接近时,光线几乎平行于x轴,这时用long long都会存在爆精度问题
所以必须进行离散化
我们可以发现需要用到的坐标是有限的,最多不超过 2 × n + m 2×n+m 2×n+m个坐标点,用到的坐标点为线段端点(l,r)和查询位置p
AC代码如下
注意这题的时间复杂度卡的很死,需要采用IO加速,同时切忌使用STL容器
#include <iostream>
#include <algorithm>
#include <map>
#include <cmath>
using namespace std;
#define int long long
const int max_n = 5e5 + 50;
const int max_m = 5e5 + 50;
const int max_len = 1e6 + 50;
const double eps = 1e-8;
typedef struct {
int idx, x1, y1, x2, y2;
}node;
typedef struct {
int opt[6];
}query;
typedef struct {
double first, second;
}line;
int n, m;
node arr[max_n];
query qarr[max_m];
int tmpidx, lineidx;
double tmparr[max_len];
line lines[max_n + max_m];
map<double, int>dict;
int tree[max_len];
inline int read() {
int x = 0, y = 1; char c = getchar();
while (c < '0' || c > '9') {
if (c == '-') y = -1;
c = getchar();
}
while (c >= '0' && c <= '9') {
x = x * 10 + c - '0';
c = getchar();
}
return x * y;
}
inline int lowbit(int x) {
return x & -x;
}
int ask(int p) {
int res = 0;
for (int i = p; i > 0; i -= lowbit(i)) {
res += tree[i];
}
return res;
}
void add(int p, int x) {
for (int i = p; i < max_len; i += lowbit(i)) {
tree[i] += x;
}
}
double project(int x, int y) {
if (x == arr[0].x1) return x;
double k = double(y - arr[0].y1) / double(x - arr[0].x1);
double b = k * x - y;
return b / k;
}
void process(node n) {
double l, r, ret;
l = r = project(n.x1, n.y1);
ret = project(n.x1, n.y2);
l = min(l, ret); r = max(r, ret);
ret = project(n.x2, n.y1);
l = min(l, ret); r = max(r, ret);
ret = project(n.x2, n.y2);
l = min(l, ret); r = max(r, ret);
tmparr[tmpidx++] = l;
tmparr[tmpidx++] = r;
lines[lineidx++] = line{ l,r };
}
inline bool equal(double x, double y) {
return fabs(x - y) < eps;
}
void discrete() {
sort(tmparr, tmparr + tmpidx);
int cnt = 0;
for (int i = 0; i < tmpidx; i++) {
if (i == 0) {
dict[tmparr[i]] = ++cnt;
continue;
}
if (tmparr[i] != tmparr[i - 1])
dict[tmparr[i]] = ++cnt;
}
}
signed main() {
n = read(); m = read();
arr[0].x1 = read();
arr[0].y1 = read();
int tmpid;
int cnt;
tmpidx = lineidx = 0;
for (cnt = 1; cnt <= n; cnt++) {
tmpid = read();
arr[tmpid].x1 = read();
arr[tmpid].y1 = read();
arr[tmpid].x2 = arr[tmpid].x1 + read();
arr[tmpid].y2 = arr[tmpid].y1 + read();
arr[tmpid].idx = cnt - 1;
process(arr[tmpid]);
}
int optnum;
for (int i = 1; i <= m; i++) {
qarr[i].opt[0] = read();
switch (qarr[i].opt[0])
{
case 1:
tmpid = read();
arr[tmpid].x1 = read();
arr[tmpid].y1 = read();
arr[tmpid].x2 = arr[tmpid].x1 + read();
arr[tmpid].y2 = arr[tmpid].y1 + read();
arr[tmpid].idx = cnt++ - 1;
process(arr[tmpid]);
qarr[i].opt[1] = tmpid;
break;
case 2:
qarr[i].opt[1] = read();
break;
case 3:
qarr[i].opt[1] = read();
tmparr[tmpidx++] = qarr[i].opt[1];
break;
default:
break;
}
}
discrete();
for (int i = 0; i < n; i++) {
double l = lines[i].first;
double r = lines[i].second;
l = dict[l]; r = dict[r];
add(l, 1);
add(r + 1, -1);
}
for (int i = 1; i <= m; i++) {
if (qarr[i].opt[0] == 1) {
int p = qarr[i].opt[1];
p = arr[p].idx;
double l = lines[p].first;
double r = lines[p].second;
l = dict[l]; r = dict[r];
add(l, 1);
add(r + 1, -1);
}
else if (qarr[i].opt[0] == 2) {
int p = qarr[i].opt[1];
p = arr[p].idx;
double l = lines[p].first;
double r = lines[p].second;
add(dict[l], -1);
add(dict[r] + 1, 1);
}
else {
double p = qarr[i].opt[1];
if (ask(dict[p])) {
printf("YES\n");
}
else printf("NO\n");
}
}
return 0;
}