路径规划算法中有两种算法使用最普遍，第一个是Dijkstr算法，第二个是A*算法，两个算法各有千秋，Dijkstra算法可以保证最优解，但是复杂度较高，尤其当点数量较多时，A*算法是一种启发式搜索算法，它不保证最优解，但成本很低，也是很多机器人移动或者游戏中人物自动寻路场景中常用的算法。
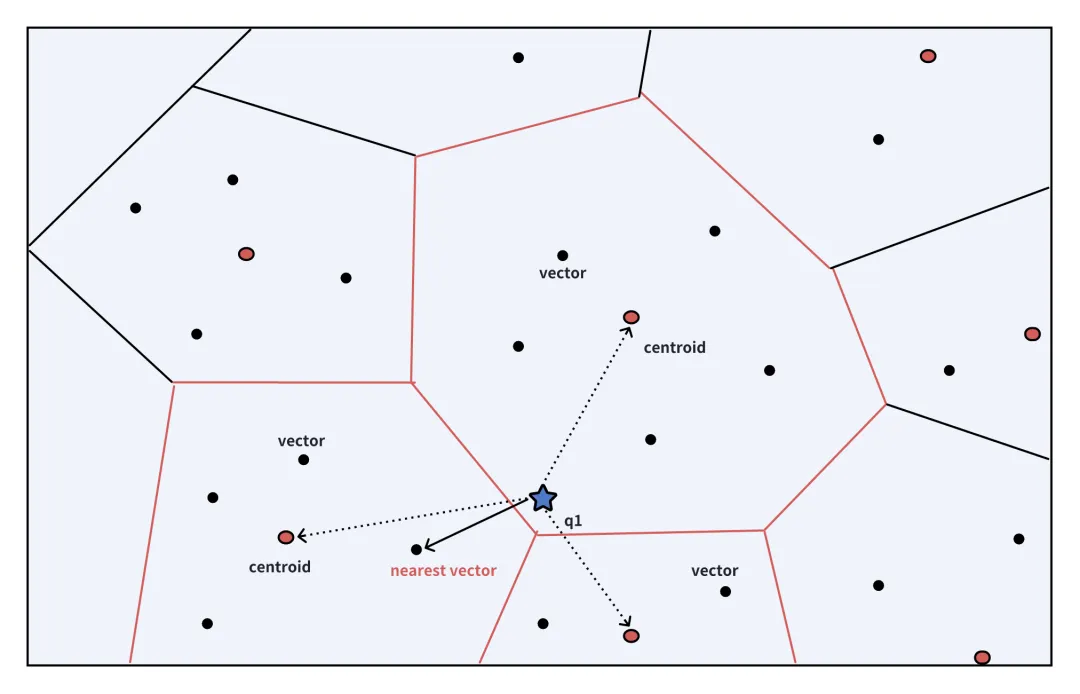
下面来说下大概得逻辑，假设有30*30的方格，从1,1点要到25,20点，会先从1,1出发，查询1,1能到达的点，假设1,1能够到达（0,1),(1,0),(1,2),(2,1)这四个点，那么求出四个点中哪个点距离目标点(25,20)的曼哈顿距离最近，得到这个这里距离最近的点之后，再找出这个点能够到达的点，从它能够到达的点中再求出四个点中哪个点距离目标点(25,20)的曼哈顿距离最近。依此类推，直到到达目标点。
ps:曼哈顿距离也就是横向距离加上纵向距离，而不是勾股定理求出的横向距离的平方和纵向距离的平方再开根，因为一般使用A*算法的更多的是街道或者网格状的场景，用曼哈顿距离更加符合实际场景。
下面可以通过threejs来演示，首先在threejs场景中绘制一个30*30的网格，在绘制网格的时候就正好存储每个网格的点，并用x.y为点的名字，再存储每个点能到达点的路线，另外为了演示更真实可以防止一些障碍物，并在绘制场景的时候去掉能连接到障碍物的路线，
initTable() {
const cylinderMaterial = new THREE.MeshLambertMaterial({ color: '#d3d3d3' })
const table = []
for (let i = 0; i < 30; i++) {
for (let j = 0; j < 30; j++) {
const boxGeometry = new THREE.BoxGeometry(9, 9, 9)
const box1 = new THREE.Mesh(boxGeometry, cylinderMaterial)
box1.position.set(i * 10, j * 10, 5)
// this.scene.add(box1)
box1.updateMatrix()// 更新模型变换矩阵
const boxMesh = box1.geometry.applyMatrix4(box1.matrix)// 启动并应用变换矩阵
table.push(boxMesh)
const params = { name: i + '.' + j, x: (i * 10), y: (j * 10) }
this.pointList.push(params)
if (i > 1) {
this.roadList.push({ begin: i + '.' + j, end: (i - 1) + '.' + j })
}
if (j > 1) {
this.roadList.push({ begin: i + '.' + j, end: i + '.' + (j - 1) })
}
this.roadList.push({ begin: i + '.' + j, end: (i + 1) + '.' + j })
this.roadList.push({ begin: i + '.' + j, end: i + '.' + (j + 1) })
}
}
const bayGeometry = mergeGeometries(table)// 合并模型数组
const boxList = new THREE.Mesh(bayGeometry, cylinderMaterial)// 生成一整个新的模型
this.scene.add(boxList)
for (let i = 0; i < this.roadList.length; i++) {
for (let j = 0; j < this.obstacle.length; j++) {
if (this.roadList[i].begin === (this.obstacle[j].x + '.' + this.obstacle[j].y) ||
this.roadList[i].end === (this.obstacle[j].x + '.' + this.obstacle[j].y)) {
console.log(this.obstacle[j].x + '.' + this.obstacle[j].y)
this.roadList.splice(i, 1)
j--
}
}
}
},
这样一个网格布局就绘制完成，然后可以开始按照刚才的步骤实现具体的寻路过程，在寻路时每次获取到的点都存放到集合中，并用绘制方格的方法绘制路线方格，与网格用不同的颜色来区分。
buildPath() {
let begin = (parseInt(this.beginPoint.x) - 1) + '.' + (parseInt(this.beginPoint.y) - 1)
const end = (parseInt(this.endPoint.x) - 1) + '.' + (parseInt(this.endPoint.y) - 1)
this.removeOnce()
this.drawPoint(begin)
while (begin !== end) {
const result = this.calcDistance(begin, end)
this.drawPoint(result.point)
begin = result.point
}
},
calcDistance(begin, end) {
const tempRoads = []
for (let i = 0; i < this.roadList.length; i++) {
if (this.roadList[i].begin === begin) {
tempRoads.push(this.roadList[i].end)
}
}
let result = { distance: Infinity, point: '' }
for (let i = 0; i < tempRoads.length; i++) {
const beginX = tempRoads[i].split('.')[0]
const beginY = tempRoads[i].split('.')[1]
const endX = end.split('.')[0]
const endY = end.split('.')[1]
const distance = Math.abs(parseInt(endX - beginX)) + Math.abs(parseInt(endY - beginY))
if (distance < result.distance) {
result = { distance: distance, point: tempRoads[i] }
}
}
return result
},
drawPoint(point) {
const pointX = point.split('.')[0]
const pointY = point.split('.')[1]
const boxGeometry = new THREE.BoxGeometry(10, 10, 10)
const material = new THREE.MeshPhongMaterial({
color: '#00FF00', // 设置颜色
shininess: 20 // 设置高光大小，范围为0到128，默认值为30
})
const pointMesh = new THREE.Mesh(boxGeometry, material, 0)
pointMesh.position.set(parseInt(pointX) * 10, parseInt(pointY) * 10, 6)
pointMesh.name = 'path'
this.scene.add(pointMesh)
},我们可以先设置默认的起点和结束点看下效果，设置起始点为(1,1),结束点为(20.16),规划后看下效果：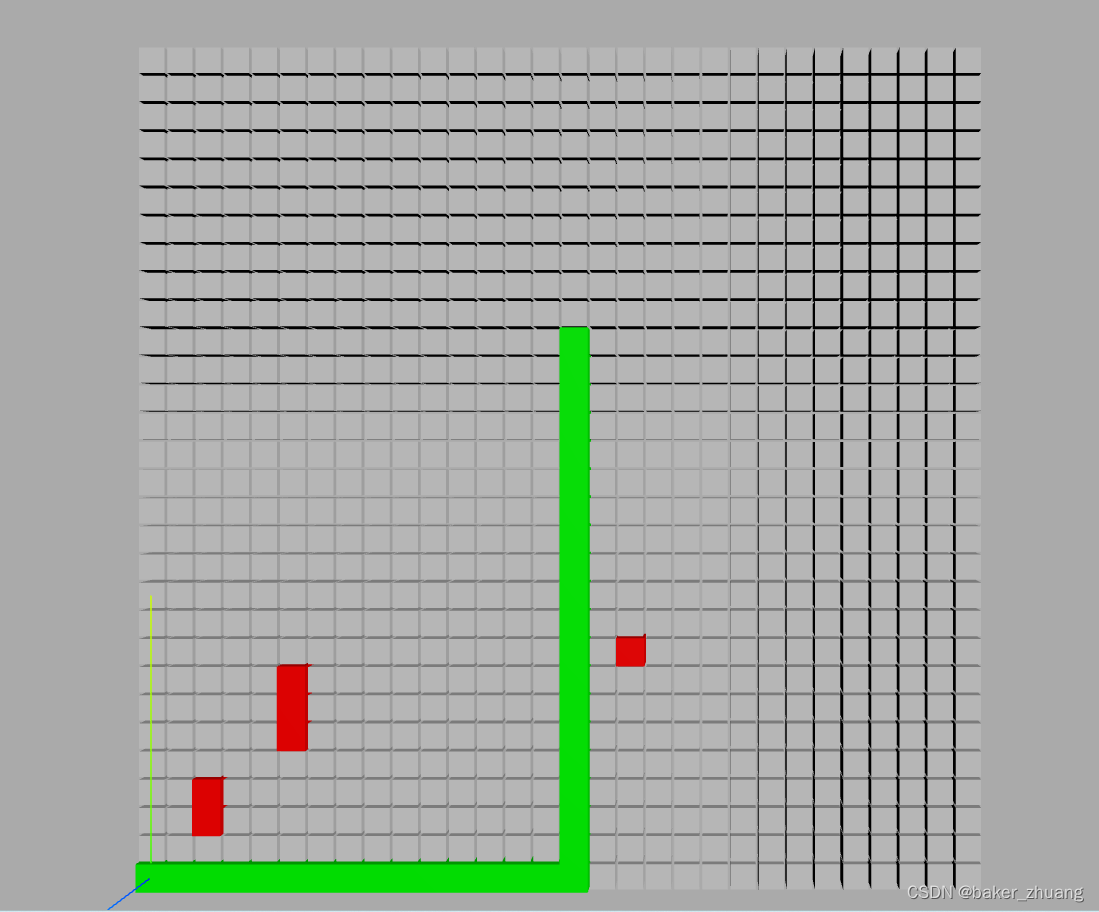
可以同样用上个章节的加入element的输入框来实现动态规划，并在每次规划后清除上一次规划的路线。
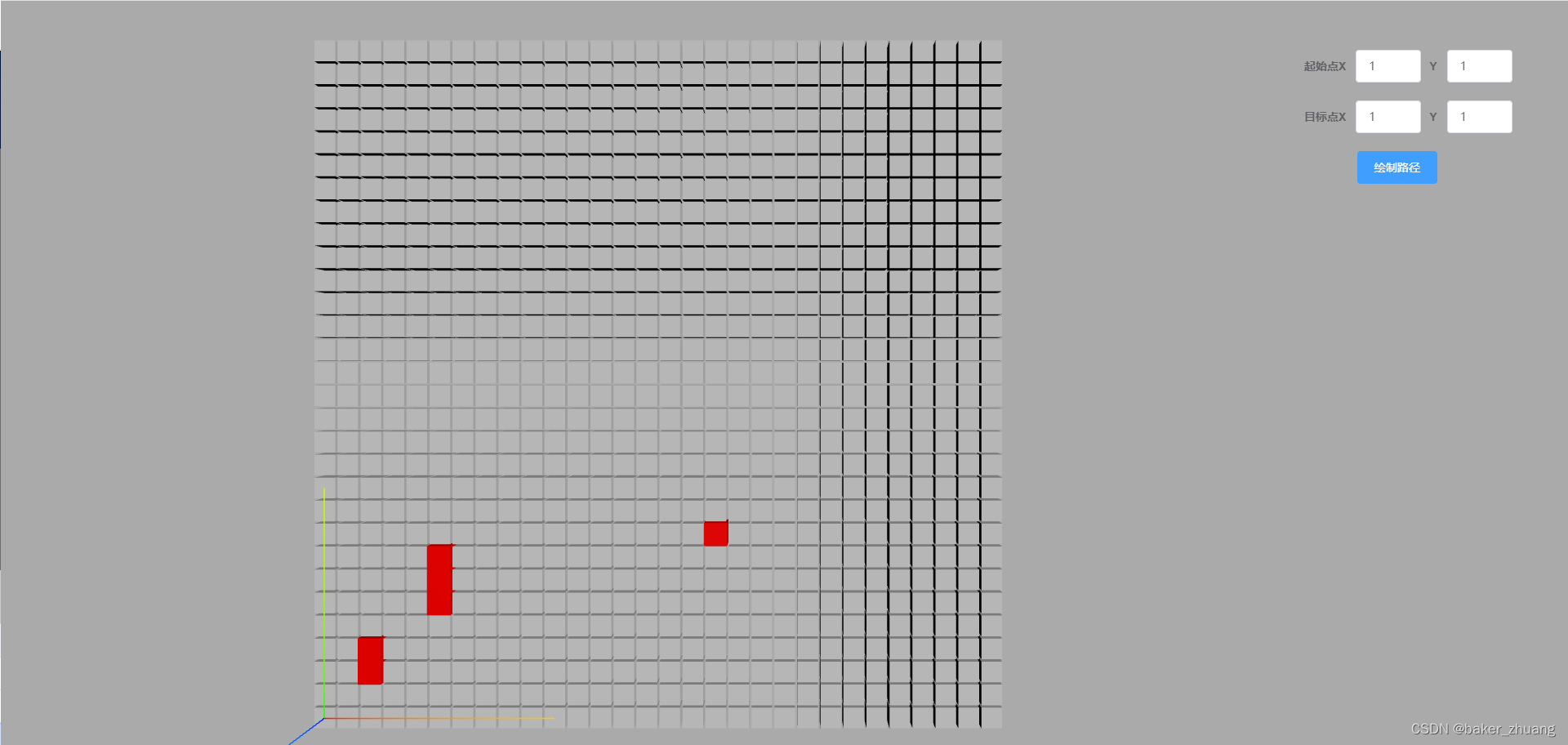
我们可以规划试试，效果如下，
A*初級
还可以把距离比较换成两个点之间的直线距离，效果如下：因为两个数相加的和相等的情况下，两个数越接近，直线距离最短，简单的说，周长相等的情况下，正方形的对角线最短。但是在实际地图中，转弯是需要花费成本的，所以还是使用曼哈顿距离更合适。
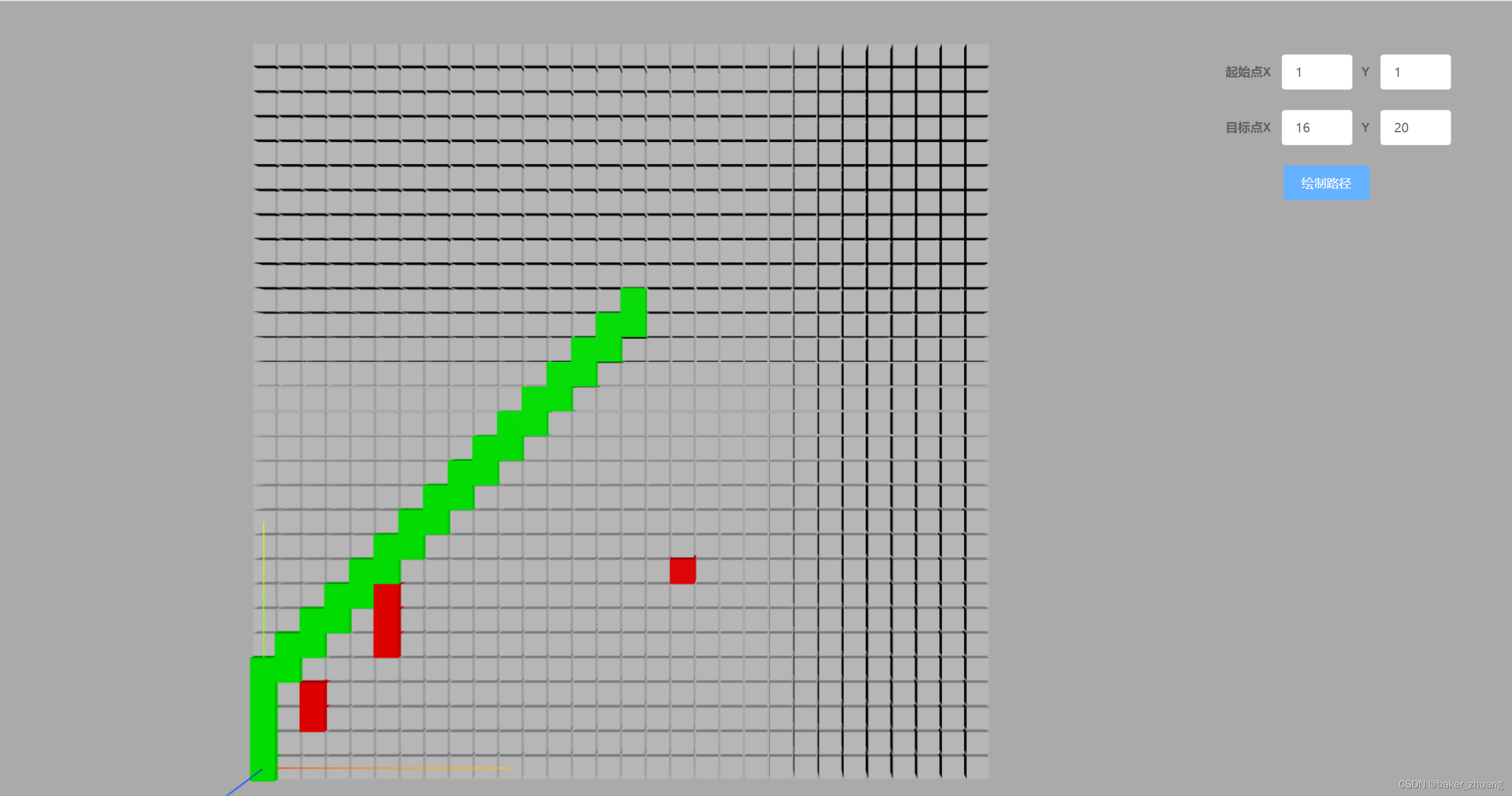不过此方式不太适合有障碍物的情况，因为在有复杂障碍物时，并不是距离越接近目标点花费成本越低，直到到达目标点，下面的章节再探讨复杂障碍物的处理方式。
