目录
快速排序
堆排序
桶排序
归并排序
拓扑排序
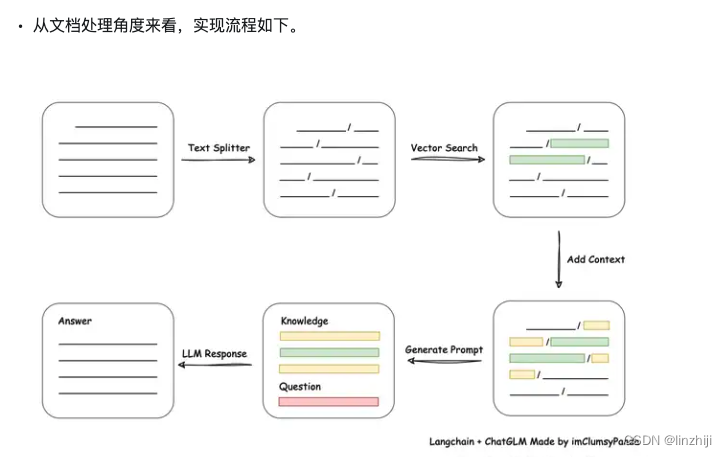
本文主要介绍那些我在刷题过程中常用到的排序算法: 快速排序,堆排序,桶排序,归并排序,拓扑排序
其余算法例如冒泡,插入这种效率特别低的算法就不介绍了,用的可能性极小
每一个算法都将采用例题加解释的方式进行介绍
快速排序
所谓快速排序,简单说就是枚举出一个中心点x,用双指针找出左边第一个大于等于x的元素i和右边第一个小于等于x的元素j,交换这两个元素,使得i左边维护的都是小于等于x的元素,j右边都是大于等于x的元素,再缩小范围继续排序
有点抽象是不是,那我们看一下快排的模板
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
可以看出排序操作是通过swap完成的,找到不符合要求的元素后交换他们的位置,使得i左边的元素都是小于x的,而j右边的元素都是大于x的,这样我们就可以把小于x和大于x的元素分开,但是分开后元素依旧是无序的,因此我们需要递归,缩小范围直到区间内只有一个元素
而递归的边界即可以用j表示也可以用i表示,当用i表示时递归函数如下
quick_sort(q,l,i-1),quick_sort(q,i,r);那什么时候用i什么时候用j呢,这就涉及到我们的边界问题
关于边界问题我这里引用别人的文章,里面已经说的很详细了:AcWing 785. 快速排序 - AcWing
如果不想了解这么多直接背模板就可以了,模板是可以直接套的
acwing 785.快速排序
给定你一个长度为n的整数数列。
请你使用快速排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
数据范围:
1 ≤ n ≤ 100000
参考代码:
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int n;
int q[N];
void quick_sort(int q[], int l, int r)
{
if (l>=r) return;
int x = q[(l+r)/2], i = l - 1, j = r + 1;
while(i<j)
{
do i++; while(q[i]<x);
do j--; while(q[j]>x);
if (i<j) swap(q[i],q[j]);
}
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
int main()
{
scanf("%d",&n);
for (int i=0;i<n;i++)
scanf("%d",&q[i]);
quick_sort(q,0,n-1);
for (int i=0;i<n;i++)
printf("%d ",q[i]);
return 0;
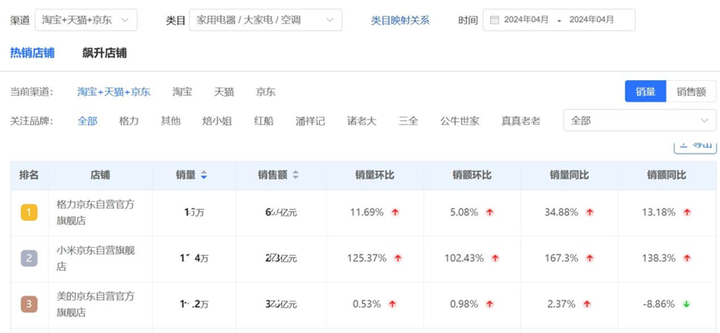
}堆排序
堆排序一般是通过priority_queue这个数据结构来实现的,通过优先队列实现大顶堆和小顶堆,用起来是极其方便的,而且排序效率高,时间复杂度为nlogn,唯一的缺点就是不好获取队列中间的元素
priority_queue<int,vector<int>,less<int>>q;//小顶堆
priority_queue<int,vector<int>,greater<int>>q;//大顶堆,不填第三个参数默认是大顶堆
优先队列的第三个参数是比较器,我们可以传入我们自定义的比较函数,也可以使用内置的表达方式如less<int>,表示整数越小的优先级越高
leetcode 347.前 K 个高频元素
347. 前 K 个高频元素 - 力扣(LeetCode)
给你一个整数数组
nums和一个整数k,请你返回其中出现频率前k高的元素。你可以按 任意顺序 返回答案。
利用优先队列维护一个大小为k的小顶堆即可,参考代码如下:
class Solution {
public:
static bool cmp(pair<int,int>&n,pair<int,int>&m)
{
return n.second>m.second;
}
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int,int>umap;
for(auto &p:nums)
{
umap[p]++;
}
priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(&cmp)>q(cmp);
for(auto &a:umap)
{
q.push(a);
if(q.size()>k)q.pop();
}
vector<int>ans;
while(!q.empty())
{
ans.emplace_back(q.top().first);
q.pop();
}
return ans;
}
};
关于优先队列的比较器,我在我的题解中有详细介绍:. - 力扣(LeetCode)
简单来说就是如果是内置数据类型可以使用内置的比较函数(如less,greater),如果是自定义类型则需要自定义比较函数,传入自定义函数有两种方式:1.将比较函数写在结构体中 2.用decltype获取函数类型
有兴趣的同学可以做一下 leetcode 295. 数据流的中位数 这题,考察的是大小顶堆的使用
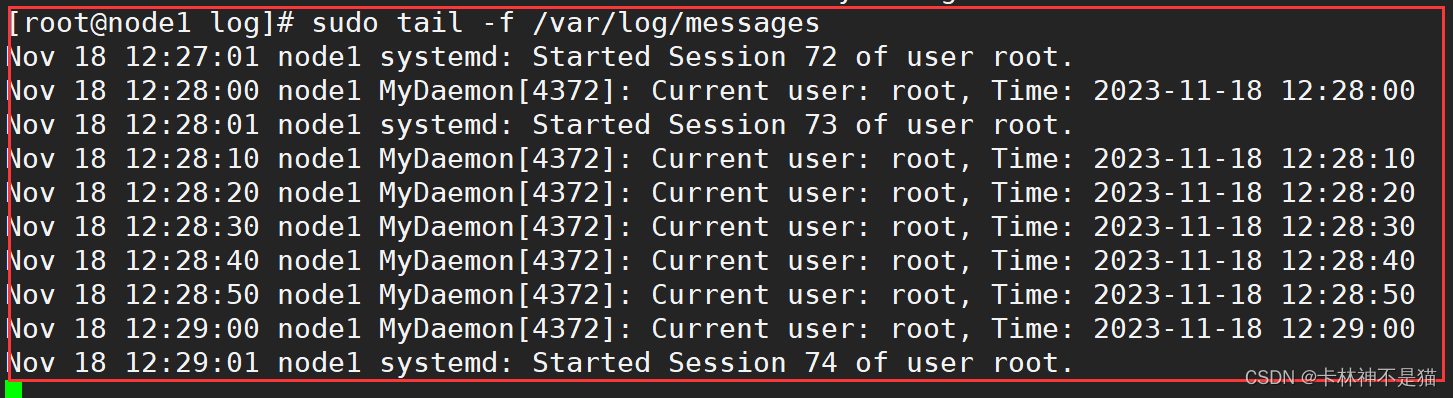
桶排序
桶排序有点类似于我们的哈希表,原理就是将元素一一映射到数组的一个位置上,每一个元素的映射规则都相同,映射结果唯一
f(x1)=y1 f(x2)=y2
有且仅有x1==x2时才有y1==y2
桶排序的映射函数并不复杂,往往是在原索引的基础上加上一个偏移量,在数组中完成映射
例如0<=nums[i]<100
那么我们就可以通过nums[i]的大小确定映射到哪个桶,因为nums[i]<100,所以我们用大于等于100的数去偏移就不会产生冲突
nums[i]->bucket[nums[i]+100]leetcode 215. 数组中的第K个最大元素数组中的第K个最大元素
215. 数组中的第K个最大元素 - 力扣(LeetCode)
给定整数数组
nums和整数k,请返回数组中第k个最大的元素。请注意,你需要找的是数组排序后的第
k个最大的元素,而不是第k个不同的元素。你必须设计并实现时间复杂度为
O(n)的算法解决此问题。
其中 -104 <= nums[i] <= 104
看到这个数据范围,我们可以发现这题可以使用桶排序,将nums[i]的值作为索引再加一个偏移量即可
参考代码:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
vector<int>bucket(21001,0);
for(int i=0;i<nums.size();i++){
bucket[nums[i]+10000]++;
}
int cnt=0;
for(int i=21000;i>=0;i--)
{
cnt+=bucket[i];
if(cnt>=k)
{
return i-10000;
}
}
return -1;
}
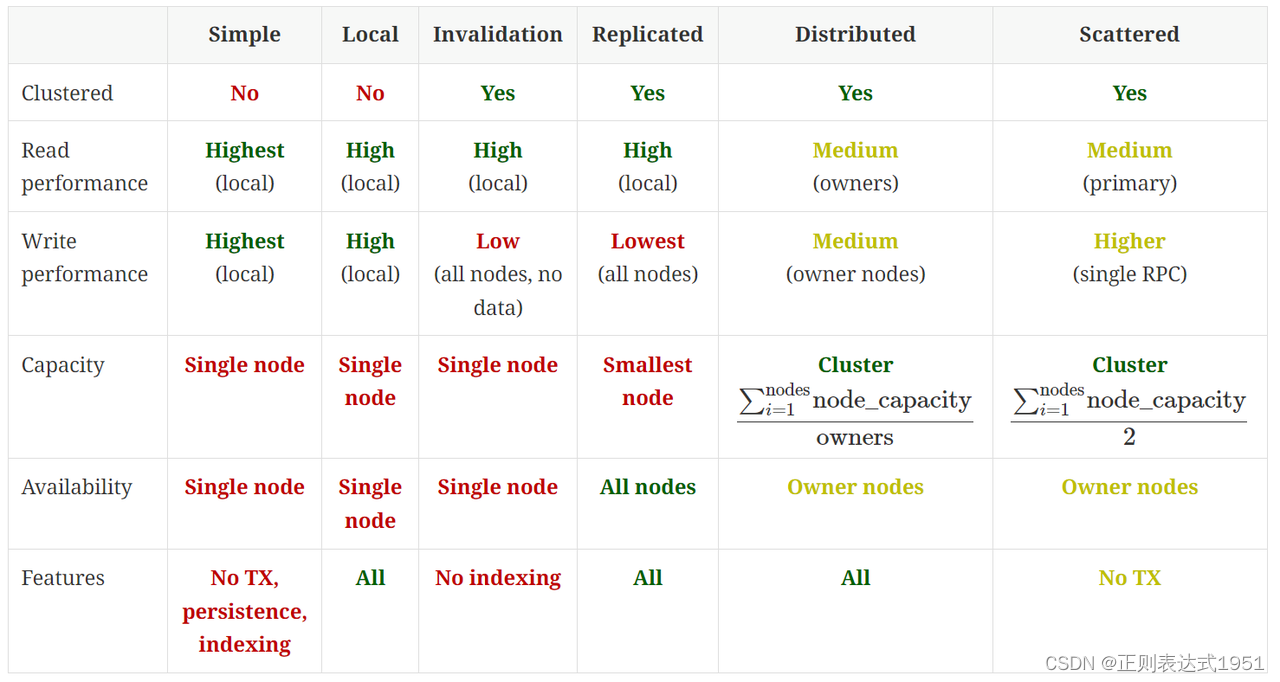
};归并排序
归并排序和快速排序的思想有点类似,都是用递归实现,只不过归并注重的是归,快排注重的是递
先看模板
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else tmp[k ++ ] = q[j ++ ];
while (i <= mid) tmp[k ++ ] = q[i ++ ];
while (j <= r) tmp[k ++ ] = q[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}
思路非常简单:就是将数组分为两部分,分别对两部分进行有序化处理,有序化之后通过两两比较将两个数组合并成一个数组,再将其赋值给原数组
leetcode 148.排序链表
148. 排序链表 - 力扣(LeetCode)
给你链表的头结点
head,请将其按 升序 排列并返回 排序后的链表
如果要求原地排序的话其实这题并不好想,当排序用在链表这种结构上时,逻辑要求会更高,但是总体思路是不变的:一分为二,分别有序化,最后再两两比较合并链表
参考代码:
class Solution {
private:
ListNode* merge(ListNode*l1,ListNode*l2)
{
ListNode*dummy=new ListNode(0);//虚拟节点
ListNode*ans=dummy;
while(l1&&l2)
{//排序
auto &node=l1->val<l2->val?l1:l2;
dummy->next=node;
dummy=dummy->next;
node=node->next;
}//多余的接到后面
if(l1)dummy->next=l1;
else dummy->next=l2;
return ans->next;
}
public:
ListNode* sortList(ListNode* head,ListNode*tail=nullptr) {
if(head==nullptr)return head;
if(head->next==tail)//只剩两个节点时
{
head->next=nullptr;
return head;
}
ListNode*fast=head;
ListNode*slow=head;
while(fast!=tail&&fast->next!=tail)
{
slow=slow->next;
fast=fast->next->next;
}
ListNode*mid=slow;//找到中间节点,将链表分成两份
return merge(sortList(head,mid),sortList(mid,tail));
}
};
拓扑排序
拓扑排序:对有向无环图(DAG)中的所有顶点进行线性排序,使得对于任意一对顶点u和v,如果图中存在一条从u指向v的有向边,那么在拓扑序列中u出现在v之前
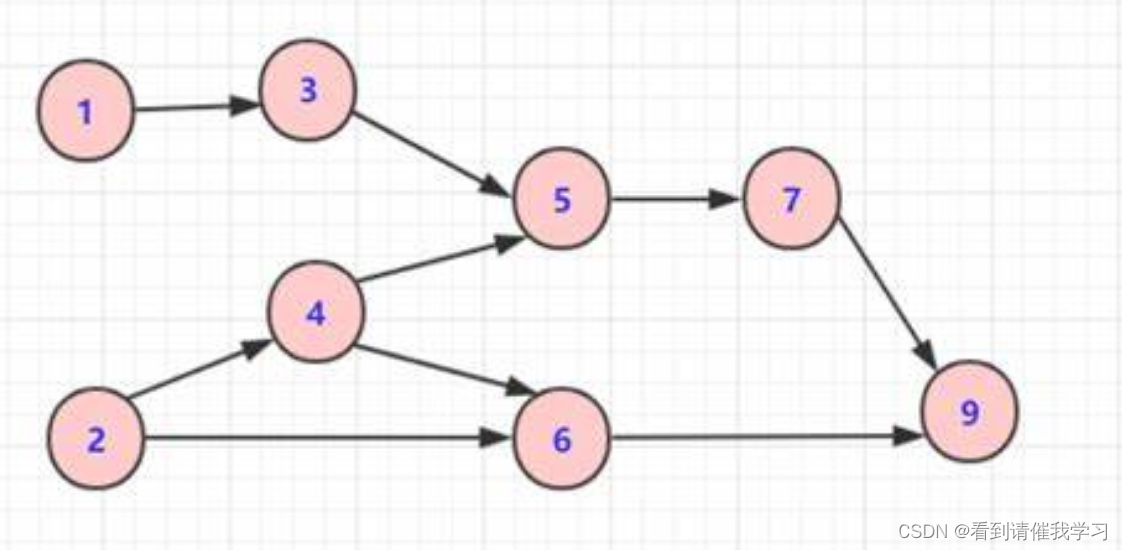
一句话说就是只有入度为0的点才能被选择,通过删除边(减少入度)实现节点的排序
最经典的拓扑排序就是先修课问题
leetcode 207. 课程表
207. 课程表 - 力扣(LeetCode)
你这个学期必须选修
numCourses门课程,记为0到numCourses - 1。在选修某些课程之前需要一些先修课程。 先修课程按数组
prerequisites给出,其中prerequisites[i] = [ai, bi],表示如果要学习课程ai则 必须 先学习课程bi。例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。请你判断是否可能完成所有课程的学习?如果可以,返回
true;否则,返回false。
入度数组数组记录每一门课的入度多少,通过bfs队列实现
参考代码:
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
int hasLearn=0;
queue<int>q;
vector<int>indegree(numCourses,0);
vector<vector<int>>gragh(numCourses);
for(int i=0;i<prerequisites.size();i++)
{
indegree[prerequisites[i][0]]++;
gragh[prerequisites[i][1]].push_back(prerequisites[i][0]);
}//初始化
for(int i=0;i<numCourses;i++)
{
if(indegree[i]==0)q.push(i);
}//插入入度为0的课
while(!q.empty())
{
int index=q.front();
q.pop();
hasLearn++;
for(auto p:gragh[index])//减少需要当前课的课的入度
{
--indegree[p];
if(indegree[p]==0)
{
q.push(p);
}
}
}
return hasLearn==numCourses;
}
};写在末尾
跟着做完这几题可以说是对排序算法入门了,后面要做的就是多练习多总结