论文:https://arxiv.org/pdf/2003.04618
代码:GitHub - autonomousvision/convolutional_occupancy_networks: [ECCV'20] Convolutional Occupancy Networks
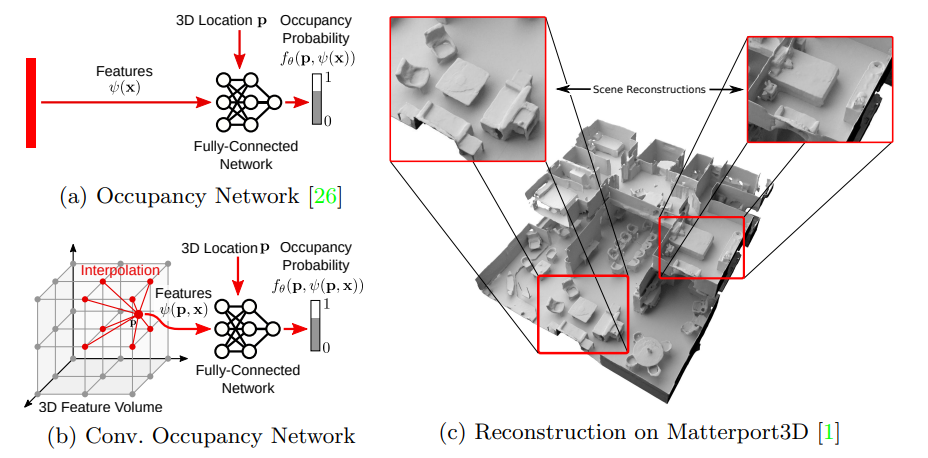
图 1:卷积占据网络。传统的隐式模型 (a) 由于其全连接网络结构,表现能力受到限制。我们提出了卷积占据网络 (b),利用卷积,从而实现可扩展且等变的隐式表示。我们通过线性插值在 3D 位置 查询卷积特征。与占据网络(ONet) 相比,所提出的特征表示 依赖于输入 和 3D 位置 。图 (c) 显示了在 Matterport3D 数据集上从一个噪声点云重建的两层建筑。
摘要:
最近,隐式神经表示在基于学习的3D重建中变得流行起来。尽管展示了有前景的结果,但大多数隐式方法仅限于相对简单的单个对象几何形状,并且无法扩展到更复杂或大规模的场景。隐式方法的关键限制因素是其简单的全连接网络架构,这不允许在观察中整合局部信息或结合诸如平移等变性等归纳偏置。在本文中,我们提出了卷积占据网络,这是一种更灵活的隐式表示,用于详细重建物体和3D场景。
通过结合卷积编码器和隐式占据解码器,我们的模型结合了归纳偏置,从而在3D空间中实现结构化推理。我们通过从噪声点云和低分辨率体素表示中重建复杂几何形状来研究所提出表示的有效性。我们通过实验证明,我们的方法可以实现单个对象的细粒度隐式3D重建,扩展到大型室内场景,并且可以从合成数据很好地泛化到真实数据。
主要贡献:
- 我们识别了当前隐式3D重建方法的主要限制。
- 我们提出了一种灵活的平移等变架构,使得从物体到场景层次的精确3D重建成为可能。
- 我们证明了我们的模型能够从合成场景泛化到真实场景,并能够泛化到新的物体类别和场景。
相关工作:
基于学习的3D重建方法可以根据它们使用的输出表示进行广泛分类。
体素: 体素表示是基于学习的3D重建最早期的表示之一【5, 46, 47】。由于体素表示的立方体内存需求,一些工作提出在多个尺度上操作或使用八叉树进行有效的空间分割【8, 14, 25, 37, 38, 42】。然而,即使使用自适应数据结构,体素技术在内存和计算方面仍然有限。
点云: 另一种3D重建的输出表示是3D点云,已在【9, 21, 34, 49】中使用。然而,基于点云的表示在处理点的数量方面通常受到限制。此外,它们无法表示拓扑关系。
网格: 一种流行的替代方法是使用神经网络直接回归网格的顶点和面【12, 13, 17, 20, 22, 44, 45】。虽然这些工作中的一些需要变形固定拓扑的模板网格,其他则导致带有自相交网格面的非水密重建。
隐式表示: 最近的隐式占据【3, 26】和距离场【27, 31】模型使用神经网络在给定任何3D点作为输入时推断占据概率或距离值。与上述需要离散化的显式表示(例如体素、点或顶点数量)相比,隐式模型连续表示形状,并且自然处理复杂的形状拓扑。隐式模型已被用于从图像学习隐式表示【23, 24, 29, 41】,编码纹理信息【30】,进行4D重建【28】,以及基于原语的重建【10, 11, 15, 32】。不幸的是,所有这些方法都仅限于相对简单的单个对象的3D几何形状,不能扩展到更复杂或大规模的场景。关键限制因素是简单的全连接网络架构,这不允许整合局部特征或结合平移等变性等归纳偏置。
值得注意的例外是PIFu【40】和DISN【48】,它们使用像素对齐的隐式表示来重建穿衣人【40】或ShapeNet对象【48】。虽然这些方法也利用了卷积,但所有操作都在2D图像域中进行,限制了这些模型到基于图像的输入和单个对象的重建。相比之下,在这项工作中,我们提出在物理3D空间中聚合特征,利用2D和3D卷积。因此,我们的以世界为中心的表示独立于相机视点和输入表示。此外,我们证明了隐式3D重建在场景级别的可行性,如图1c所示。
在并行工作中,Chibane等人【4】提出了一个与我们的卷积体积解码器相似的模型。与我们相比,他们仅考虑单一变体的卷积特征嵌入(3D),使用有损离散化进行3D点云编码,并且仅展示了单个对象和人类的结果,而不是完整的场景。在另一项并行工作中,Jiang等人【16】利用形状先验进行场景级隐式3D重建。与我们不同的是,他们使用3D点法线作为输入,并且在推理时需要优化。
方法:
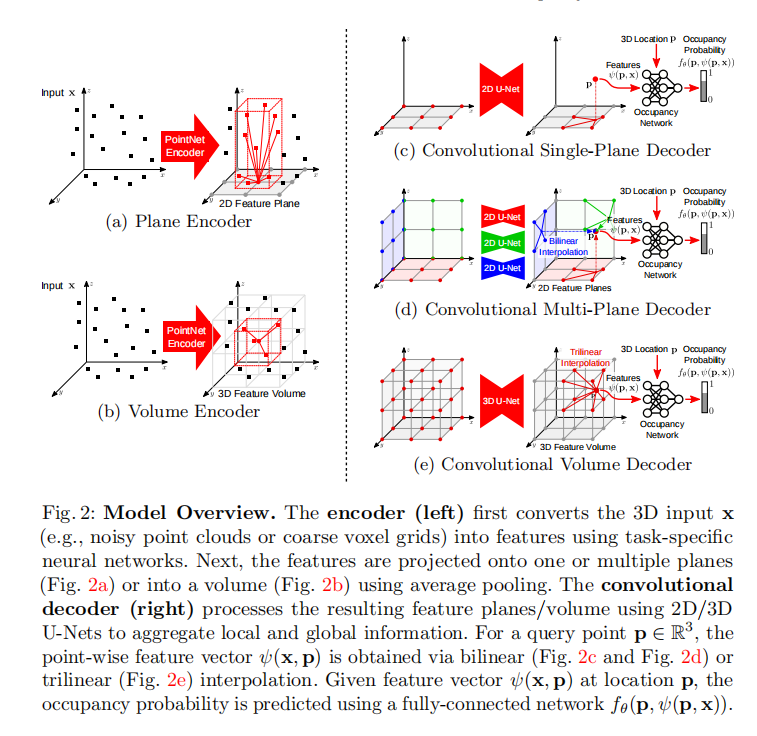
我们的目标是使隐式3D表示更加具有表现力。我们模型的概览如图2所示。我们首先将输入x(例如,一个点云)编码成2D或3D特征网格(左侧)。这些特征经过卷积网络处理,然后通过全连接网络解码为占据概率。我们在实验中研究平面表示(a+c+d)、体积表示(b+e)以及它们的组合。接下来,我们详细解释编码器(第3.1节)、解码器(第3.2节)、占据预测(第3.3节)和训练过程(第3.4节)。
3.1 编码器
虽然我们的方法与输入表示无关,但我们专注于3D输入,以展示我们的模型恢复精细细节和扩展到大场景的能力。更具体地说,我们假设输入x是噪声稀疏的点云(例如,来自结构运动或激光扫描),或者是粗糙的占据网格。
我们首先用一个与任务相关的神经网络处理输入x,以获得每个点或体素的特征编码。对于体素化的输入,我们使用一个单层3D CNN,对于3D点云,我们使用一个浅层的PointNet [35] 并进行局部池化。在获得这些特征之后,我们按照以下方式构建平面和体积特征表示,以包含局部邻域信息。
平面编码器:如图2a所示,对于每个输入点,我们执行正交投影到一个规范平面上(即,与坐标系的轴对齐的平面),我们将其离散化为分辨率为H × W像素单元。对于体素输入,我们将体素中心视为一个点并将其投影到平面上。我们使用平均池化来聚合投影到相同像素的特征,从而得到具有维度H × W × d的平面特征,其中d是特征维度。
在我们的实验中,我们分析了我们模型的两个变体:一个变体将特征投影到地面平面,另一个变体将特征投影到所有三个规范平面。虽然前者在计算上更有效率,但后者允许在z维度中恢复更丰富的几何结构。
体积编码器:虽然平面特征表示允许在较大的空间分辨率下进行编码(1282像素及以上),但它们局限于二维。因此,我们还考虑体积编码(见图2b),它更好地表示3D信息,但局限于较小的分辨率(通常在我们的实验中为323个体素)。与平面编码器类似,我们执行平均池化,但这次是针对落入同一个体素单元的所有特征,从而得到具有维度H × W × D × d的特征体积。
3.2 解码器
我们通过使用2D和3D卷积的Hourglass(U-Net)网络[6, 39]处理来自编码器的特征平面和特征体积,为我们的模型赋予了平移等变性,该网络由一系列下采样和上采样卷积组成,并带有跳跃连接,以整合局部和全局信息。我们选择U-Net的深度,使其感受野等于相应特征平面或体积的大小。
我们的单平面解码器(图2c)使用2D U-Net处理地面平面特征。多平面解码器(图2d)分别使用具有共享权重的2D U-Net处理每个特征平面。我们的体积解码器(图2e)使用3D U-Net。由于卷积操作具有平移等变性,我们的输出特征也具有平移等变性,从而实现了结构化推理。此外,卷积操作能够“修复”特征同时保留全局信息,从而实现了从稀疏输入进行重构。
3.3 占据预测
给定聚合的特征图,我们的目标是估计3D空间中任意点p的占据概率。对于单平面解码器,我们将每个点p正交投影到地面平面,并通过双线性插值查询特征值(图2c)。对于多平面解码器(图2d),我们通过对所有3个平面的特征求和来聚合来自3个规范平面的信息。对于体积解码器,我们使用三线性插值(图2e)。将输入x在点p处的特征向量表示为ψ(p, x),我们使用一个小型全连接的占据网络来预测点p的占据情况:
![]()
网络包括多个ResNet块。我们使用[29]的网络架构,将ψ添加到每个ResNet块的输入特征中,而不是之前工作中提出的更消耗内存的批量归一化操作[26]。与[29]不同,我们使用32作为隐藏层的特征维度。有关网络架构的详细信息可在补充材料中找到。
3.4 训练和推断
在训练时,我们在感兴趣的体积内均匀采样查询点p ∈ R 3,并预测它们的占据值。我们应用预测值ˆop和真实占据值op之间的二元交叉熵损失:
![]()
结论:
我们引入了卷积占据网络(Convolutional Occupancy Networks),这是一种将卷积神经网络的表现力与隐式表示的优势结合起来的新型形状表示方法。我们分析了2D和3D特征表示之间的权衡,并发现融合卷积操作有助于推广到未见类别、新颖的房间布局和大规模室内空间。我们发现我们的三平面模型在内存效率方面表现良好,对合成场景效果好,并允许更大的特征分辨率。相比之下,我们的体积模型在真实场景中表现出色,但消耗更多内存。
最后,我们指出我们的方法不具备旋转等变性,而且只在与定义的体素大小的倍数相关的平移中具有平移等变性。此外,合成数据和真实数据之间仍然存在性能差距。虽然本文的重点是基于学习的3D重建,在未来的工作中,我们计划将我们的新型表示方法应用于其他领域,如隐式外观建模和4D重建。