如何理解“堆”

堆是一种特殊的树，只要满足如下两点：

1. 堆是一个完全二叉树；

2. 堆中每个节点的值都必须>=（或<=）其子树中每个节点的值。

大顶堆：每个节点的值都>=子树中每个节点的值；

小顶堆：每个节点的值都<=子树中每个节点的值；

如何实现一个堆

要实现一个堆，先要知道，堆都支持哪些操作以及如何存储一个堆。

如下，用一个数组存储堆：

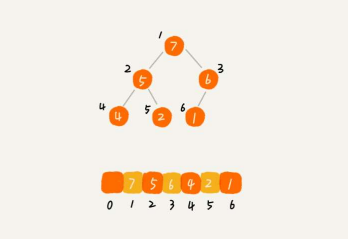
数组中下标为i的节点的左子节点，就是下标为i*2的节点，右子节点就是下标为i*2+1的节点，父节点就是下标为i/2的节点。

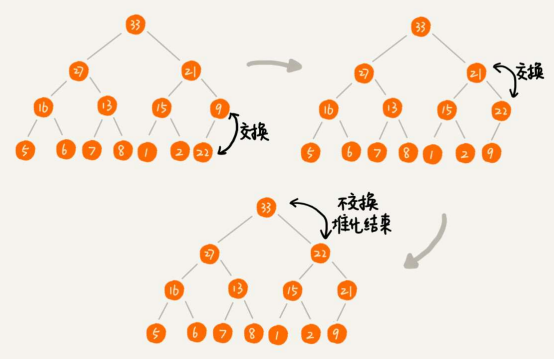
1. 往堆中插入一个元素

堆化（heapify）：把新元素插入堆的最后，然后调整堆，让其重新满足堆的特性。

堆化有两种：从下往上和从上往下

堆化非常简单，就是顺着节点所在的路径，向上或向下，对比，然后交换。

public class Heap {
    private int[] a; // 数组，从下标1开始存储数据
    private int n; // 堆可以存储的最大数据个数
    private int count; // 堆中已经存储的数据个数

    public Heap(int capicity) {
        a = new int[capicity + 1];
        n = capicity;
        count = 0;
    }

    public void insert(int data) {
        if (count >= n) return; // 堆满了
        ++count;
        a[count] = data;
        int i = count;
        while (i/2 > 0 && a[i] > a[i/2]) {
            swap(a, i, i/2); // 交换下标为i 和i/2 的两个元素
            i = i/2;
        }
    }
}