AStar(A*)算法核心思想( for unity)

news2024/10/6 6:04:51

AStar算法

算法思想
举例理解
核心代码

A* 算法，A* (A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。

注意:AStar的类应该作为一种单例类只提供调用方法，对节点的初始化都应该在节点类中完成

算法思想

1.创建两个列表用于维护节点，openList和closeList
openList用于存储所有已保存但是还未考察的节点
closeList用于存储已经访问的节点

2.只要openList中还存在未考察节点，就从中取出一个代价最低的节点作为当前节点。
3.如果当前节点是目标节点则说明一条合适的路径已经找到。如果不是，则开始为何该节点。
4.对不在closeList列表中的节点重新维护代价，然后放入openList中。
5持续2->4的过程。

举例理解

首先我们需要知道估价函数：F(N)=G(N) + H(N) AStar算法会不断维护节点的代价，已得到代价最小的一段路径
其中:G为是在状态空间中从初始状态到状态n的最小代价
H为是从状态n到目标状态的最小估计代价

以正方形节点为举例：
对于单位正方形，边长为1，对角线代价为√2 ≈1.1414
但是为了计算将代价都×10，我们规定在水平垂直方向上移动所需的代价为10，对角向方向上移动所需的代价为14.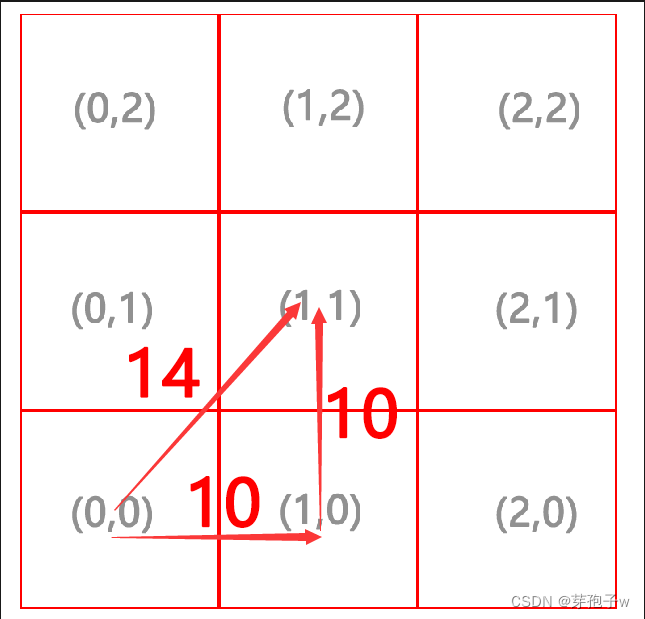 正方形节点代价
正方形节点的代价开销我会按如下格式标注
请添加图片描述
那么如果使用A*算法去寻找（0,0,）到（2,2)的路径，会发生什么呢？
第一次寻找：
开始时openList中只有（0，0）一个节点，所以直接找(0,0)的邻居，红色部分为（0,0）的邻居节点（一个正方形应该有8个邻居节点，但是也可以规定对角线方向上的节点不是邻居节点，但一般都不会这样做。）
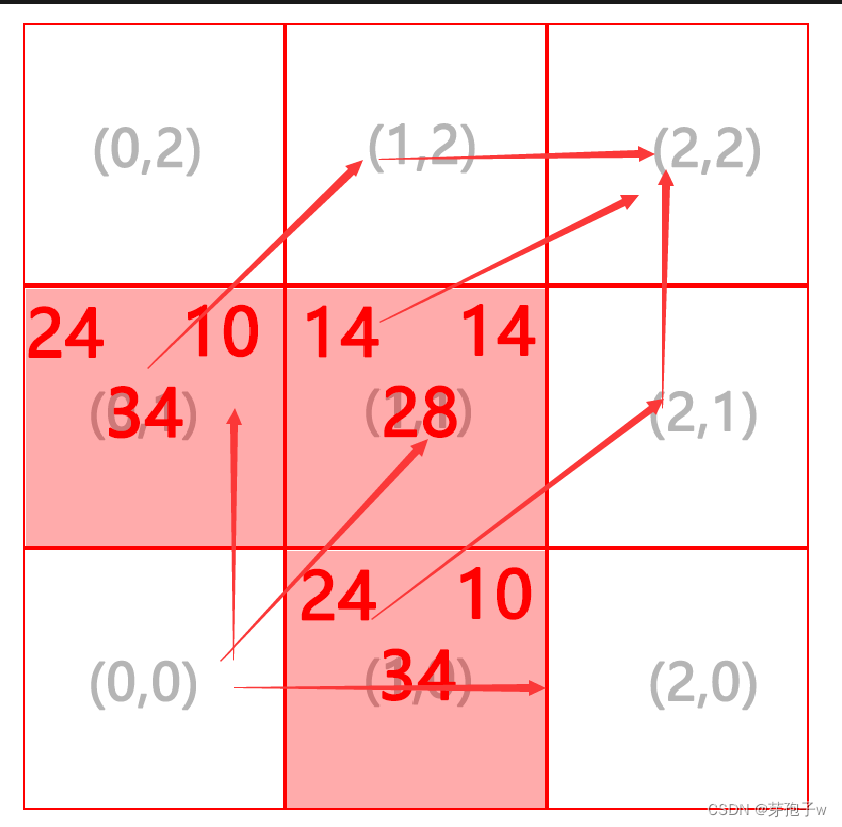
请添加图片描述
这三个邻居节点一开始都不存在与closeList中，所以把这三个邻居节点都放入openList中（保存节点时，不会考虑存入的节点代价，任意此刻代价较大的节点都会可能在经历几次查找之后变为openList最小的节点，这样我们的算法就可以“反悔”自己走过的路径）

第二次寻找：
此时，openList中有三个节点，也可以看出（1,1）的代价花费最小，所以我们把（1,1）节点拿出来
（1,1）的邻居节点为: (0,0), (1,0), (2,0), (0,1), (2,1),(0,2), (1,2), (2,2）
（0,0）节点已经位于closeList中，(1,0）和（0,1）位于openList中，所以这三个节点都不再重新计算（不退步，也不故意绕路）
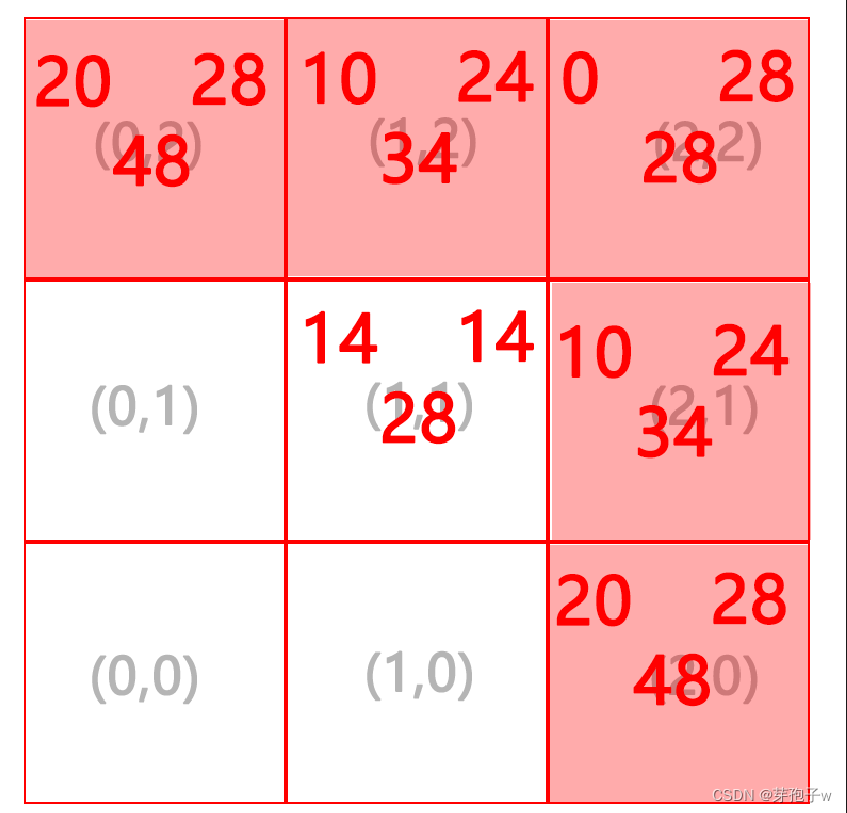
请添加图片描述
其实在进行这一步寻找时，在找到（2,2）节点时就会直接返回结果，我们也可以看到通过A*算法找到的节点代价是最小的，但是路径却不一定是唯一的（如果在上述正方形节点中，对角线方向上的节点不被视为邻居，那么可以有两条路径从（0,0）通向（2,2））

在正方形节点中计算F会用到曼哈顿方法花费

Vector2 dist =new Vector2Int(Mathf.Abs((int)pos.x - (int)other.pos.x), Mathf.Abs((int)pos.x- (int) other.pos.y));
int lowest =Mathf.Min(dist.x, dist.y);
int highest =Mathf.Max(dist.x, dist.y);
int horizontalMoveRequired =highest - lowest;
return lowest *14 + horizontalMoveRequired *10;

意思是对于一个直角三角形的路径，我们可以按照先走一个较短直角边的等腰直角三角形的对角线，然后在走一段两直角边之差的距离就可以了。
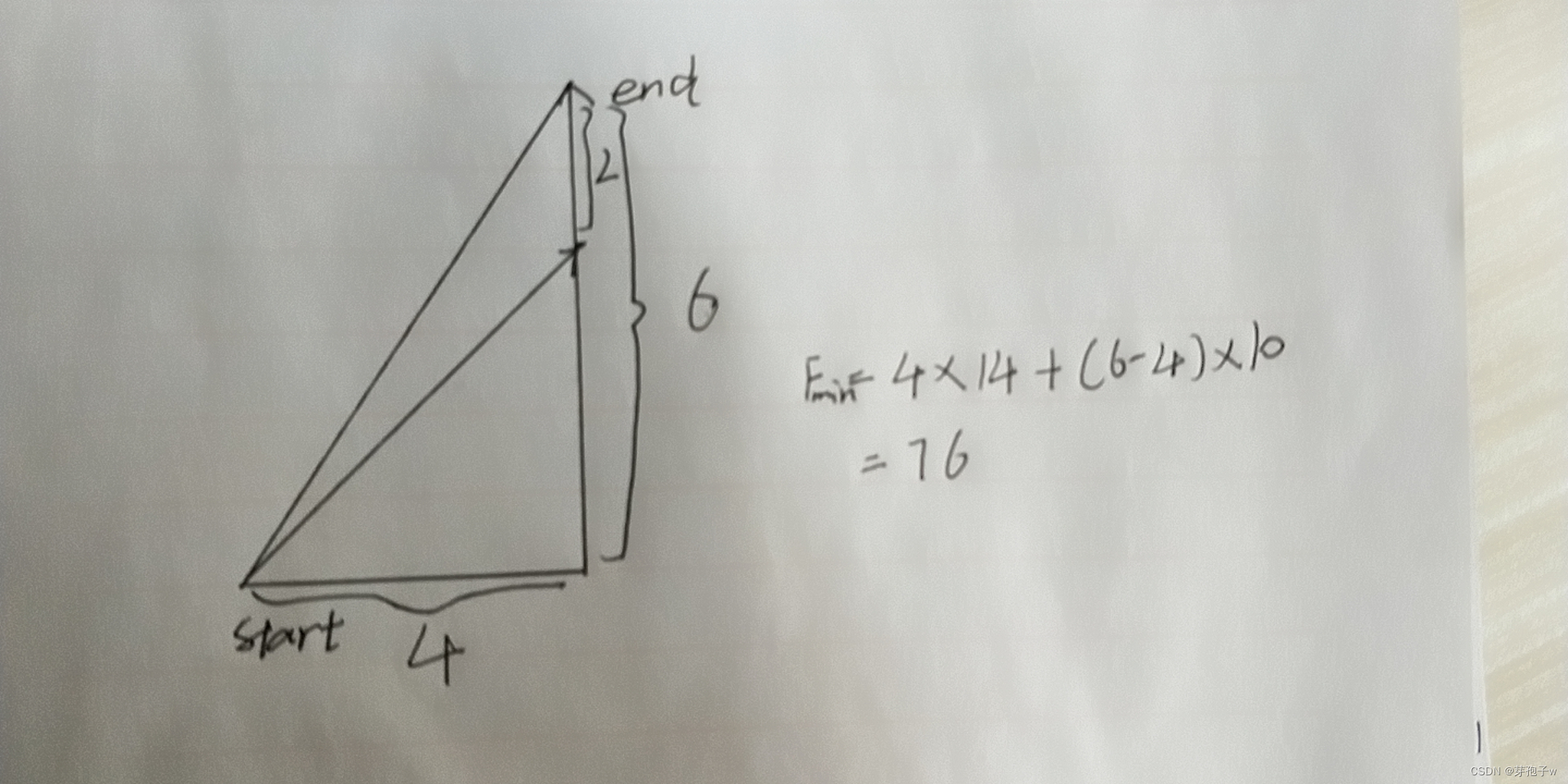
请添加图片描述

核心代码

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class AStar{

    public static AStar Instace;

    public List<NodeBase> _openList; //打开列表
    public List<NodeBase> _closeList; //关闭列表
    
    public List<NodeBase> FindPath(NodeBase startNode,NodeBase endNode){
        
        _openList = new List<NodeBase>(){ startNode}; //起始需要在打开列表中填入开始节点
        _closeList =new List<NodeBase>();

        //在这之前应该初始好所有的节点。
        startNode.G = 0;
        startNode.H = startNode.GetDistance(endNode.coords);
        
        while(_openList.Count > 0){
            NodeBase currentNodeBase = GetLowestFCostNode(_openList);
            if(currentNodeBase == endNode) return CalculatePath(endNode); 
           
            _openList.Remove(currentNodeBase);
            _closeList.Add(currentNodeBase);

            var tantativeGCost = currentNodeBase.G + currentNodeBase.GetDistance(endNode.coords); 
            //遍历邻居

            foreach(NodeBase n in currentNodeBase.Neighbours){
                if(_closeList.Contains(n)) continue;
                
                if(tantativeGCost < n .G && !_openList.Contains(n)){
                    n.father =currentNodeBase;
                    n.G= tantativeGCost;
                    n.H= n.GetDistance(endNode.coords);
					
                    _openList.Add(n);
                }
            }
        }
        return CalculatePath(endNode); //调用计算路径的函数返回结果序列
    }


    //得到Fcost最低的一个点
    private NodeBase GetLowestFCostNode(List<NodeBase> nodes){
        NodeBase lowe![请添加图片描述](https://img-blog.csdnimg.cn/0127049aecc5498d8cc9f14a51ddc5d5.png)
stFcostNode = nodes[0];
        foreach(Node n  in nodes){
            if(n.F < lowestFcostNode.F){
                lowestFcostNode = n;
            }
        }
        return lowestFcostNode;
    }


    //计算结果路径路径
    private List<NodeBase> CalculatePath(NodeBase node){
        List<NodeBase> nodeBases = new List<NodeBase>();
        while(node != null){
            nodeBases.Add(node);
            node=node.father;
        }
        nodeBases.Reverse();
        return nodeBases;
    }
}