1、递归实现指数型枚举
从 1∼n 这 n个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 1个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
1 ≤ n ≤ 15
输入样例:
3输出样例:
3
2
2 3
1
1 3
1 2
1 2 3递归搜索树:
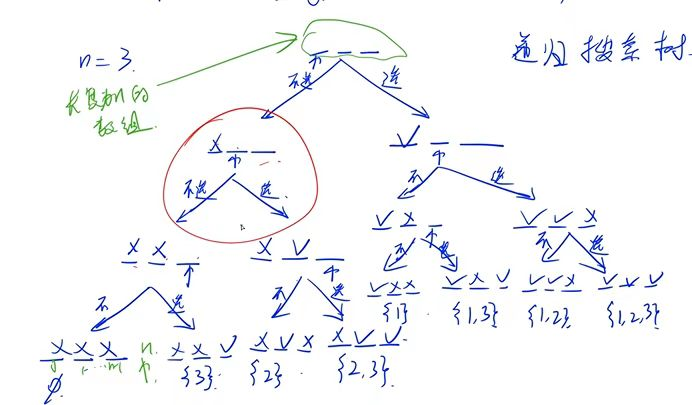
AC代码:
package 做题;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
public class Main
{
static final int N = 16;
static BufferedWriter wr;
static int st[] = new int[N];
static int n;
public static void dfs(int u) throws Exception //第几层就是筛选第几个数字
{
if(u > n) //不可以有等号,如果有等号会少一层递归,即最后一层无法递归
{
for(int i = 1 ; i <= n ; i ++) // 从1到n选择
{
if(st[i] == 1) wr.write(i+" ");// 把选的数打印出来
}
wr.write("\n");
return;
}
// 不选这个数字
st[u] = 2;
dfs(u + 1);
st[u] = 0;
// 选这个数字
st[u] = 1;
dfs(u + 1);
st[u] = 0;
}
public static void main(String[] args) throws Exception, IOException
{
BufferedReader rd = new BufferedReader(new InputStreamReader(System.in));
wr= new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(rd.readLine().trim());
dfs(1);
wr.flush();
wr.close();
rd.close();
}
}2、递归实现排列型枚举
把 1∼n 这 n个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入格式
一个整数 n。
输出格式
按照从小到大的顺序输出所有方案,每行 1个。
首先,同一行相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。
数据范围
1≤n≤9
输入样例:
3输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1递归搜索树:
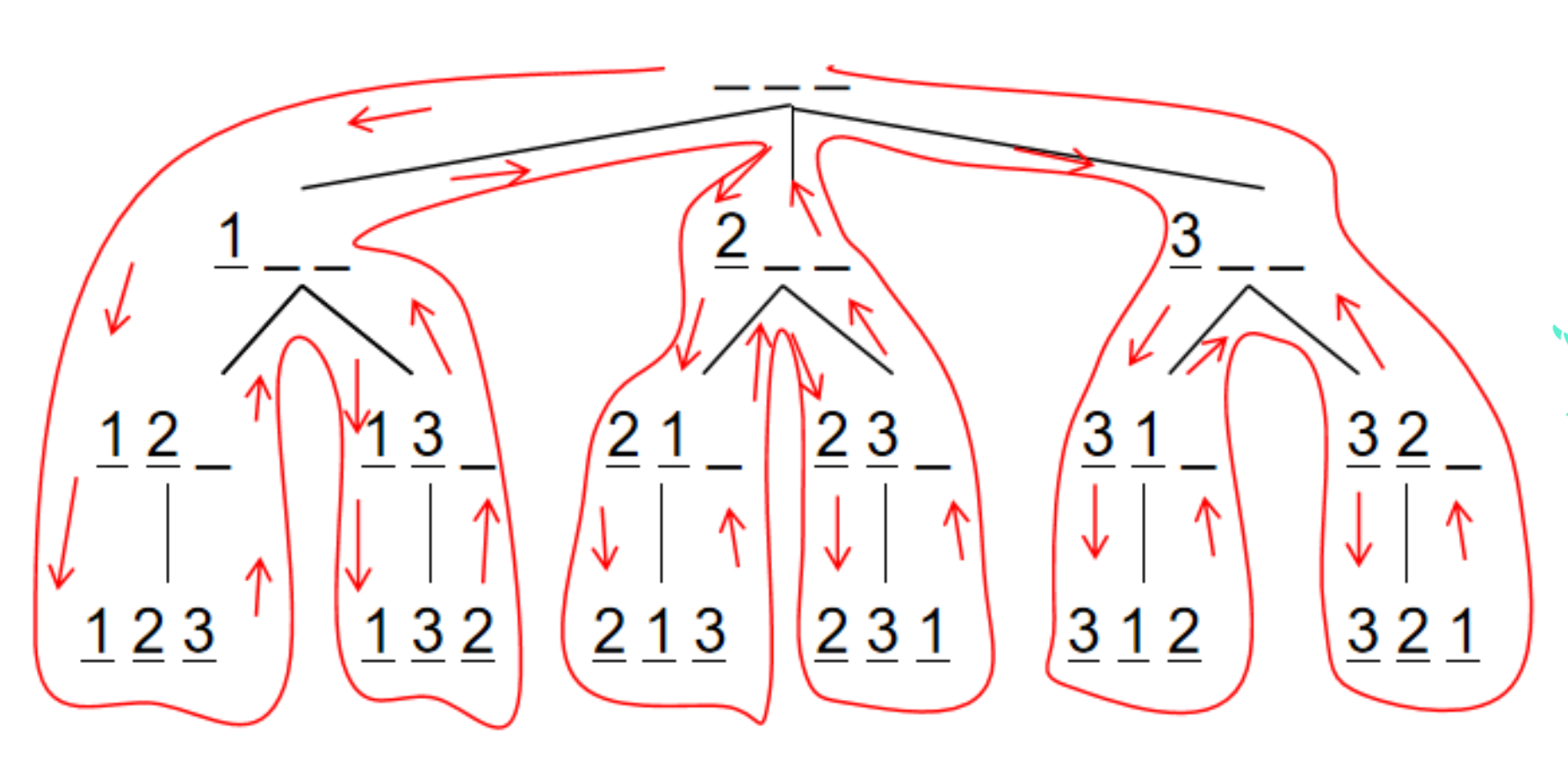
AC代码:
package 做题;
import java.awt.Taskbar.State;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
public class Main
{
static final int N = 16;
static BufferedWriter wr;
static int state[] = new int[N];// 0 表示还没放数,1~n表示放了哪个数
static boolean used[] = new boolean[N];// true表示用过,false表示还未用过
static int n;
public static void dfs(int u) throws Exception
{
if(u > n) // 边界
{
for(int i = 1 ; i <= n ; i ++) wr.write( state[i] + " "); // 打印某个方案
wr.write("\n");
return;
}
// 依次枚举每个分支,即当前位置可以填哪些数
for(int i = 1 ; i <= n ; i ++)
{
if(!used[i])
{
state[u] = i;
used[i] = true;
dfs(u + 1);
// 恢复现场
state[u] = 0;
used[i] = false;
}
}
}
public static void main(String[] args) throws Exception, IOException
{
BufferedReader rd = new BufferedReader(new InputStreamReader(System.in));
wr= new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(rd.readLine().trim());
dfs(1);
wr.flush();
wr.close();
rd.close();
}
}3、简单斐波那契
以下数列 0 1 1 2 3 5 8 13 21 ... 被称为斐波纳契数列。 这个数列从第 3项开始,每一项都等于前两项之和。输入一个整数 N,请你输出这个序列的前 N项。
输入格式
一个整数 N。
输出格式
在一行中输出斐波那契数列的前 N
项,数字之间用空格隔开。
数据范围
0<N<46
输入样例:
5输出样例:
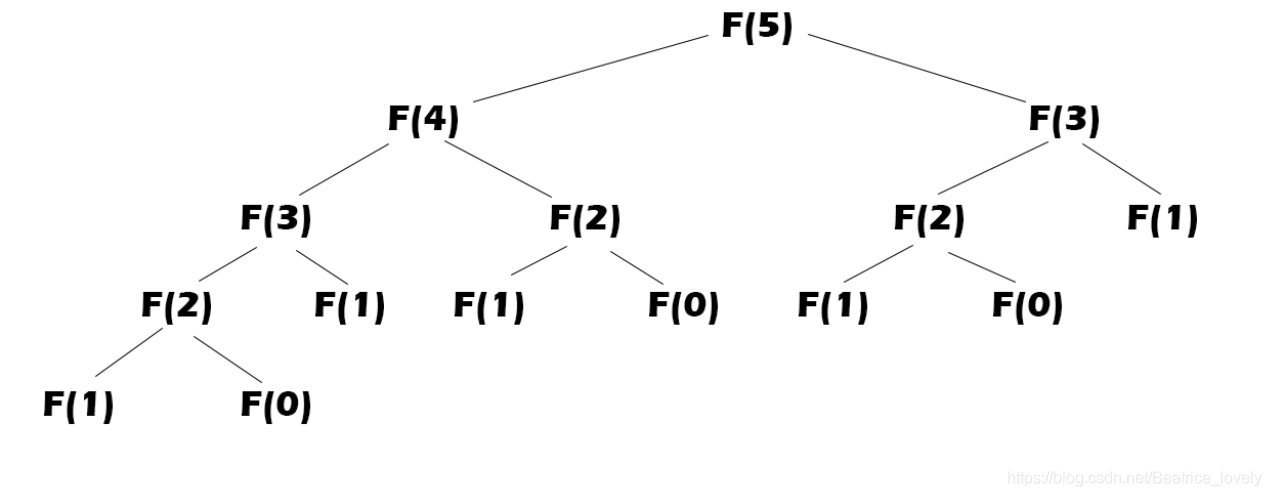
0 1 1 2 3递归搜索树:
(每个f(x)的最底层到f(0)或者f(1),因为这样才能算出值来)
package 做题;
import java.awt.Taskbar.State;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
public class Main
{
static final int N = 50;
static BufferedWriter wr;
static int a[] = new int[N];
static int n;
static void dfs(int u) throws Exception
{
if(u == n - 1) return; // 因为a[0]和a[1]有初值,一上来就更新了a[2],例如,如果计算f(5)(n等于5)即a[4](a[4] = a[3]和a[2]在u = 2的时候更新),更新完后,在u = 3的时候return,结束值的更新,确实够用了,但是如果n = 1,n - 2 = -1,u从主函数第一次进去dfs函数的时候等于0,u只递增,不可能是负数,所以会无限递归,直到栈爆,所以位置需要偏移一下,u == n - 1的时候结束递归来应对n == 1,多递归一层更新新的数也无所谓,寄不了
a[u + 2] = a[u + 1] + a[u];
dfs(u + 1);
}
public static void main(String[] args) throws Exception, IOException
{
BufferedReader rd = new BufferedReader(new InputStreamReader(System.in));
wr= new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(rd.readLine().trim());
a[0] = 0;
a[1] = 1;
dfs(0);
for(int i = 0 ; i < n ; i ++) wr.append(a[i] + " ");
wr.flush();
wr.close();
rd.close();
}
}