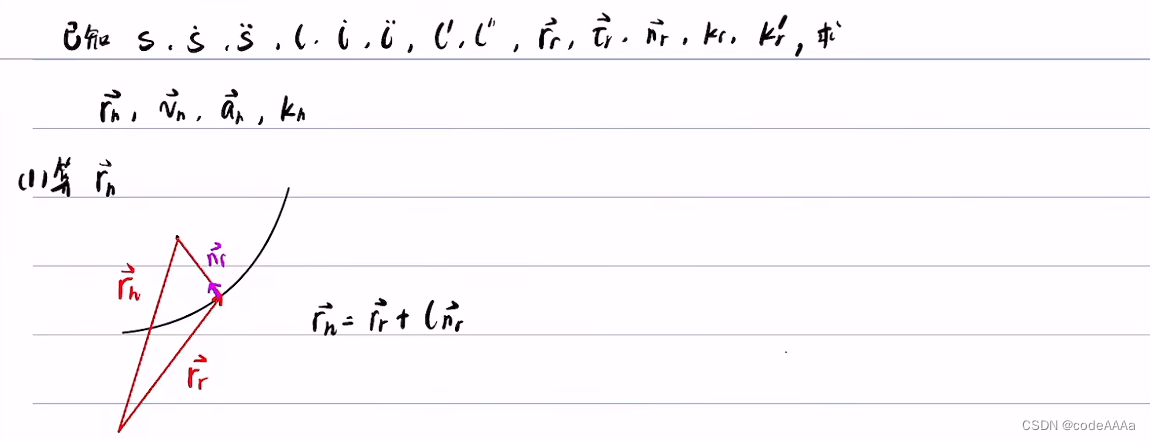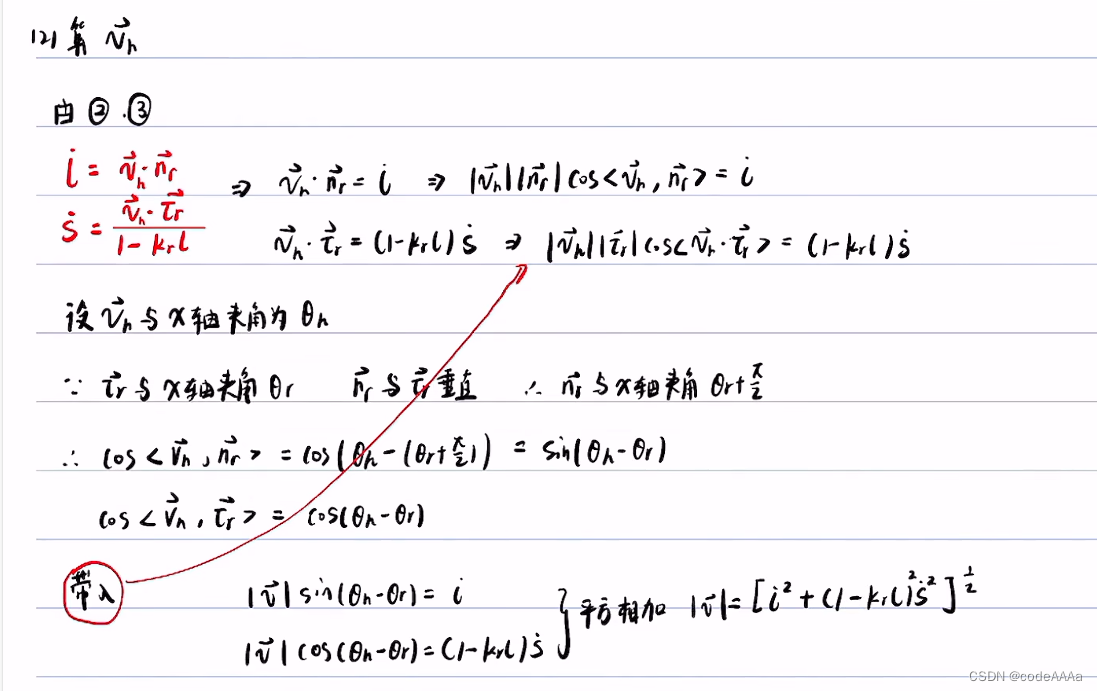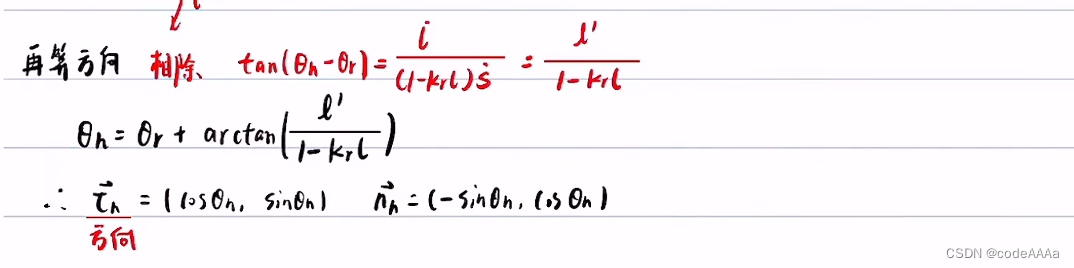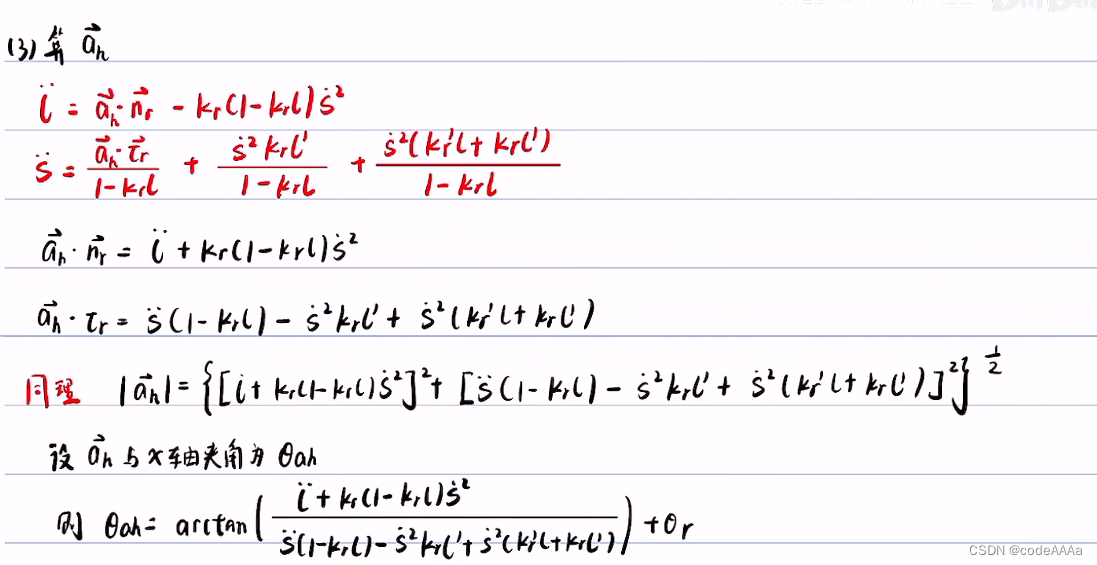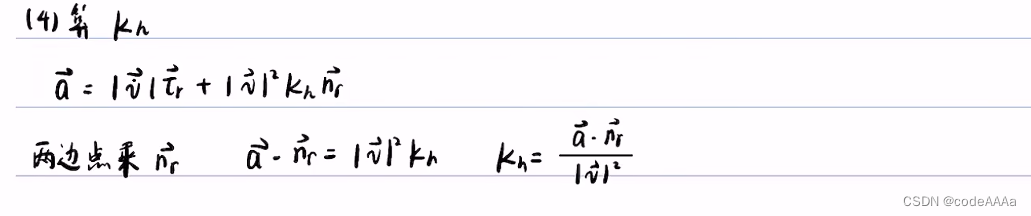以下内容来自b站up主忠厚老实的老王,视频链接:自动驾驶决策规划算法序章 总纲与大致目录_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1hP4y1p7es/?spm_id_from=333.999.0.0&vd_source=d36e625f376908cfa88ef5ecf2fb0ed8侵删。
https://www.bilibili.com/video/BV1hP4y1p7es/?spm_id_from=333.999.0.0&vd_source=d36e625f376908cfa88ef5ecf2fb0ed8侵删。
决策规划算法概述



数学基础
五次多项式


 其中隐含的限制就是f(t)的定义域和值域都应该是实数,因为s和t都是真实空间中的轨迹和时间坐标,不能有虚数。
其中隐含的限制就是f(t)的定义域和值域都应该是实数,因为s和t都是真实空间中的轨迹和时间坐标,不能有虚数。
要想使得上面的那个jark最小,积分号中是平方项,也就是当其为0时最小,也就是f(t)的三阶导数为0,也就是f(t)是二次或者二次以下的函数时,三阶导数才为0。





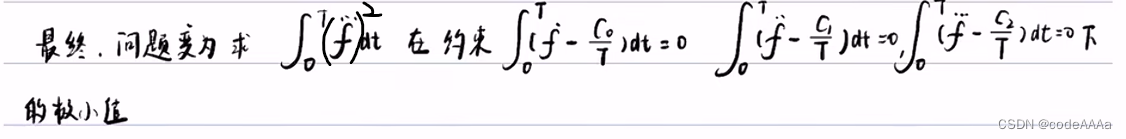
也就是求泛函![]() 在后面的那三个约束条件下极小值对应的f(t)。
在后面的那三个约束条件下极小值对应的f(t)。


上面把一个带约束的泛函化成了一个无约束的泛函,但是L和f点、f两点、f三点都有关,不能直接使用上面只能处理一阶导数的欧拉——拉格朗日方程。要使用广义的欧拉——拉格朗日方程:

 凸优化
凸优化



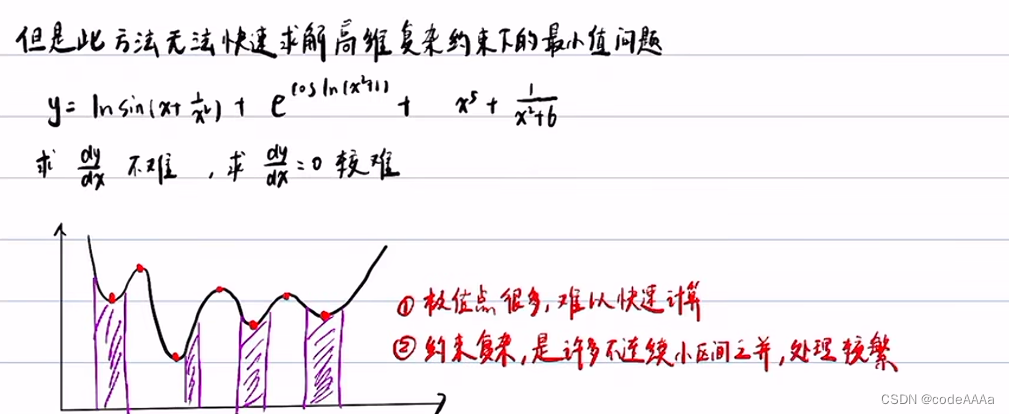
所以一般求复杂函数在复杂约束条件下的最小值问题都采用迭代法。迭代法的求解速度要比求导法快很多。

以梯度下降法为例说明大概原理:

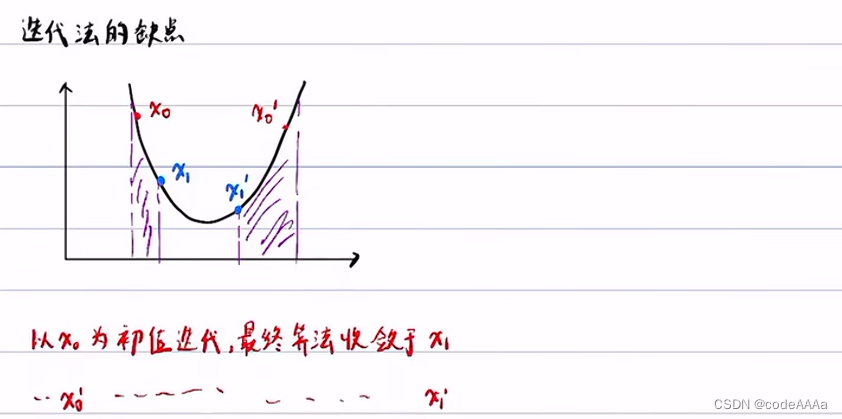
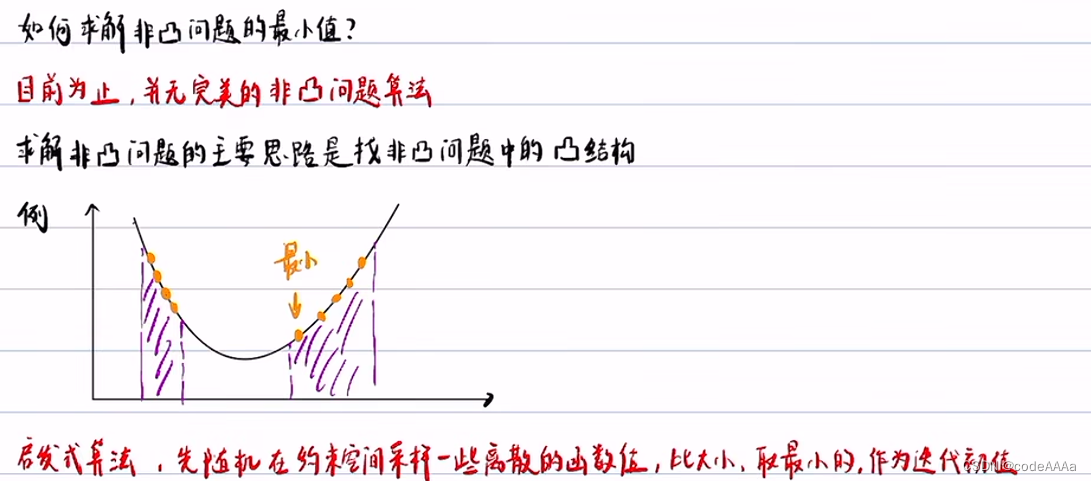
 紫色区域是约束,所以迭代法对初值比较敏感,有可能收敛到局部最小值。
紫色区域是约束,所以迭代法对初值比较敏感,有可能收敛到局部最小值。
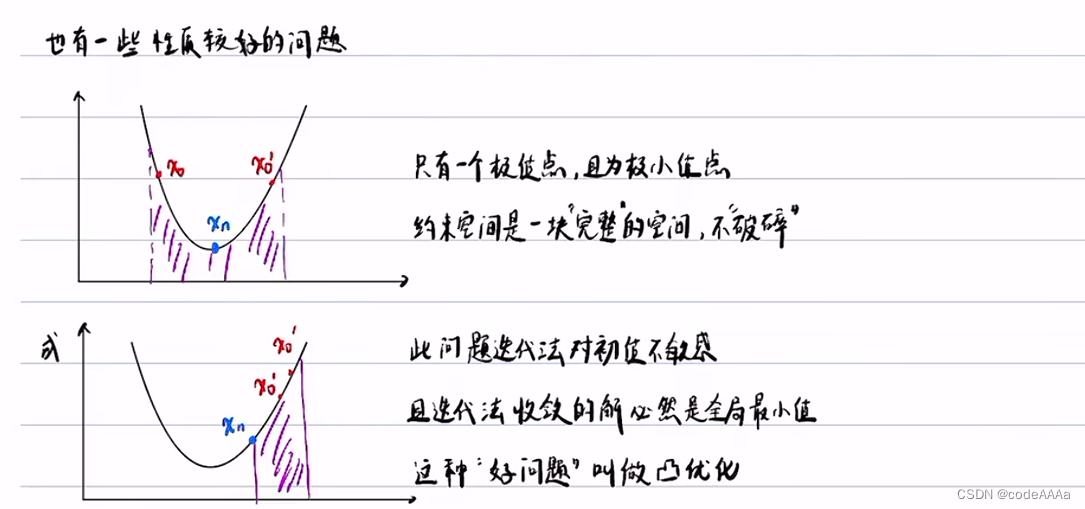



凸优化是最简单的非线性规划方法。自动驾驶的规划求解不是一个凸优化问题,凸优化必须满cost function是一个凸函数,约束空间是一个凸空间,以避障工况为例:



整个过程就是:

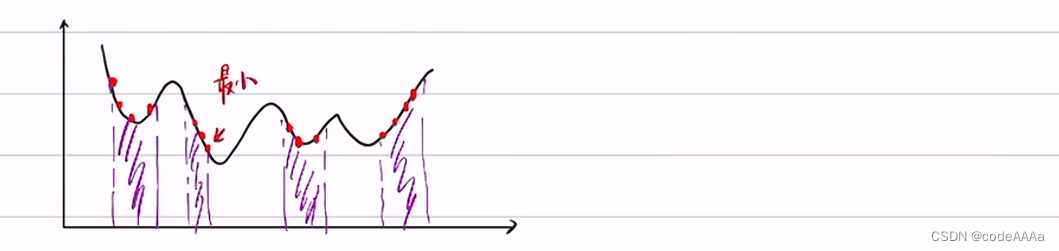
上述方法也有一定的缺点:

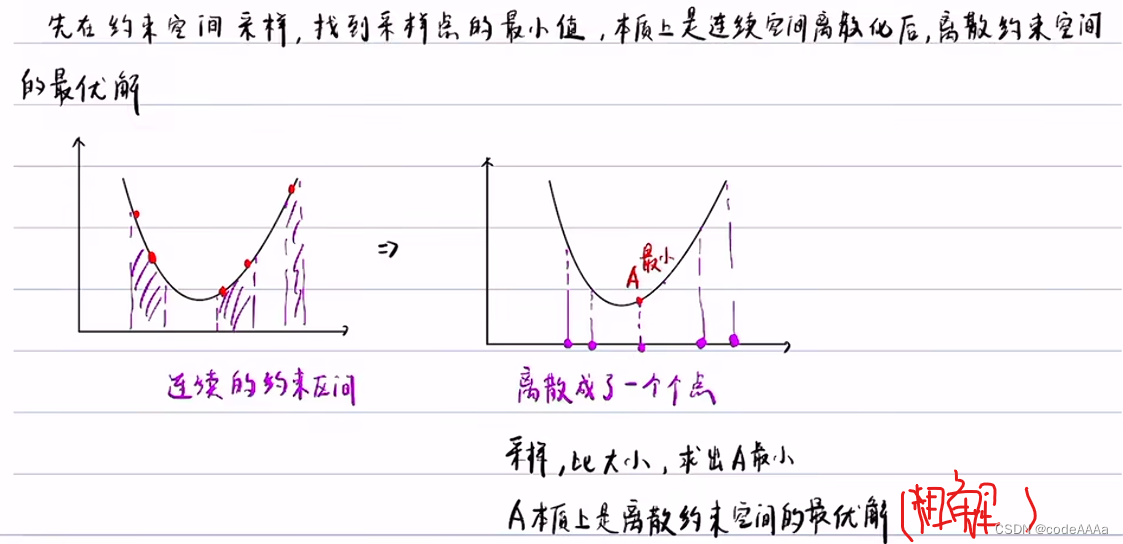
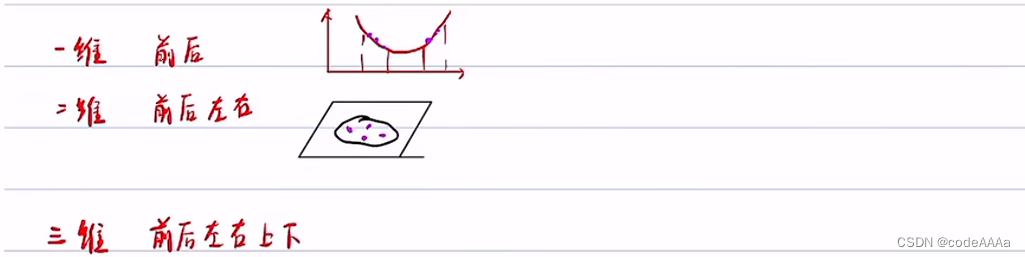
采样点少的话会比较容易收敛到局部最优,采样点多的话会发生维度灾难,如下:
frenet坐标系和Cartesian坐标系坐标转换
概述和基本量





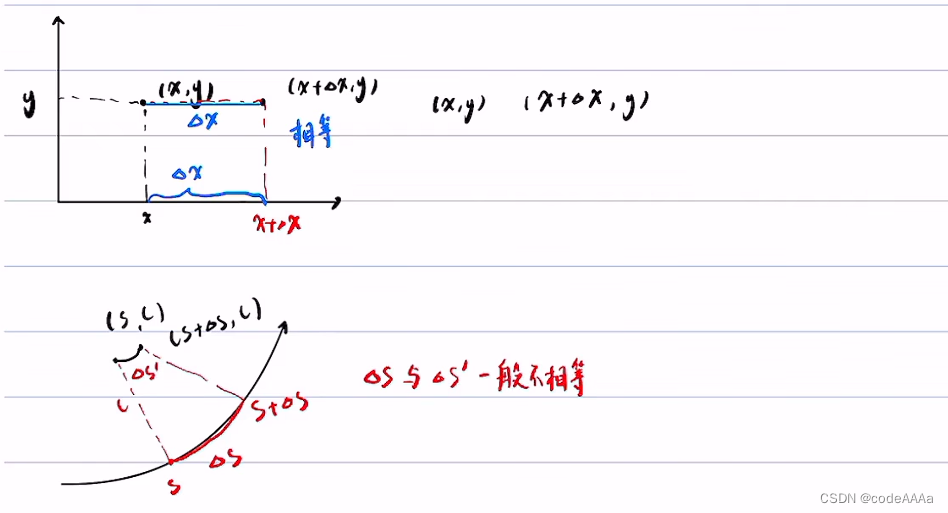

也就是在直角坐标系下想对一个函数求导,那它只有一个dx,这个dx是不区分点在x坐标上的位移还是点的实际位移在x坐标上的分量,因为这两者一样;但是在frenet坐标系中,它们是一样的所以在frenet坐标系中会有d/ds和d/dsx之分。在直角坐标系中可能只有一个dx,但是在frenet坐标系中,可能会有多个ds,举例说明如下:

这里使用dsx和ds来区分不同的s,在很多推导教程中可能中只用ds,会造成理解困难。
预备知识1

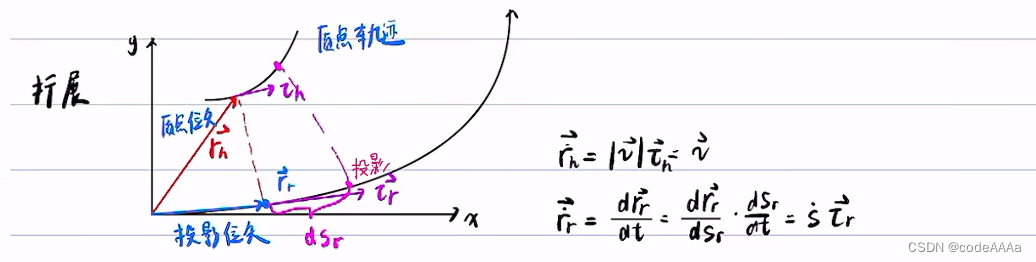
证明这个质点位矢r的导数等于v的模乘以τ,τ是质点在切线方向的单位向量。

当dt趋近于0时,ds和dr无限的接近,比值为1,方向会无限的趋近于在位矢r处的切线方向,也就是τ。
 预备知识2:frenet坐标系
预备知识2:frenet坐标系

其中ds是黑色曲线的弧微分,证明如下:

其中τ+dτ和τ以及dτ形成的三角形是一个等腰三角形,可以求出dτ的大小(也即使dτ的模),方向趋近于τ的法线方向。
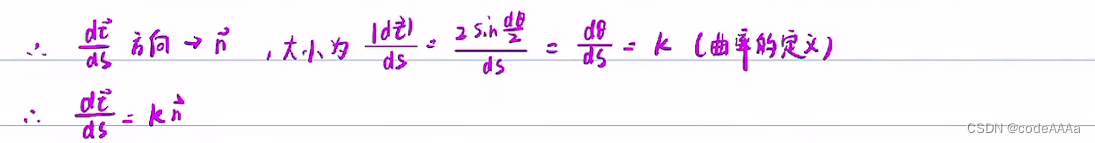 其中当dτ无限趋近于0时,sin(dθ/2)等价无穷小于(dθ/2)。
其中当dτ无限趋近于0时,sin(dθ/2)等价无穷小于(dθ/2)。
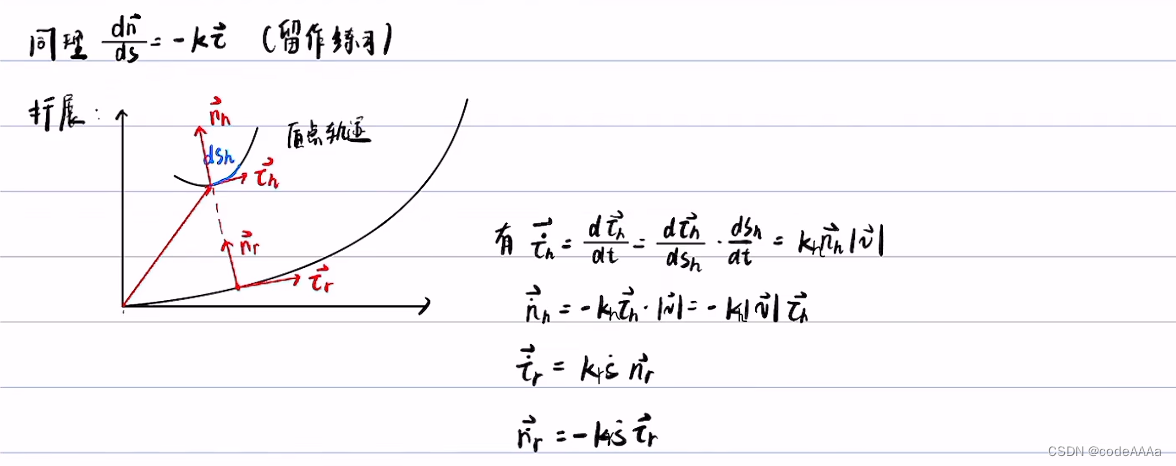
其中 kh是质点轨迹的曲率,kr是道路中心线的曲率,这里的曲率都是在直角坐标系下的曲率。

这里的ds指的是frenet坐标轴下的弧微分。

其中ρ是曲率半径,法向加速度是向心加速度。
预备知识总结
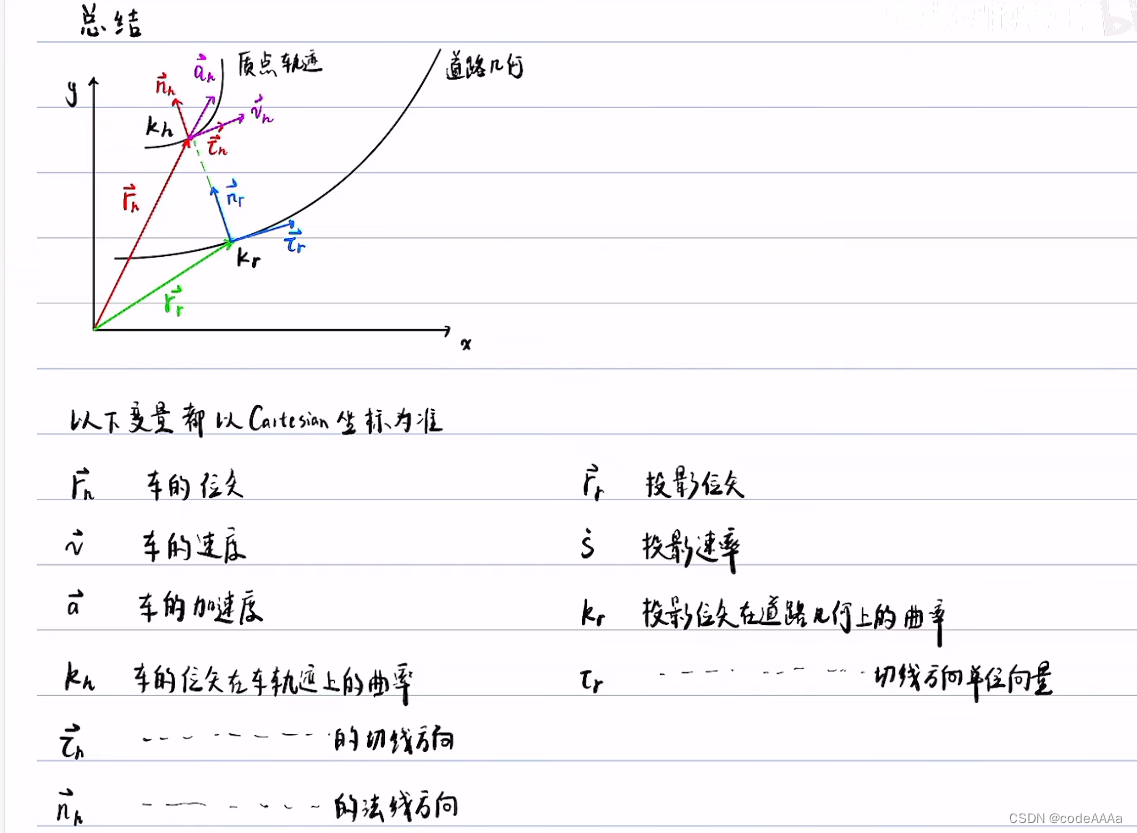


坐标转换(从直角坐标转为frenet坐标)
下面的问题就是已知在笛卡尔坐标系下的![]() ,以及frenet坐标系下的坐标起点
,以及frenet坐标系下的坐标起点![]() ,算这个点在frenet坐标系下的
,算这个点在frenet坐标系下的![]() ,其中
,其中![]() 。
。

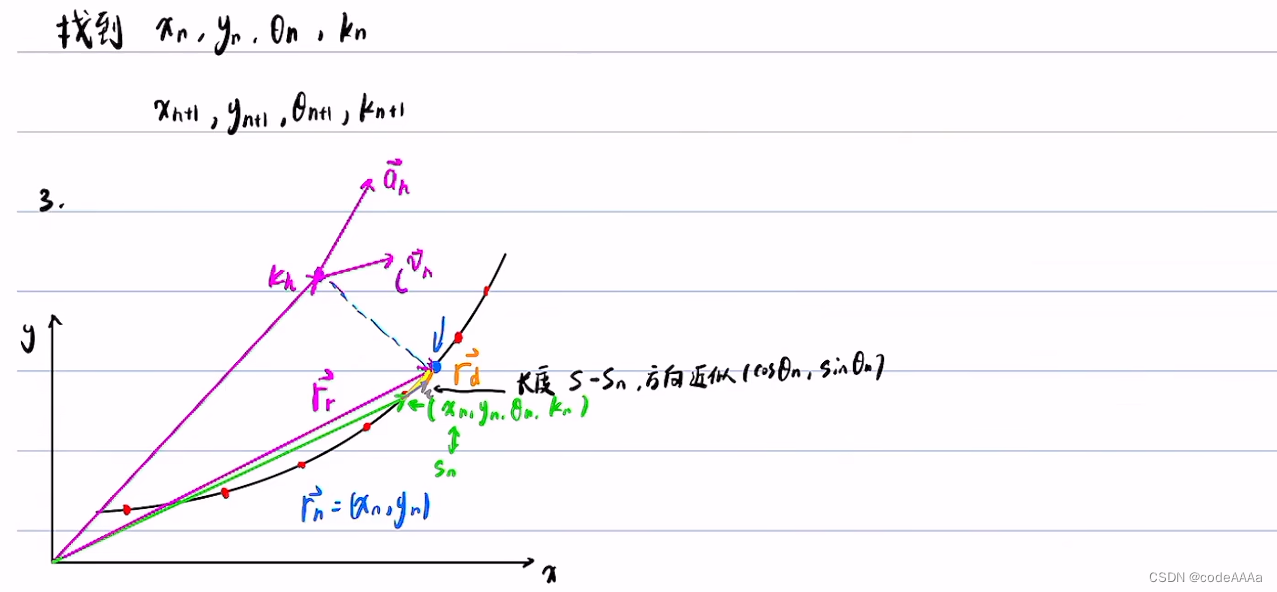
其中向量三角形是黄色区域,由向量三角形可以得到核心的公式:
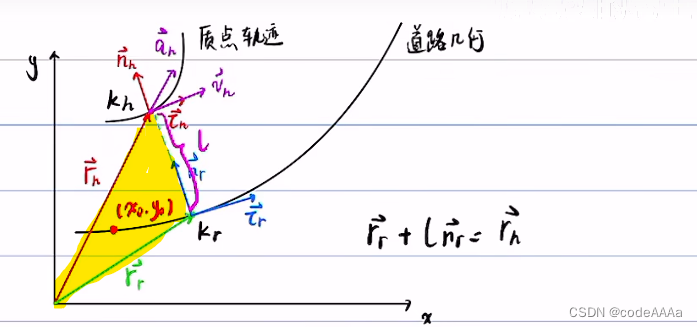
得到上面的核心公式,可以该公式和微积分依次求出![]() ,但是这个公式还不能直接使用,因为只知道rh,rr和nr未知,此时要找到投影点的相关信息。
,但是这个公式还不能直接使用,因为只知道rh,rr和nr未知,此时要找到投影点的相关信息。
投影点及其相关的信息的确定方法如下:

最后计算得到rr的原理如下:

为什么可以![]() 原理如下:
原理如下:


至此投影点的信息已经基本求值完毕。
下面可以使用上面的核心公式来计算相关量。
s的计算方法是从离散规划点起点开始把各个点的长度累加起来一直累加到投影点(xr,yr)为止。也就是以直线长度近似代替弧长:


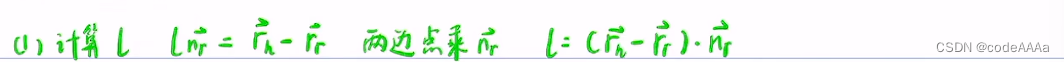

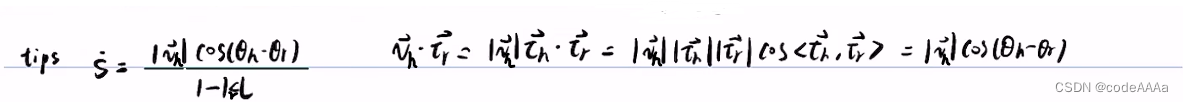




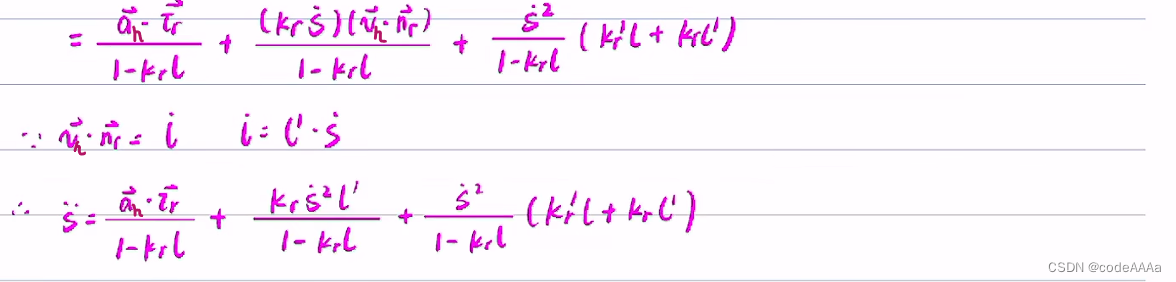

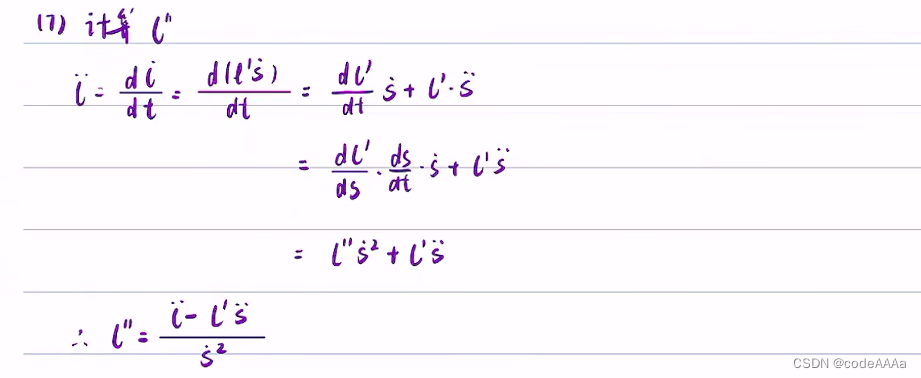
小结
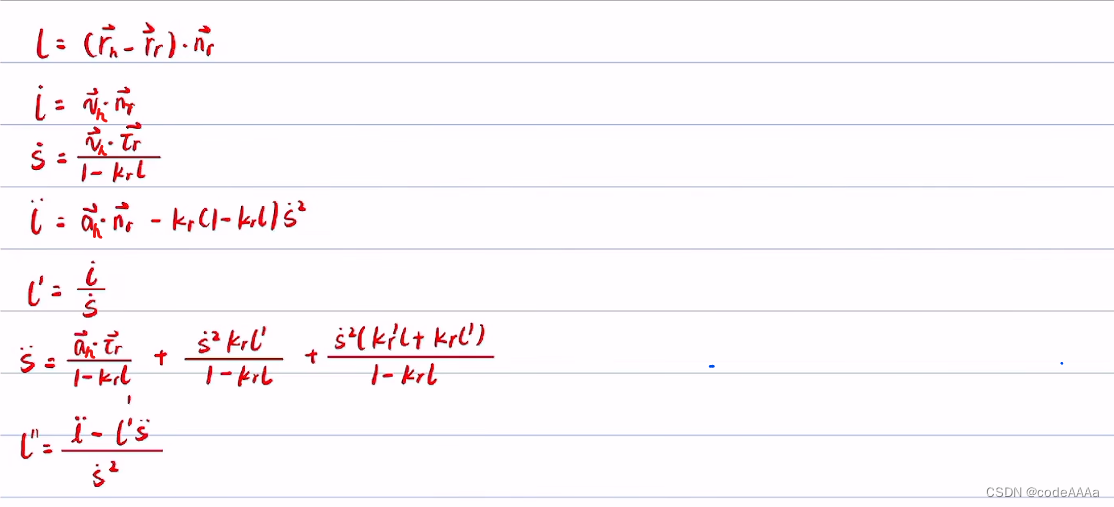
坐标变换(从frenet转换到直角坐标)