提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

目录

前言

一、Delaunay三角形

二、使用步骤

1.Bowyer-Watson算法

2.算法步骤

三、动画演示

四、核心代码

五、对比matlab自带函数和我们的算法：

总结

---

前言

前一篇文章《Matlab三角剖分插值问题分析（二）_matlab 空间面的三角剖分-CSDN博客》，讲的是使用剖分后的结果进行不规则的散点插值，这篇文章主要是讲如何形成剖分

---

一、Delaunay三角形

给定平面上的一组点集 P，Delaunay 三角剖分是将点集划分成若干个不重叠的三角形，使得任何一个三角形的外接圆不包含其他点。

有很多博客详细描述了定义和性质，我这边就不详细描述了。

Delaunay三角剖分——BW算法-CSDN博客

Delaunay三角剖分算法_delaunay 三角剖分算法-CSDN博客

二、使用步骤

1.Bowyer-Watson算法

Bowyer-Watson算法是一种增量算法。它的工作原理是将点一次一个地，添加到所有点的子集的Delaunay三角剖分中。每次插入新点后，任何外接圆包含新点的三角形都被删除，留下一个星形多边形孔，然后使用新点重新三角化。

2.算法步骤

Bowyer-Watson算法是一种用于构建Delaunay三角剖分的增量算法。该算法通过逐步添加点并调整三角剖分来保持Delaunay性质。以下是Bowyer-Watson算法的基本步骤

1. 初始三角剖分：

   • 创建一个足够大的超级三角形，覆盖所有要处理的点。
   • 该超级三角形的顶点应位于所有点之外，以确保初始三角剖分包含所有点。

2. 逐点插入：

   • 对每个点进行以下操作：
     1. 找到所有包含该点的三角形（即该点在这些三角形的外接圆内）。
     2. 移除这些三角形。
     3. 创建新三角形，将新点与移除三角形的相邻顶点连接。

3. 删除超级三角形相关的三角形：

   • 移除所有包含超级三角形顶点的三角形，得到最终的Delaunay三角剖分。

下是Bowyer-Watson算法的伪代码引自 Delaunay三角剖分——BW算法-CSDN博客

 1 function BowyerWatson (pointList)
 2     // pointList is a set of coordinates defining the points to be triangulated
 3     triangulation := empty triangle mesh data structure
 4     add super-triangle to triangulation // must be large enough to completely contain all the points in pointList
 5     for each point in pointList do // add all the points one at a time to the triangulation
 6         badTriangles := empty set
 7         for each triangle in triangulation do // first find all the triangles that are no longer valid due to the insertion 对应第2步：新插入点是否在三角形外接圆中
 8             if point is inside circumcircle of triangle
 9                 add triangle to badTriangles
10         polygon := empty set
11         for each triangle in badTriangles do // find the boundary of the polygonal hole 比如图中的ABCD
12             for each edge in triangle do
13                 if edge is not shared by any other triangles in badTriangles
14                     add edge to polygon
15         for each triangle in badTriangles do // remove them from the data structure
16             remove triangle from triangulation
17         for each edge in polygon do // re-triangulate the polygonal hole
18             newTri := form a triangle from edge to point
19             add newTri to triangulation
20     for each triangle in triangulation // done inserting points, now clean up 插完所有点了，现在清理掉外围的三角形，如下图中的蓝色三角形之外的三角形。
21         if triangle contains a vertex from original super-triangle
22             remove triangle from triangulation
23     return triangulation

三、动画演示

如果对原理理解困难，youtube有个动画演示，讲的不错，我这边截下来分解动作再说说

https://www.youtube.com/watch?v=GctAunEuHt4&t=1s

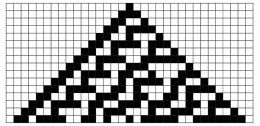
要找上面四个点的德劳内三角剖分

先构造一个超级三角形，把所有点都包含在内

选择一个点，在你所有的三角形集内找一个三角形，它的外接圆包含我们这个点，当下只有超级三角满足

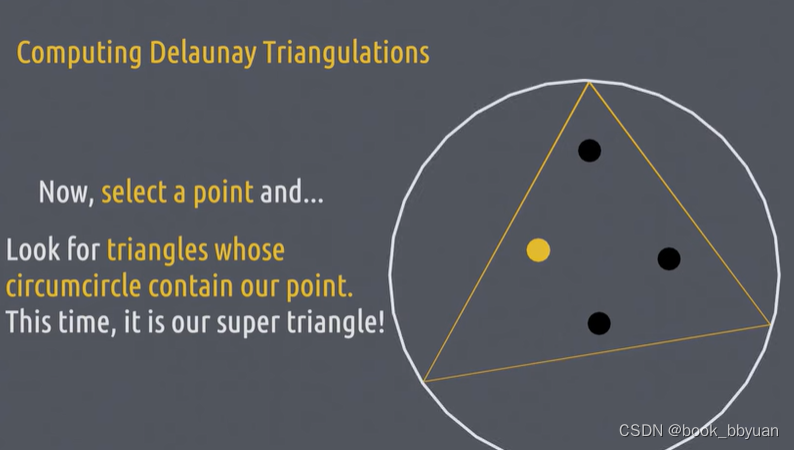
这不是我们想要的结果（显然超级三角形不是得劳内三角形，不满足只含三个点）我们把此点和三角形的三个顶点都连接上，形成新的三角形，都加到集内

现在处理下面的两个点，在三角形集内找到所有（外接圆）包含这个点的三角形，有两个

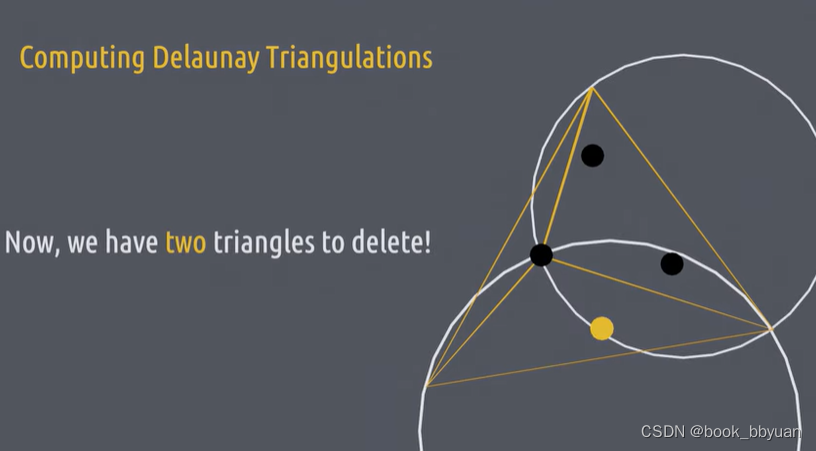
对这俩三角形处理，删除掉他们的公共边，形成“星形多边形”

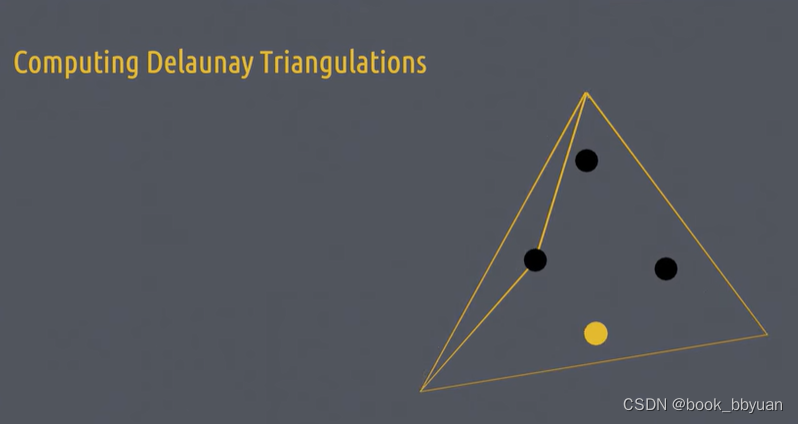
同时这个黄点也要连接上所有的顶点，形成的新的四个小三角形也要加到集内

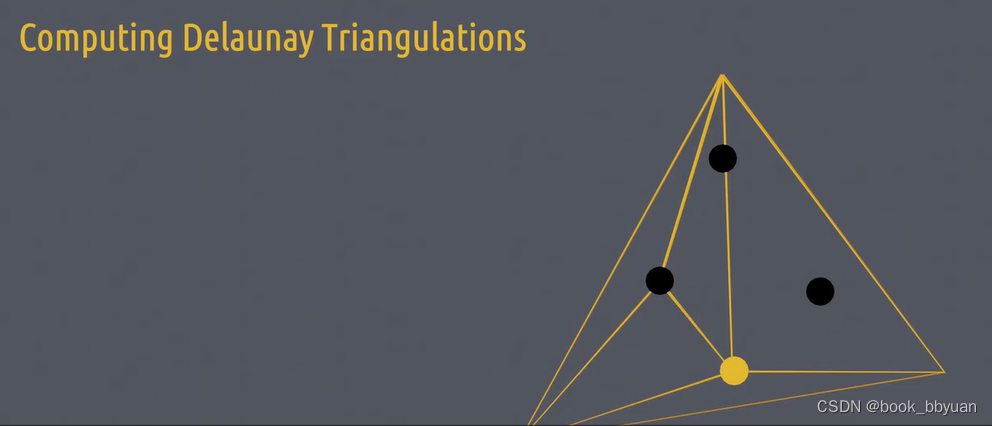
右侧这个点也要相同处理，有两个三角形的外接圆包含它

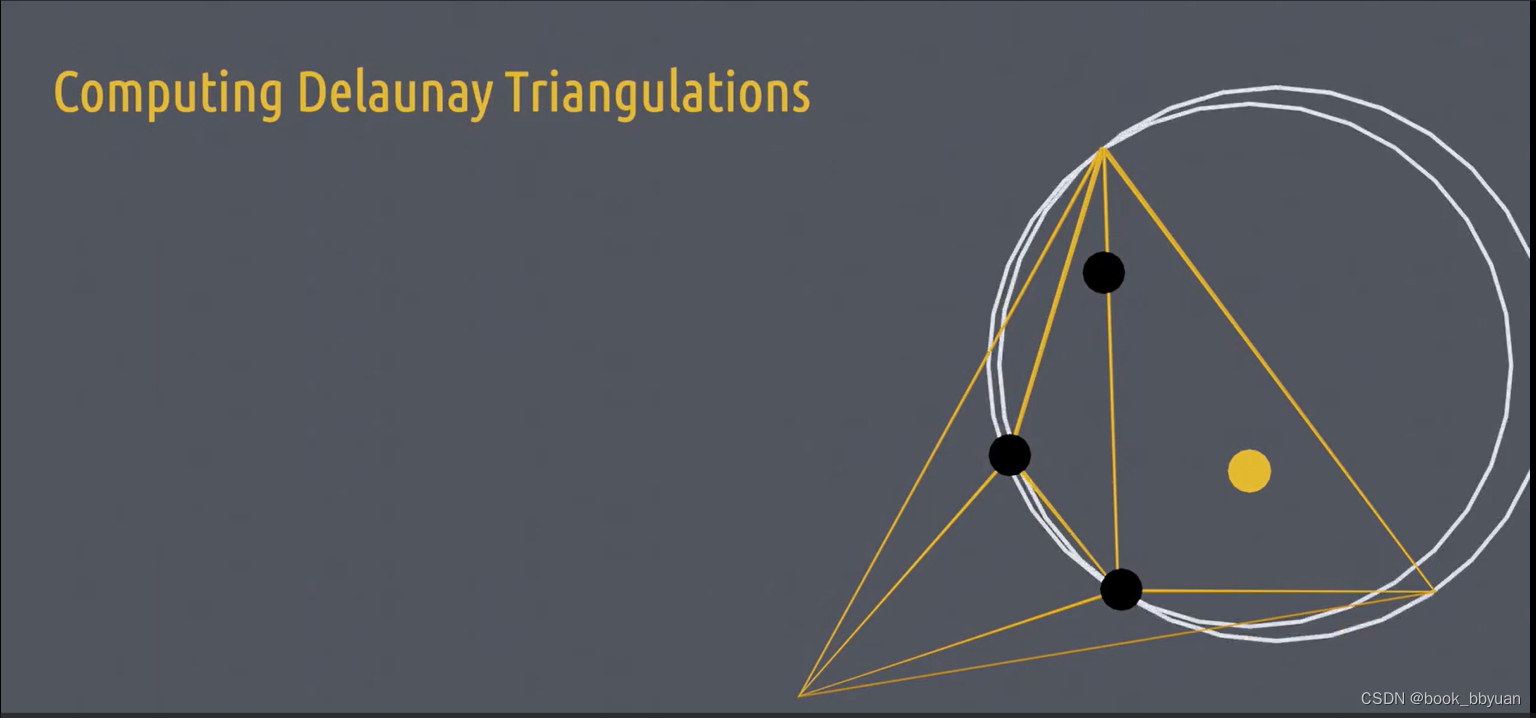
删掉公共边，形成星形多边形，把这个点和多边形的顶点连接起来

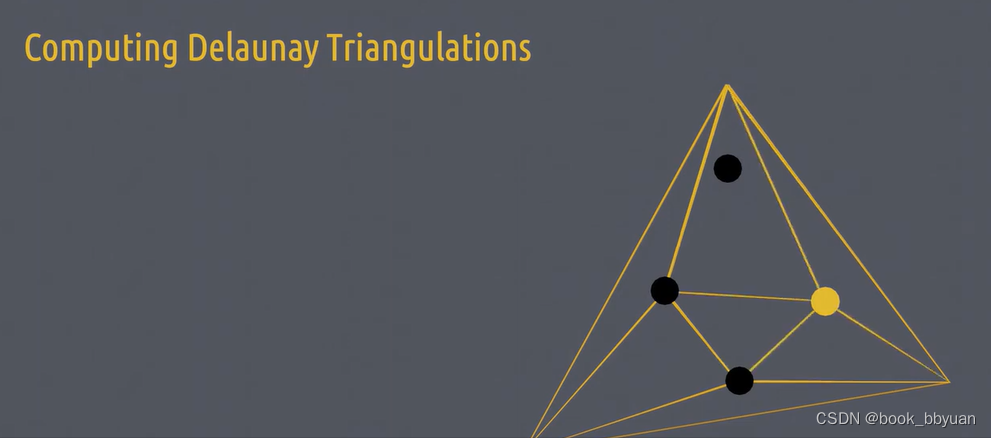
最后是最上面的点，也做相同的处理。

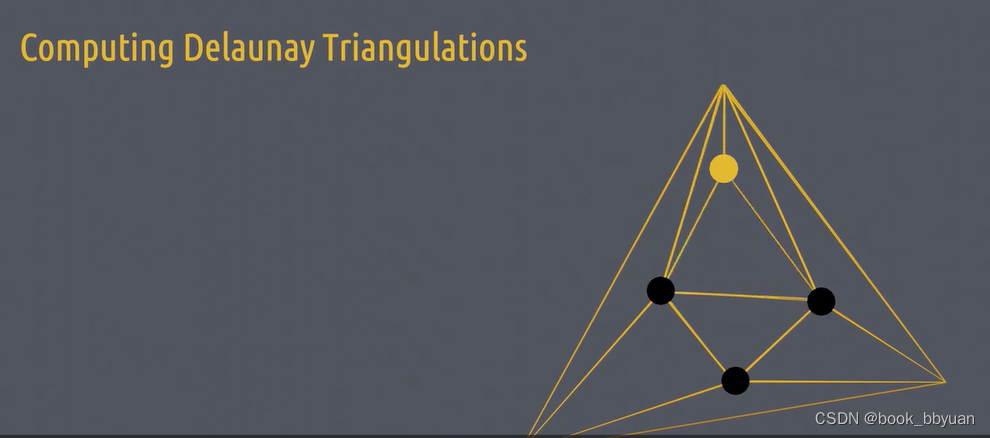
删掉 超三角形的边和顶点，那么那些连接线也得删掉，剩下就是我们要的得劳内三角剖分了

四、核心代码

triangles{1} = super_triangle;

for i = 1:length(points)
    point = points(i);
    triangles = AddPointToMesh(point, triangles);    
end

triangles = RemoveSuperTriangle(triangles, super_triangle);

mesh = triangles;

其中 AddpointToMesh

function good_triangles = AddPointToMesh(point,triangles)
    global Edge Circum_cricle Triangle
    k1 = 1;k2 =1;
    for i = 1:length(triangles)
        triangle = triangles{i};
        
%         plot_triangle(triangle);
%         plot_circumcircle(triangle);
        
        if IsInCircumCircle(point,triangle)
            edges{k1} = triangle.edges(1);
            edges{k1+1} = triangle.edges(2);
            edges{k1+2} = triangle.edges(3);
            k1 = k1+3;
        else
            good_triangles{k2} = triangle;
            k2 = k2+1;
        end
    end
    
    edges = GetUniqueEdges(edges);
    
    for i  = 1:length(edges)
        edge = edges{i};        
        e1 = Edge;        e2 = Edge;        e3 = Edge;        
        e1.points(1) = edge.points(1);
        e1.points(2) = edge.points(2);
        e2.points(1) = edge.points(2);
        e2.points(2) = point;
        e3.points(1) = point;
        e3.points(2) = edge.points(1);
        triangle = Triangle;
        triangle.edges(1) = e1;
        triangle.edges(2) = e2;
        triangle.edges(3) = e3;
        
        good_triangles{k2} = triangle;
%         plot_triangle(triangle);
        k2 = k2+ 1;
    end
    
end

 RemoveSuperTriangle

function mesh_triangles = RemoveSuperTriangle(triangles,super_triangle)
    super_tri_p1 = super_triangle.edges(1).points(1);
    super_tri_p2 = super_triangle.edges(2).points(1);
    super_tri_p3 = super_triangle.edges(3).points(1);
    k = 1;
    for i = 1:length(triangles)
        triangle = triangles{i};
        p1 = triangle.edges(1).points(1);
        p2 = triangle.edges(2).points(1);
        p3 = triangle.edges(3).points(1);
        
        if ~ ( is_point_same(p1,super_tri_p1) || is_point_same(p1 ,super_tri_p2) || is_point_same(p1, super_tri_p3) || ...
                    is_point_same(p2 ,super_tri_p1) || is_point_same(p2,super_tri_p2) || is_point_same(p2,super_tri_p3) || ...
                    is_point_same(p3, super_tri_p1) || is_point_same(p3,super_tri_p2) || is_point_same(p3, super_tri_p3))
            mesh_triangles{k} = triangle;
            k = k +1;
        end
    end
end

五、对比matlab自带函数和我们的算法：

        对比如下：自带函数

T = delaunay(x,y);
% tri = delaunayTriangulation(T, x, y ,z);

trisurf(T,x,y,z)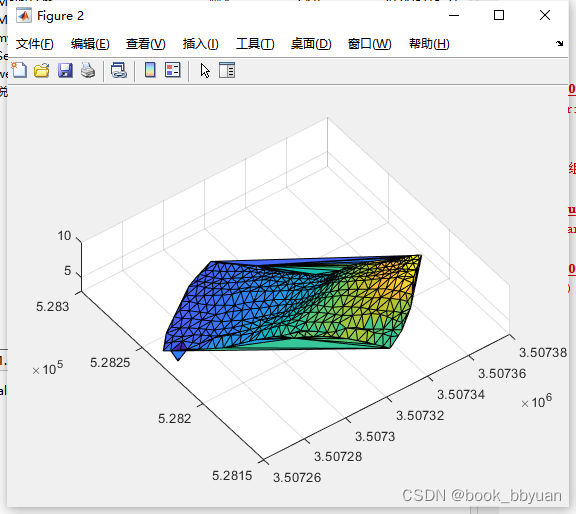

使用我们自己的

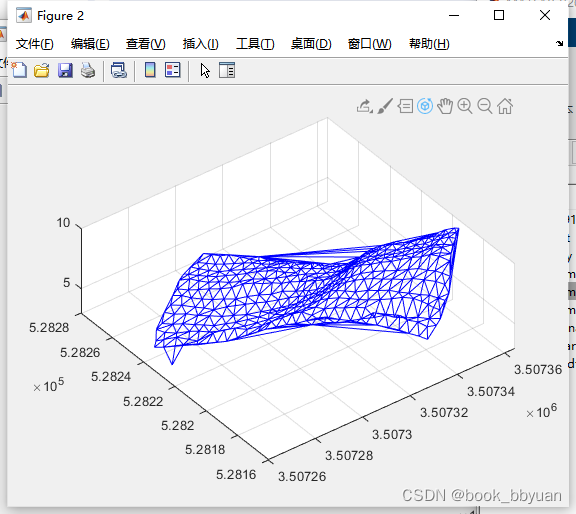
已经完全对上了

总结

完整的包可以从这里下载：

自定义函数实现delaunayTriangulation使用Bowyer-Watson算法资源-CSDN文库