【C++】学习笔记——二叉搜索树

news2024/10/5 21:16:02

文章目录

  • 十四、二叉搜索树
    • 1. 二叉搜索树的概念
    • 2. 二叉搜索树的实现
      • 查找
      • 插入
      • 中序遍历
      • 删除
      • 拷贝构造
      • 析构函数
      • 赋值重载
      • 完整代码
    • 3. 二叉搜索树的应用
      • K搜索模型
      • KV搜索模型
  • 未完待续

十四、二叉搜索树

1. 二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值。
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值。
它的左右子树也分别为二叉搜索树。

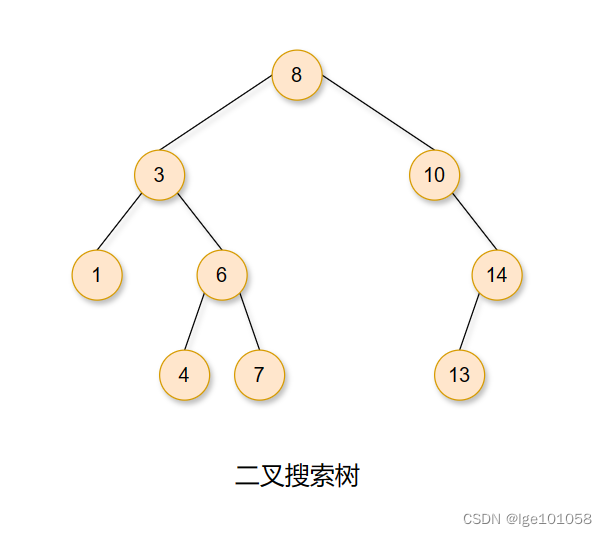
在这里插入图片描述

二叉搜索树的查找非常方便，最多查找 树的高度 次就能找到，他还有一个隐藏特点：二叉搜索树的中序遍历是有序的。

2. 二叉搜索树的实现

二叉搜索树，树是一种结构，需要用类来定义，节点也是一种结构，需要另一个类来定义。节点对数来说是完全公开的，所以节点我们使用 struct 。我们创建一个头文件：BinarySearchTree.h ，在里面先编写一个框架出来：

#pragma once

// struct BinarySearchTreeNode
// 节点结构体
template<class K>
struct BSTreeNode // 采用缩写
{
	typedef BSTreeNode<K> Node;

	// 指向左孩子的指针
	Node* _left;
	// 指向右孩子的指针
	Node* _right;
	// 关键字（存储的数据）
	K _key;

	BSTreeNode(const K& key)
	:_left(nullptr)
	,_right(nullptr)
	,_key(key)
{}
};

//class BinarySearchTree
// 二叉搜索树类
template<class K>
class BSTree // 采用缩写
{
	typedef BSTreeNode<K> Node;
public:
	//
private:
	Node* _root = nullptr;
};

查找

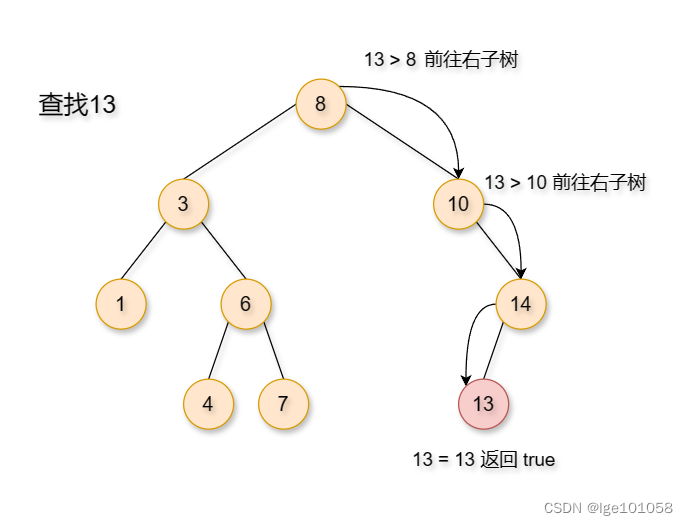
二叉搜索树非常适合查找，逻辑也非常简单。通过不断与当前节点比较而选择进入左子树或者右子树。

bool Find(const K& key)
{
	Node* cur = _root;

	// cur处有节点
	while (cur)
	{
		// 要查找的值比当前节点的值要小
		if (key < cur->_key)
		{
			// 前往左子树
			cur = cur->_left;
		}
		//要查找的值比当前节点的值要大
		else if (key > cur->_key)
		{
			// 前往右子树
			cur = cur->_right;
		}
		// 相等时
		else
		{
			return true;
		}
	}
	// 没找到
	return false;
}

在这里插入图片描述

插入

插入也是比较简单的，当插入的关键字已存在时，现阶段没有多大用处，我们就插入已有的关键字，当关键字不存在时，也是一种查找，当 找到空位置 时，该位置就可以插入。唯一需要注意的是，需要使用一个指针指向插入位置的父节点，否则无法进行节点之间的连接。

bool Insert(const K& key)
{
	// 注意空树
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}

	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (key < cur->_key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (key > cur->_key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			// 现阶段不插入相同的值
			return false;
		}
	}

	// 创建新节点
	cur = new Node(key);
	if (key < parent->_key)
	{
		// 新节点插在左子树
		parent->_left = cur;
	}
	else
	{
		// 新节点插在右子树
		parent->_right = cur;
	}

	return true;
}

中序遍历

中序遍历需要借助当前节点，所以需要一个形参，但是根节点又是属于类的私有成员变量，在外部无法访问，所以我们需要嵌套一层函数来访问。

// private内
void _InOrder(Node* root)
{
	if (root == nullptr)
	{
		return;
	}

	_InOrder(root->_left);
	std::cout << root->_key << " ";
	_InOrder(root->_right);
}

// 套一层函数来获取根节点
// public内
void InOrder()
{
	_InOrder(_root);
	std::cout << std::endl;
}

我们来测试一下：创建一个源文件 Test.cpp。

#include <iostream>
#include "BinarySearchTree.h"
using namespace std;

int main(void)
{
	BSTree<int> t;
	int a[] = { 8,3,1,10,6,4,7,14,13 };
	for (auto e : a)
	{
		t.Insert(e);
	}
	t.InOrder();
	return 0;
}

在这里插入图片描述
二叉搜索树的中序遍历确实是有序的，看来前面的函数都没有问题。

删除

前面的函数其实都是比较简单的，二叉搜索树的删除会比较困难。二叉搜索树的删除分为三种情况：

  1. 删除没有孩子节点的节点。
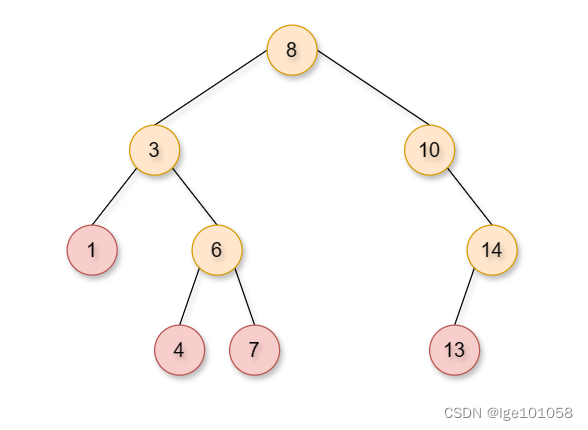
    在这里插入图片描述
    比如删除上图中的 1 4 7 13 。这种情况最简单，直接删掉即可。
  2. 删除只有一个孩子的节点。
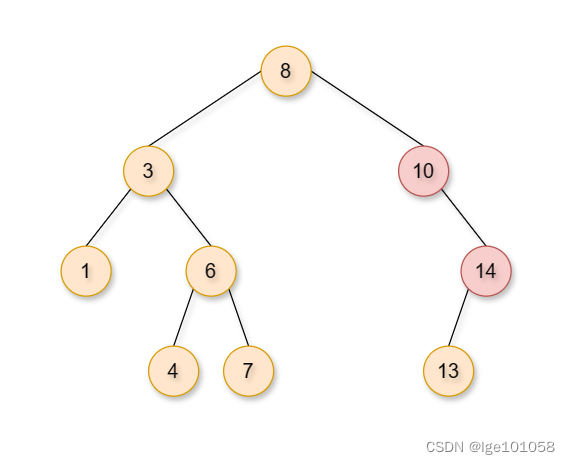
    在这里插入图片描述
    如上图中的 10 14 。这种情况也算是比较简单的，比如说我们要删除 14 。我们只需要将 14 的孩子 托付给 14 的父节点 即可。
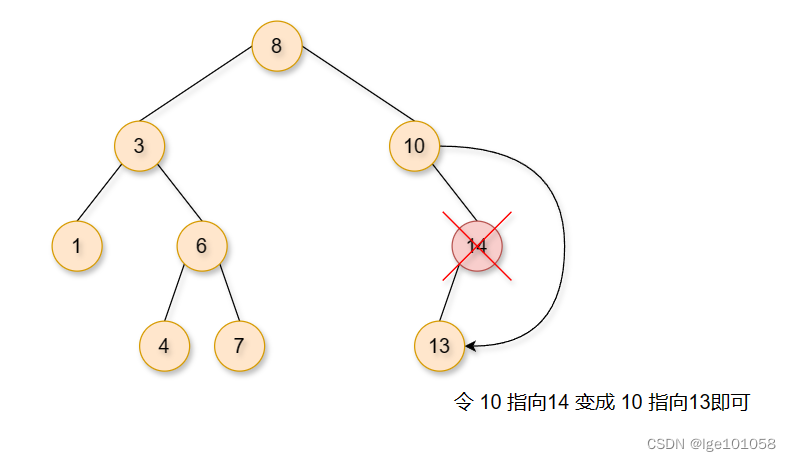
    在这里插入图片描述
  3. 删除有两个孩子的节点。


比如删除上图中的 8 3 6 。这种情况最为复杂，也最难。这种情况该怎么删除呢？有一种方法叫做 替换删除法 ，比如说我要删除 3 ，我可以从 3 的孩子里找出能够替换掉 3 的节点，即 左子树中的最右侧（最大）的节点，或者右子树中的最左侧（最小）的节点 。这两个节点与被删除的节点替换都可以完成删除操作。
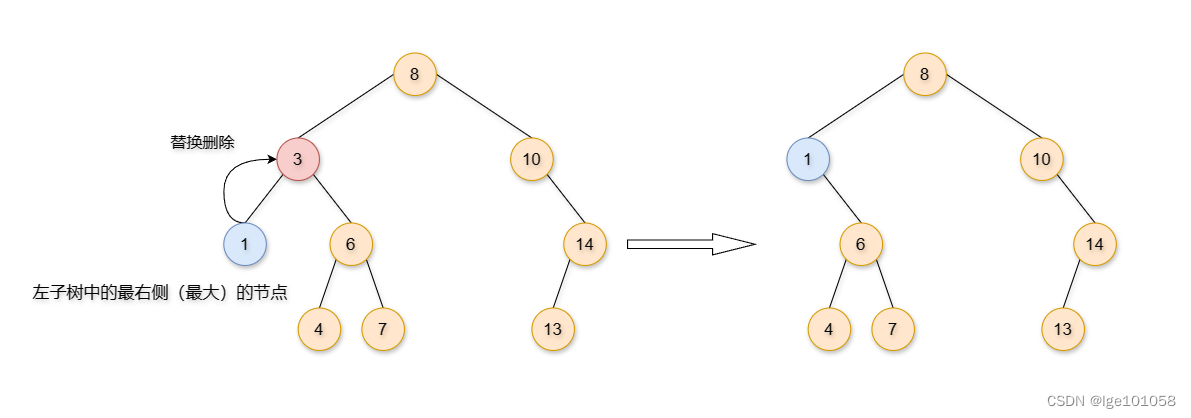
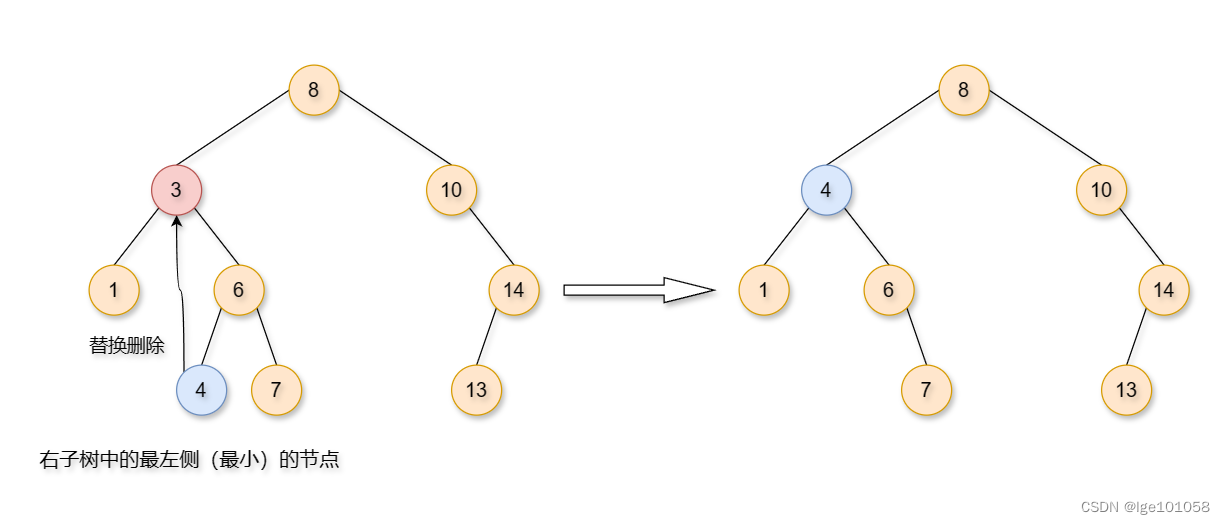
在这里插入图片描述

在这里插入图片描述

其实情况1和情况2差不多，因为情况1同样可以理解为将 空托付给父节点 。

bool Erase(const K& key)
{
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (key < cur->_key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (key > cur->_key)
		{
			parent = cur;
			cur = cur->_right;
		}
		// 找到了要删除的节点
		else
		{
			// 左子树为空，托付右子树
			if (cur->_left == nullptr)
			{
				if (cur == parent->_left)
				{
					parent->_left = cur->_right;
				}
				else
				{
					parent->_right = cur->_right;
				}
				delete cur;
				return true;
			}
			// 右子树为空，托付左子树
			else if (cur->_right == nullptr)
			{
				if (cur == parent->_left)
				{
					parent->_left = cur->_left;
				}
				else
				{
					parent->_right = cur->_left;
				}
				delete cur;
				return true;
			}
			// 都不为空使用替换删除法
			else
			{
				// 这里采用的是 找右子树的最小节点
				Node* rightMinParent = cur;
				Node* rightMin = cur->_right;
				while (rightMin->_left)
				{
					rightMinParent = rightMin;
					rightMin = rightMin->_left;
				}
				// 赋值
				cur->_key = rightMin->_key;
				// 托付
				if (rightMin == rightMinParent->_left)
				{
					rightMinParent->_left = rightMin->_right;
				}
				else
				{
					rightMinParent->_right = rightMin->_right;
				}

				delete rightMin;
				return true;
			}
		}
	}

	return false;
}

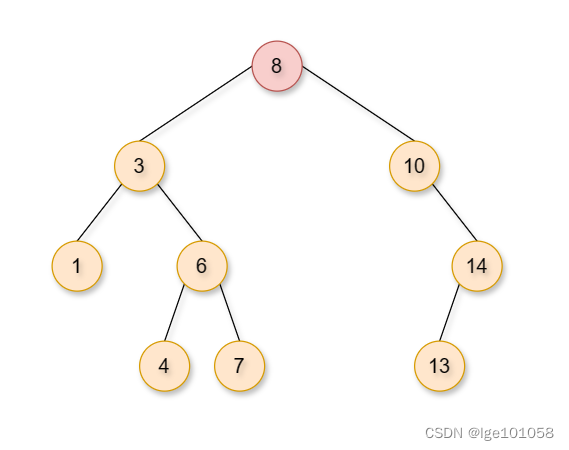
上面的函数有两个小细节，①假如删除8，则其右孩子 10 就是要删除的节点，所以 rightMinParent 不能初始化为 nullptr。②假如删除8，则其右孩子 10 就是要删除的节点，此时 10 是 8 的右节点，所以 rightMin 不一定是 rightMinParent 的左节点。
测试一下：

#include <iostream>
#include "BinarySearchTree.h"
using namespace std;

int main(void)
{
	BSTree<int> t;
	int a[] = { 8,3,1,10,6,4,7,14,13 };
	for (auto e : a)
	{
		t.Insert(e);
	}
	t.InOrder();
	t.Erase(8);
	t.InOrder();
	return 0;
}

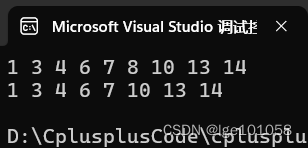
在这里插入图片描述
已经没有问题了吗？NoNoNo，当要删除的节点是根节点，并且只有左子树或者只有右子树时就会出问题了。此时 Parent 为 nullptr 但是被解引用了，所以我们需要加一下判断：

bool Erase(const K& key)
{
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (key < cur->_key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (key > cur->_key)
		{
			parent = cur;
			cur = cur->_right;
		}
		// 找到了要删除的节点
		else
		{
			// 左子树为空，托付右子树
			if (cur->_left == nullptr)
			{
				if (cur == _root)
				{
					_root = cur->_right;
				}
				else
				{
					if (cur == parent->_left)
					{
						parent->_left = cur->_right;
					}
					else
					{
						parent->_right = cur->_right;
					}
				}

				delete cur;
				return true;
			}
			// 右子树为空，托付左子树
			else if (cur->_right == nullptr)
			{
				if (cur == _root)
				{
					_root = cur->_left;
				}
				else
				{
					if (cur == parent->_left)
					{
						parent->_left = cur->_left;
					}
					else
					{
						parent->_right = cur->_left;
					}
				}

				delete cur;
				return true;
			}
			// 都不为空使用替换删除法
			else
			{
				// 这里采用的是 找右子树的最小节点
				Node* rightMinParent = cur;
				Node* rightMin = cur->_right;
				while (rightMin->_left)
				{
					rightMinParent = rightMin;
					rightMin = rightMin->_left;
				}
				// 赋值
				cur->_key = rightMin->_key;
				// 托付
				if (rightMin == rightMinParent->_left)
				{
					rightMinParent->_left = rightMin->_right;
				}
				else
				{
					rightMinParent->_right = rightMin->_right;
				}

				delete rightMin;
				return true;
			}
		}
	}

	return false;
}

拷贝构造

由于默认生成的拷贝构造函数是浅拷贝，直接拷贝构造会导致两个对象指向同一个二叉搜索树，我们要实现深拷贝所以要手动写一个拷贝构造函数。

// 强制生成默认构造函数
BSTree() = default;

// 拷贝构造函数
BSTree(const BSTree<K>& t)
{
	_root = Copy(t._root);
}

// private内
Node* Copy(Node* root)
{
	if (root == nullptr)
	{
		return nullptr;
	}

	Node* newRoot = new Node(root->_key);
	newRoot->_left = Copy(root->_left);
	newRoot->_right = Copy(root->_right);
	return newRoot;
}

析构函数

~BSTree()
{
	Destroy(_root);
}

// private内
void Destroy(Node* root)
{
	if (root == nullptr)
	{
		return;
	}

	Destroy(root->_left);
	Destroy(root->_right);
	delete root;
}

测试一下：

#include <iostream>
#include "BinarySearchTree.h"
using namespace std;

int main(void)
{
	BSTree<int> t;
	int a[] = { 8,3,1,10,6,4,7,14,13 };
	for (auto e : a)
	{
		t.Insert(e);
	}
	t.InOrder();
	BSTree<int> t1(t);
	t1.InOrder();
	return 0;
}

在这里插入图片描述

赋值重载

BSTree<K>& operator=(BSTree<K> t)
{
	std::swap(_root, t._root);
	return *this;
}

完整代码

#pragma once

// struct BinarySearchTreeNode
template<class K>
struct BSTreeNode
{
	typedef BSTreeNode<K> Node;

	// 指向左孩子的指针
	Node* _left;
	// 指向右孩子的指针
	Node* _right;
	// 关键字（存储的数据）
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
};

//class BinarySearchTree
template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	// 强制生成默认构造函数
	BSTree() = default;

	// 拷贝构造函数
	BSTree(const BSTree<K>& t)
	{
		_root = Copy(t._root);
	}

	BSTree<K>& operator=(BSTree<K> t)
	{
		std::swap(_root, t._root);
		return *this;
	}

	// 析构函数
	~BSTree()
	{
		Destroy(_root);
	}

	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				// 现阶段不插入相同的值
				return false;
			}
		}

		// 创建新节点
		cur = new Node(key);
		if (key < parent->_key)
		{
			// 新节点插在左子树
			parent->_left = cur;
		}
		else
		{
			// 新节点插在右子树
			parent->_right = cur;
		}

		return true;
	}

	bool Find(const K& key)
	{
		Node* cur = _root;

		// cur处有节点
		while (cur)
		{
			// 要查找的值比当前节点的值要小
			if (key < cur->_key)
			{
				// 前往左子树
				cur = cur->_left;
			}
			//要查找的值比当前节点的值要大
			else if (key > cur->_key)
			{
				// 前往右子树
				cur = cur->_right;
			}
			// 相等时
			else
			{
				return true;
			}
		}
		// 没找到
		return false;
	}

	void InOrder()
	{
		_InOrder(_root);
		std::cout << std::endl;
	}

	bool Erase(const K& key)
	{
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			// 找到了要删除的节点
			else
			{
				// 左子树为空，托付右子树
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}

					delete cur;
					return true;
				}
				// 右子树为空，托付左子树
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}

					delete cur;
					return true;
				}
				// 都不为空使用替换删除法
				else
				{
					// 这里采用的是 找右子树的最小节点
					Node* rightMinParent = cur;
					Node* rightMin = cur->_right;
					while (rightMin->_left)
					{
						rightMinParent = rightMin;
						rightMin = rightMin->_left;
					}
					// 赋值
					cur->_key = rightMin->_key;
					// 托付
					if (rightMin == rightMinParent->_left)
					{
						rightMinParent->_left = rightMin->_right;
					}
					else
					{
						rightMinParent->_right = rightMin->_right;
					}

					delete rightMin;
					return true;
				}
			}
		}

		return false;
	}
private:
	Node* Copy(Node* root)
	{
		if (root == nullptr)
		{
			return nullptr;
		}

		Node* newRoot = new Node(root->_key);
		newRoot->_left = Copy(root->_left);
		newRoot->_right = Copy(root->_right);
		return newRoot;
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		std::cout << root->_key << " ";
		_InOrder(root->_right);
	}

	void Destroy(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		Destroy(root->_left);
		Destroy(root->_right);
		delete root;
	}

	Node* _root = nullptr;
};

3. 二叉搜索树的应用

K搜索模型

K搜索模型主要运用于想要 快速找到某个值在不在 。比如说门禁系统。

KV搜索模型

KV搜索模型主要运用于想要 通过某个值（key）查找另一个值（value）在不在 。比如说商场车库，通过车牌号找到进车库的时间好用来计费。

上面实现的就是 K搜索模型 ，如何实现 KV搜索模型 呢？其实也不难，节点结构体内多存入一个 value 即可，然后输入 key 的时候也要输入 value。逻辑与 K搜索模型 大差不差。

未完待续

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1684946.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

BUUCTF---misc---[MRCTF2020]ezmisc

BUUCTF---misc---[MRCTF2020]ezmisc

1、附件下载后是一张图片 2、查看属性&#xff0c;winhex分析&#xff0c;没发现什么 3、在kali中binwalk和foremost也没找到什么信息 4、用stegsolve分析也没发现什么 5、这里几乎常见的misc方法都试过了&#xff0c;还是没有发现什么 6、回归到图片本身&#xff0c;想到的…
阅读更多...
正心归一、绽放真我 好普集团正一生命文化艺术大赛（中老年赛区）正式启动

正心归一、绽放真我 好普集团正一生命文化艺术大赛（中老年赛区）正式启动

为进一步弘扬社会主义核心价值观&#xff0c;弘扬生命文化&#xff0c;提升公众对生命价值的认识与尊重&#xff0c;同时展现中老年艺术家的创作才华&#xff0c;激发广大中老年朋友的艺术热情和创造力。好普集团主办&#xff0c;幸福金龄会与正一生命科学研究&#xff08;广州…
阅读更多...
CSS单行、同行文本左右对齐

CSS单行、同行文本左右对齐

再项目需求中&#xff0c;UI小姐姐常常要考虑项目的排版样式更简洁高级&#xff0c;常常会在项目设置内容或者字体两端对齐的效果&#xff0c;比如&#xff0c;在做表单时我们经常遇到让上下两个字段对齐的情况&#xff0c;比如姓名&#xff0c; 手机号码&#xff0c; 出生地等…
阅读更多...
分布式音乐播放器适配了Stage模型

分布式音乐播放器适配了Stage模型

OpenAtom OpenHarmony&#xff08;以下简称“OpenHarmony”&#xff09;应用开发自API 8及其更早版本一直使用的是FA模型进行开发。FA模型是Feature Ability的缩写&#xff0c;它和PA&#xff08;Particle Ability&#xff09;两种类型是过往长期推广的术语&#xff0c;深入人心…
阅读更多...
flannel详细介绍

flannel详细介绍

一、前言 Flannel 是一个简单、高效的容器网络解决方案&#xff0c;适用于需要在多个主机上运行容器的场景。它通过虚拟网络技术和 IP 地址管理来实现容器之间的通信和跨主机连接&#xff0c;为容器平台提供了可靠的网络基础设施&#xff0c;flannel有三种模式&#xff0c;分别…
阅读更多...
【OceanBase诊断调优】—— 直连普通租户时遇到报错：Tenant not in this server

【OceanBase诊断调优】—— 直连普通租户时遇到报错：Tenant not in this server

本文介绍了直连 OceanBase 数据库中的普通租户时&#xff0c;出现报错&#xff1a;ERROR 5150 (HY000) : Tenant not in this server 的处理方法。 问题描述 在 n-n 或者 n-n-n (n>1) 的部署架构中&#xff0c;使用 2881 端口 直连 OceanBase 集群的普通租户&#xff0c;可…
阅读更多...
Vue2基础及其进阶面试（一）

Vue2基础及其进阶面试（一）

简单版项目初始化 新建一个vue2 官网文档&#xff1a;介绍 — Vue.js 先确保下载了vue的脚手架 npm install -g vue-cli npm install -g vue/cli --force vue -V 创建项目 vue create 自己起个名字 选择自己选择特性 选择&#xff1a; Babel&#xff1a;他可以将我们写…
阅读更多...
华院计算 | 简单而复杂的“生命游戏”

华院计算 | 简单而复杂的“生命游戏”

人类是社会动物&#xff0c;而人类的社会活动则既简单又复杂。长期以来&#xff0c;数学家、计算机科学家和社会学家们一直试图用简单明了的方式方法去刻画错综复杂的社会现象&#xff0c;其中“生命游戏”提供了一个“寓科学于娱乐”的活动框架。 【一】导引 让我们先来玩一…
阅读更多...
接口自动化测试Requests库实战超细详解

接口自动化测试Requests库实战超细详解

一、requests库 Requests is an elegant and simple HTTP library for Python, built for human beings. Requests库就是一个使用Python语言发送HTTP请求的一个类库。 github地址&#xff1a;GitHub - psf/requests: A simple, yet elegant, HTTP library. 中文地址&#xff…
阅读更多...
【华为】将eNSP导入CRT，并解决不能敲Tab问题

【华为】将eNSP导入CRT，并解决不能敲Tab问题

华为】将eNSP导入CRT&#xff0c;并解决不能敲Tab问题 eNSP导入CRT打开eNSP&#xff0c;新建一个拓扑右键启动查看串口号关联CRT成功界面 SecureCRT连接华为模拟器ensp,Tab键不能补全问题选择Options&#xff08;选项&#xff09;-- Global Options &#xff08;全局选项&#…
阅读更多...
民国漫画杂志《时代漫画》第6期.PDF

民国漫画杂志《时代漫画》第6期.PDF

时代漫画06.PDF: https://url03.ctfile.com/f/1779803-1247397790-72c351?p9586 (访问密码: 9586) 《时代漫画》的杂志在1934年诞生了&#xff0c;截止1937年6月战争来临被迫停刊共发行了39期。 ps:资源来源网络&#xff01;
阅读更多...
MySQL慢查询原因总结

MySQL慢查询原因总结

文章目录 一.SQL没加索引二. SQL 索引不生效2.1 隐式的类型转换&#xff0c;索引失效2.2 查询条件包含or&#xff0c;可能导致索引失效2.3 like通配符可能导致索引失效2.4 查询条件不满足联合索引的最左匹配原则2.5 在索引列上使用mysql的内置函数2.6 对索引进行列运算&#xf…
阅读更多...
低耦合双写一致性方案-使用canal+MQ

低耦合双写一致性方案-使用canal+MQ

需求&#xff1a;继上一篇使用xxljob实现数据的全量同步到es后&#xff0c;当数据库中新增、删除、修改数据时&#xff0c;应该对es中的对应索引库实现增量同步。 本文介绍了2种双写一致性方案&#xff0c;对其中使用MQ的方案进行了实现。 1. 方案设计 1.1 数据一致性问题分析…
阅读更多...
QT7_视频知识点笔记_5_线程，数据库

QT7_视频知识点笔记_5_线程，数据库

多线程 两种办法&#xff1a;第一种&#xff1a;Qt4.7之前的线程使用的方法&#xff08;简单&#xff09;&#xff1b;第二种&#xff1a;Qt4.7之后的&#xff08;灵活–推荐&#xff09;----connect最后一个参数的作用&#xff1a;默认连接&#xff0c;队列连接&#xff0c;直…
阅读更多...
vue3使用mitt.js进行各种组件间通信

vue3使用mitt.js进行各种组件间通信

我们在vue工程中&#xff0c;除开vue自带的什么父子间&#xff0c;祖孙间通信&#xff0c;还有一个非常方便的通信方式&#xff0c;类似Vue2.x 使用 EventBus 进行组件通信&#xff0c;而 Vue3.x 推荐使用 mitt.js。可以实现各个组件间的通信 优点&#xff1a;首先它足够小&…
阅读更多...
从业务角度来看，DevOps 是什么？

从业务角度来看，DevOps 是什么？

如果您在我们的应用程序名称中看到“DevOps”&#xff0c;这意味着我们必须正确解释该术语&#xff0c;我们会这样做&#xff0c;但角度会有所不同。让我们从业务角度看看 DevOps 是什么。 通用名称 首先你应该知道&#xff0c;DevOps 没有明确的定义。是的。 大多数情况下&a…
阅读更多...
分类和品牌关联

分类和品牌关联

文章目录 1.数据库表设计1.多表关联设计2.创建表 2.使用renren-generator生成CRUD1.基本配置检查1.generator.properties2.application.yml 2.生成代码1.进入localhost:81生成代码2.将main目录覆盖sunliving-commodity模块的main目录 3.代码检查1.注释掉CategoryBrandRelationC…
阅读更多...
使用xsd验证xml格式的正确性

使用xsd验证xml格式的正确性

1.1 基础知识介绍 XML简介&#xff1a;XML是可扩展标记语言&#xff08;eXtensible Markup Language&#xff09;的缩写&#xff0c;它是一种数据表示格式&#xff0c;可以描述非常复杂的数据结构&#xff0c;常用于传输和存储数据。xml文件、xml消息。XSD简介&#xff1a;是X…
阅读更多...
JS对象超细

JS对象超细

目录 一、对象是什么 1.对象声明语法 2.对象有属性和方法组成 二、对象的使用 1.对象的使用 &#xff08;1&#xff09;查 &#xff08;2&#xff09;改 &#xff08;3&#xff09;增 &#xff08;4&#xff09;删&#xff08;了解&#xff09; &#xff08;5&#xf…
阅读更多...
九州未来十二周年丨聚力同行，奔赴智能新未来

九州未来十二周年丨聚力同行，奔赴智能新未来

九州未来迎来十二周年&#xff01; 从国内首批提供 OpenStack 云服务的专业公司&#xff0c; 经过十二年的发展&#xff0c; 现今成长为开放智能云边架构引领者。 在这十二年的时间中&#xff0c; 九州未来持续创新&#xff0c;步履不停&#xff0c; 打造成熟的云基础设施…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023