大家好,层次分析法(Analytic Hierarchy Process,AHP)是一种多准则决策方法,它帮助决策者处理复杂的决策问题,将其分解成层次结构,然后通过两两比较来确定各个层次的因素之间的相对重要性。这种分析方式允许决策者对问题进行系统化的、结构化的处理,从而更清晰地理解各因素之间的相互关系和作用。
AHP的核心思想是通过对各个因素的两两比较,得出一个比较矩阵,然后利用特定的数学方法(如特征值分解)计算出每个因素的权重,最终将这些权重综合起来,确定备选方案的总排序。在这个过程中,决策者需要结合专业知识和主观判断来进行比较和权衡,从而达到对问题的全面分析和综合评价的目的。
层次分析法(AHP)体现了分解问题、判断因素重要性和综合评价的思维特征,使得决策者能够更系统、更科学地进行决策分析,提高了决策的准确性和可信度。
1.层次分析法评价决策
运用层次分析法进行评价或决策的流程如下:
-
建立递阶层次结构: 首先,需要将复杂的评价系统或决策问题分解成一系列逐层细化的要素。这些要素从总体到细节依次排列,形成一个递阶结构,以反映问题的层次性质和要素之间的关系。
-
两两比较及一致性检验: 对于同一层次中的各元素,进行两两比较,评价它们对上一层次中某一准则的重要性。这些比较通常通过专家判断或者调查问卷来完成。比较的结果构成了一个判断矩阵。然后,进行一致性检验,以确保专家的判断具有一定的稳定性和逻辑性。
-
计算相对权重: 通过对判断矩阵进行数学处理,可以计算出每个要素对于所考虑准则的相对权重。这通常涉及特征值分解等数学方法,从而得出各要素的权重,以便后续的综合分析。
-
合成权重与排序: 最后,将各层要素对系统目的的相对权重进行合成,得出各备选方案的综合权重,并据此进行排序。这样就能够确定最优的决策方案或者评价结论。
通过这四个流程操作,层次分析法能够帮助决策者系统地分析复杂的问题,综合考虑各要素的重要性,从而做出更加科学和合理的决策。
2.层次分析法分析步骤
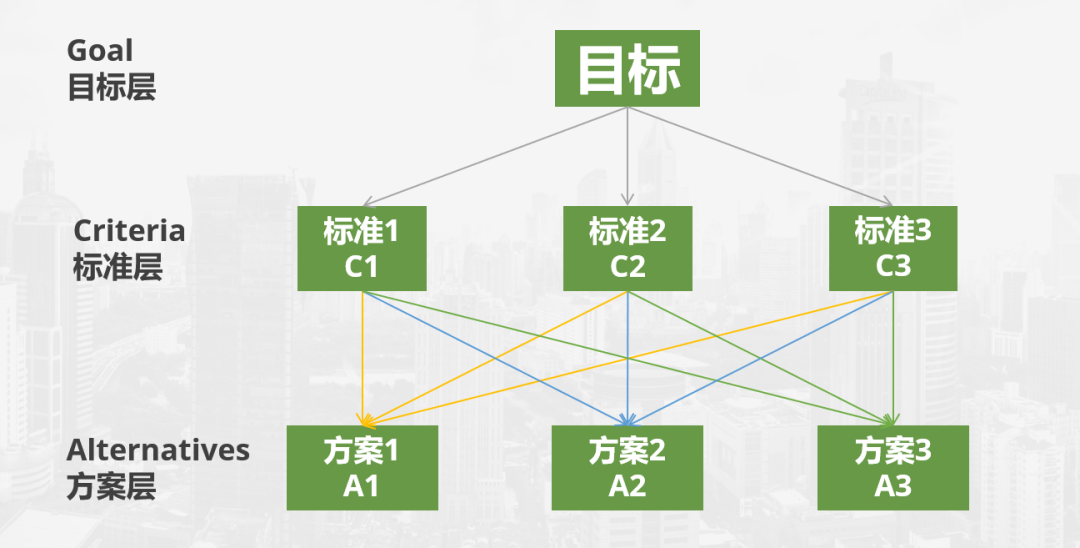
层次结构由以下几部分构成:
-
目标:通过提前制定SMART目标(具体的-可衡量的-可实现的-相关的-时限的),组织中的每个人都知道他们想要实现什么。
-
标准:通过确定实现目标所重要的标准,建立了一个框架。每个目标都有一定程度上重要的标准来实现它。通过设置标准,每个人在做出决策时都知道了要求。
-
候选方案:通过考虑候选方案及其优缺点、及评分,组织被引导到最佳的最终决策。
接下来,需要对标准层的各个方面进行主观经验打分,以确定评价尺度。例如,对标准层的C1到C5的重要性进行主观打分,根据以下原则进行评分:
-
1:两个要素相比具有同等重要性
-
3:两个要素相比,前者略微重要于后者
-
5:两个要素相比,前者明显重要于后者
-
7:两个要素相比,前者强烈重要于后者
-
9:两个要素相比,前者极端重要于后者
-
2、4、6、8:上述相邻判断的中间值
-
倒数:两个要素相比,后者重要性优于前者
C1到C5的重要性进行主观打分矩阵(模拟)及计算权重和归一化的权重:
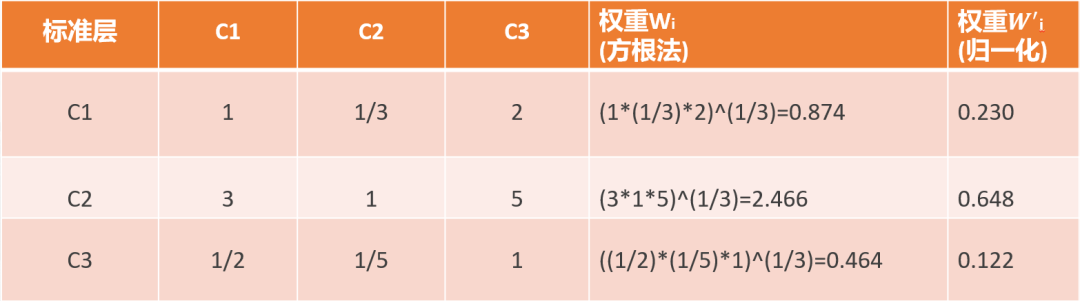
下面分别评价三个方案A1/A2/A3在不通同标准(C1/C2/C3)的评价矩阵和评分,算法同标准层:
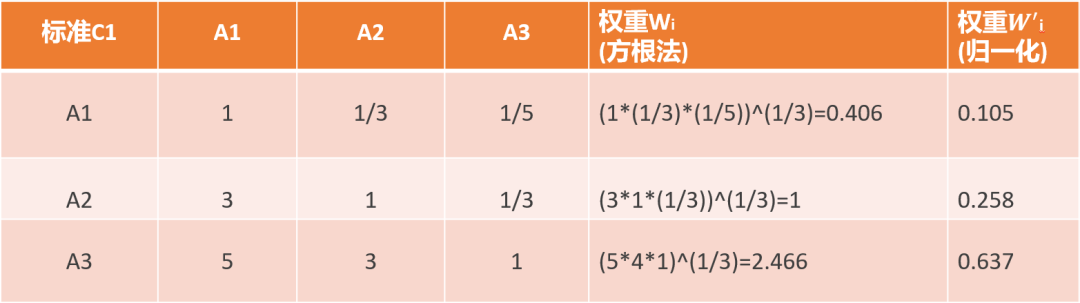
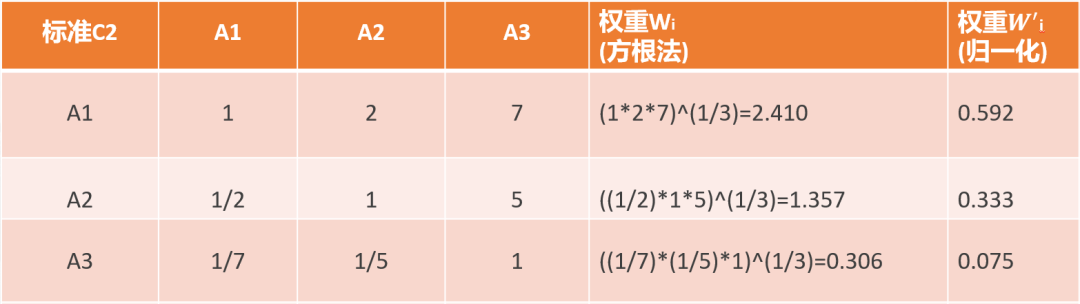
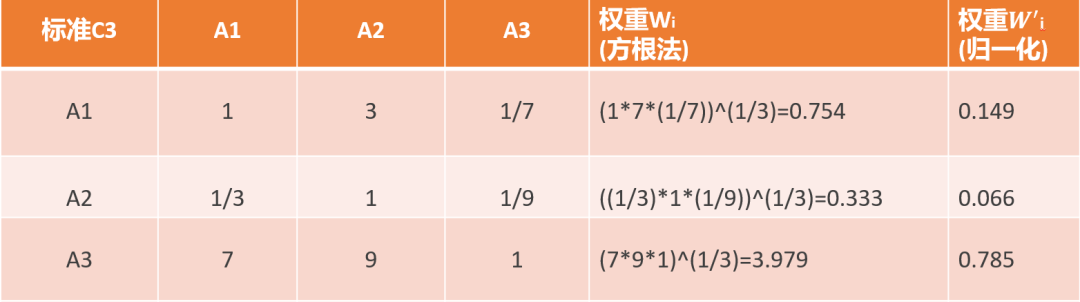
上面三张图是三个方案在各个标准上的评分,整个体系的评分如下图:
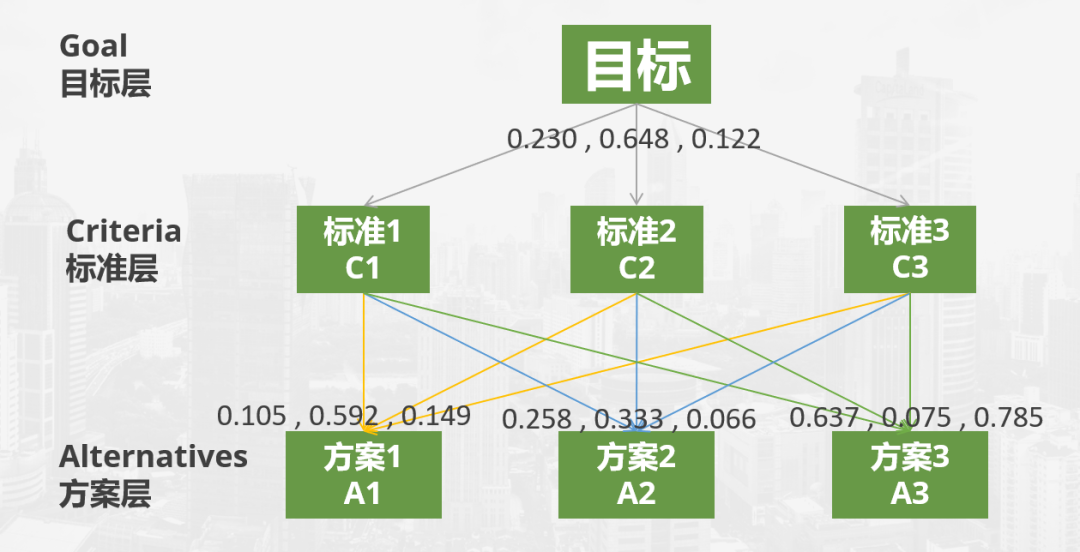
三个标准权重:C=[0.230,0.648,0.122]
A1的评分:A1=[0.105,0.592,0.149]
A2的评分:A1=[0.258,0.333,0.066]
A3的评分:A1=[0.637,0.075,0.785]
计算各个方案总评分并对方案进行排序:A1、A3、A2
方案A1:A1*C=[0.230,0.648,0.122]*[0.105,0.592,0.149]=0.426
方案A2:A2*C=[0.230,0.648,0.122]*[0.258,0.333,0.066]=0.283
方案A3:A3*C=[0.230,0.648,0.122]*[0.637,0.075,0.785]=0.291
import numpy as np
import pandas as pd
C=np.array([0.230,0.648,0.122])
A1=np.array([0.105,0.592,0.149]).T
A2=np.array([0.258,0.333,0.066]).T
A3=np.array([0.637,0.075,0.785]).T
print(f'方案A1 得分:%.3f' % C.dot(A1)) #矩阵相乘
print(f'方案A2 得分:%.3f' % C.dot(A2))
print(f'方案A3 得分:%.3f' % C.dot(A3))
3.智慧决策的利器
层次分析法(AHP)是组织进行决策的工具,允许在做出决定之前考虑某些因素(标准)。每个因素(标准)都可以根据其重要性来衡量。通过将数学值赋予相关人员的愿望,可以进行充分的比较。数值在决策过程的每个环节都发挥着重要作用。设定这些数值有助于所有相关人员基于数学证据做出选择。每个候选方案都会根据标准获得分数。这些因素在一个表格中进行权衡,其中也包括负面因素。运用数学逻辑,可以更轻松地做出明智的决策。
层次分析法(AHP)是组织进行决策的利器,通过考虑各种因素的重要性,帮助决策者做出明智的选择。通过数学化的方法,将愿望量化为数值,并结合权重计算,实现全面的评估。每个候选方案都经过标准的评分和权衡,以便更好地指导决策。AHP的运用使得复杂问题的分析和决策变得更加系统化和科学化,提高了决策的准确性和可信度。