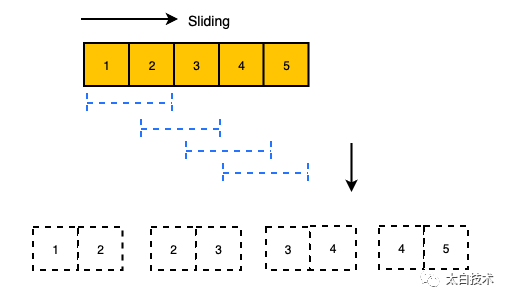
238.除自身以外各元素的乘积
给你一个整数数组nums,返回数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积。
题目数据保证数组nums之中任意元素的全部前缀元素和后缀的乘积都在32位整数范围内。
请不要使用除法,且在o(n)时间复杂度内完成此题。
示例 1:
输入: nums =[1,2,3,4]输出:[24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]
解题:
自身题解:超出时间限制
class Solution {
public int[] productExceptSelf(int[] nums) {
int len=nums.length;
int[] answer=new int[len];
for(int i=0;i<len;i++)
{
answer[i]= mult(nums,i);
}
return answer;
}
public int mult(int []nums,int i)
{
int multsum=1;
for(int j=0;j<nums.length;j++)
{
if(j!=i)
{
multsum*=nums[j];
}
}
return multsum;
}
}官方题解:
方法:左右乘积列表
思路我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
对于给定索引 i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法。
算法
初始化两个空数组 L 和 R。对于给定索引 i,L[i] 代表的是 i 左侧所有数字的乘积,R[i] 代表的是 i 右侧所有数字的乘积。
我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L,L[0] 应该是 1,因为第一个元素的左边没有元素。对于其他元素:L[i] = L[i-1] * nums[i-1]。
同理,对于数组 R,R[length-1] 应为 1。length 指的是输入数组的大小。其他元素:R[i] = R[i+1] * nums[i+1]。
当 R 和 L 数组填充完成,我们只需要在输入数组上迭代,且索引 i 处的值为:L[i] * R[i]。
class Solution {
public int[] productExceptSelf(int[] nums) {
int length = nums.length;
// L 和 R 分别表示左右两侧的乘积列表
int[] L = new int[length];
int[] R = new int[length];
int[] answer = new int[length];
// L[i] 为索引 i 左侧所有元素的乘积
// 对于索引为 '0' 的元素,因为左侧没有元素,所以 L[0] = 1
L[0] = 1;
for (int i = 1; i < length; i++) {
L[i] = nums[i - 1] * L[i - 1];
}
// R[i] 为索引 i 右侧所有元素的乘积
// 对于索引为 'length-1' 的元素,因为右侧没有元素,所以 R[length-1] = 1
R[length - 1] = 1;
for (int i = length - 2; i >= 0; i--) {
R[i] = nums[i + 1] * R[i + 1];
}
// 对于索引 i,除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
for (int i = 0; i < length; i++) {
answer[i] = L[i] * R[i];
}
return answer;
}
}134.加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2] 输出: 3 解释: 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油 开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油 开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油 开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油 开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。 因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3] 输出: -1 解释: 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。 我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油 开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油 开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油 你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。 因此,无论怎样,你都不可能绕环路行驶一周。
自己的解法:只正确一半
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
// 1.保证起始序号的gas>cost
// 2.保证每一个站台的剩余油量大于0
int len1=gas.length;
int len2=cost.length;
// 方案——依次遍历
int i=0;
int sum1=0;
int sum2=0;
int flag;
// gas[i]从i开始遍历的所有和的数组
for(int init=0;init<len1;init++)
{
flag=0;
for(i=init;i<len1+init;i++)
{
if(i<len1)
{
sum1+=gas[i];
sum2+=cost[i];
}
else
{
sum1+=gas[i-len1];
sum2+=cost[i-len1];
}
if(sum1<sum2)
{
flag=1;
break;
}
}
if(flag==0)
return init;
}
return -1;
}
}官方题解:
思路与算法
最容易想到的解法是:从头到尾遍历每个加油站,并检查以该加油站为起点,最终能否行驶一周。我们可以通过减小被检查的加油站数目,来降低总的时间复杂度。如果不能环绕一周,那么在失败的这个加油站之前的所有加油站至起始加油站都不行。因为在这之前汽车的油量一定是>0的。
那么下一次应该从失败的这一次加油站开始,大大减少时间,至此,算法应该很清楚了。
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int n = gas.length;
int i = 0;
while (i < n) {
int sumOfGas = 0, sumOfCost = 0;
// cnt 在这里将成功的加油站计数标记,便于下次直接跳转至失败的下一个元素。
int cnt = 0;
while (cnt < n) {
int j = (i + cnt) % n;
sumOfGas += gas[j];
sumOfCost += cost[j];
if (sumOfCost > sumOfGas) {
break;
}
cnt++;
}
// 如果成功了个加油站,就返回
if (cnt == n) {
return i;
// 否则返回失败的加油站的下一个
} else {
i = i + cnt + 1;
}
}
return -1;
}
}
总结:
1、一个成功,则之前的都成功,可以大幅减少时间。
2、凡是使用往返遍历的,使用 j = (i + cnt) % n;
135.分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2] 输出:5 解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
自己的题解:
思考的太简单了,就不放上来了,把一些精彩的部分放上来:
candys[i]=(ratings[i]>ratings[i-1])?(candys[i-1]+1):1;官方题解:


class Solution {
public int candy(int[] ratings) {
int n = ratings.length;
int[] left = new int[n];
for (int i = 0; i < n; i++) {
if (i > 0 && ratings[i] > ratings[i - 1]) {
left[i] = left[i - 1] + 1;
} else {
left[i] = 1;
}
}
int right = 0, ret = 0;
for (int i = n - 1; i >= 0; i--) {
if (i < n - 1 && ratings[i] > ratings[i + 1]) {
right++;
} else {
right = 1;
}
ret += Math.max(left[i], right);
}
return ret;
}
}
核心思想:
1、左右遍历分别满足两种规则,取最后在比较取最大值即可
13.罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。
示例 1:
输入: s = "III" 输出: 3
示例 2:
输入: s = "IV" 输出: 4
示例 3:
输入: s = "IX" 输出: 9
示例 4:
输入: s = "LVIII" 输出: 58 解释: L = 50, V= 5, III = 3.
示例 5:
输入: s = "MCMXCIV" 输出: 1994 解释: M = 1000, CM = 900, XC = 90, IV = 4.
class Solution {
Map<Character, Integer> symbolValues = new HashMap<Character, Integer>() {{
put('I', 1);
put('V', 5);
put('X', 10);
put('L', 50);
put('C', 100);
put('D', 500);
put('M', 1000);
}};
public int romanToInt(String s) {
int ans = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
int value = symbolValues.get(s.charAt(i));
if (i < n - 1 && value < symbolValues.get(s.charAt(i + 1))) {
ans -= value;
} else {
ans += value;
}
}
return ans;
}
}
//这里的 i < n - 1 主要是出于以下考虑:
//这是为了确保在判断当前字符与下一个字符的关系时,下一个字符是存在的。因为如果 i 已经是字符串的最后一个位置(即 i = n - 1),那么就不存在下一个字符了,此时再去比较就会导致数组越界错误。通过这样的条件限制,就可以只在有下一个字符可比较的情况下才进行相应的特殊处理(判断大小并做减或加的操作)。