1 背景

自18世纪中叶以来，由于快速城市化、人口增长和技术发展，导致一氧化二氮（N2O）、 甲烷（CH4）和二氧化碳（CO 2）等温室气体浓度急剧上升，引发了全球变暖、海平面上 升、极端天气以及环境污染等一系列问题，严重制约了社会、经济、生态的可持续发展， 威胁人类生存与健康[1]。

由于温室气体排放增加引起的全球变暖、极 端高温和热浪、龙卷风、飓风、干旱和洪水等自然灾害成为新常态，已经成为世界各国 政府和学术界关注的焦点[ 2]，因此，估算大气中CO2浓度是我们研究全球变暖等问题的 最可靠的方法，探讨CO2循环和碳源汇收支的变化规律是应对全球气候变化的关键所在。故本文针对巴西1960年-2014年固体燃料消耗产生的CO2排放量来进行分析和预测，针对特定的数据进行建模分析，最终得出相应的结论。

2 数据和方法说明

本文所运用到的数据是全球暖化数据集中的全球国家CO2排放情况表（分燃料状态）（年）其中的巴西的数据，得到数据后，对数据进行了相应的筛选，其数据展示如下：

表1 1960年-2014年巴西固体燃料消耗产生的CO2排放量原始数据

SgnYear	Cntrnm	Region	IncomeGroup	Solid_CO2m	Liquid_CO2m
1960	巴西	拉丁美洲	中等偏上	4968.79	39049.88
1961	巴西	拉丁美洲	中等偏上	4682.76	41503.11
...	...	...	...	...	...
2014	巴西	拉丁美洲	中等偏上	73666.36	339028

3理论

略

4 实证分析

巴西固体燃料消耗产生的CO2排放量描述性统计分析

首先展示原始数据（前6行），如下图，随后进行整体数据的描述性统计分析：

表3  整体数据描述性统计

		Solid_CO2m			Liquid_CO2m
min		4683			39050
1st Qu		9487			118811
median		35750			150336
mean		32212			161237
3st Qu		48522			229956
max		73666			339029
	SgnYear		Cntrnm	Region		IncomeGroup
Length	55		55	55		55
calss	character		character	character		character
mode	character		character	character		character

从表3可以看出，对巴西固体和液体燃料消耗产生的CO2排放量以及其他数据进行了描述性统计，得到了最大最小值，均值以及1/4分位数和3/4分位数，其中前四个变量为非数值型变量。且下图4画出了1960年-2014年巴西固体燃料消耗产生的CO2排放量的时序图。

ARIMA模型的构建

进行ARIMA模型构建之前，要对时间序列数据纯随机性和平稳性检验。可以判断数据是否具有建模的价值以及是否适合ARIMA模型。下面对巴西固体燃料消耗产生的CO2排放量数据进行纯随机性检验和平稳性检验结果如下表4和表5：

表4  纯随机检验

滞后期数	卡方统计量	P值
滞后6期P值	234.39	0.000
滞后12期P值	350.1	0.000

下面进行自动定阶的函数，计算得到模型应该采用ARIMA(2,1,2)，拟合得到模型系数：

表 7 模型定阶系数

Coefficients:
s.e.	ar1	ar2	ma1	ma2	drift
	-0.1213	-0.8560	-0.1862	0.9513	1236.9922
	0.1035	0.1002	0.0863	0.1673	330.2231
Sigma^2=8135344: likelihood=-505.11
Aic=1022.23 AICc=1024.01 BIC=1034.16

随后进行模型判断和误差的计算：

最后进行预测，预测3期，即未来3年巴西的巴西固体燃料消耗产生的CO2排放量，

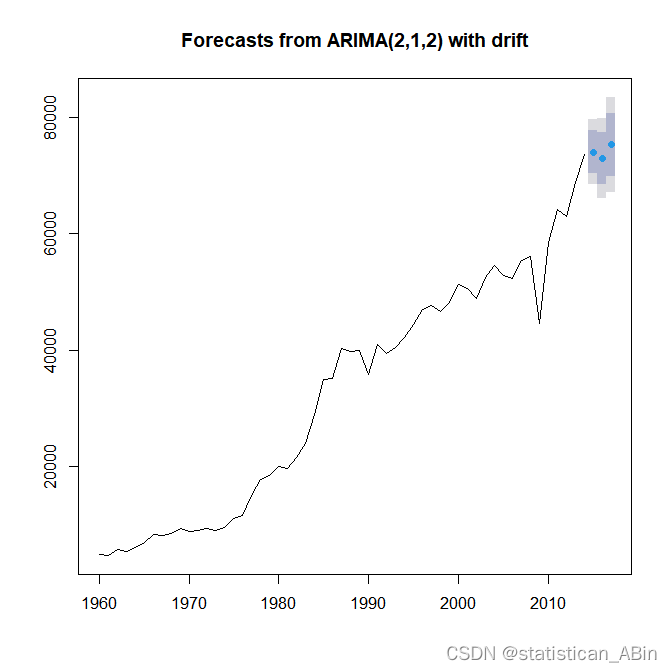
5 结论

巴西1960年-2014年固体燃料消耗产生的CO2排放量来进行分析和预测，针对特定的数据进行建模分析，最终得出相应的结论。ARIMA模型的预测方面的还可行性，针对预测的结果，可以对政策调整和其他方面的策略判断做出相应的参考，在理论上具有一定的参考价值。

本文代码
 

dataset1<- read.xlsx("巴西不同燃料的排放量.xlsx", sheet = 1)
dataset1

###首先展示数据前6行
head(dataset1,6)

###随后对整体数据进行描述性添加分析
summary(dataset1)

###画出1960年-2014年巴西固体燃料消耗产生的CO2排放量的时间序列图形

dataset1$Solid_CO2Emission
HG_I<-ts(dataset1$Solid_CO2Emission,start=c(1960),frequency=1)
HG_I
plot(HG_I,type="o",pch=20,main="1960年-2014年巴西固体燃料消耗产生的CO2排放量时间序列图",xlab = "年份/Y",ylab="排放量",col = "green")

#白噪声检验
for(i in 1:2) print(Box.test(HG_I,type = "Ljung-Box",lag=6*i))
###P值很少，很明显为非白噪声，可继续建模


library(stats)
ndiffs(HG_I)
###结果显示为需要1阶差分
##但是个人看 2 阶才能平稳
diff.HG_I<-diff(HG_I,2) 
plot(diff.HG_I,main='2阶差分图')

ADF2<-adf.test(diff.HG_I)  #1阶差分单位根检验
ADF2


# 确定ARIMA模型中的p,q
# 这里有两种方法，一种是凭对知识点的理解通过ACF函数图和PACF函数图自行判断
# p,q的值另一种是通过软件的算法自动预测。
acf(diff.HG_I,main='差分后acf',lag.max = 12)
pacf(diff.HG_I,main='差分后pacf',lag.max = 12)


###模型拟合
HG_I.fit<-auto.arima(HG_I)
HG_I.fit 


#模型预测
per_HG_I<-forecast(HG_I.fit,h=3)
per_HG_I
plot(per_HG_I)

巴西co2数据和BG