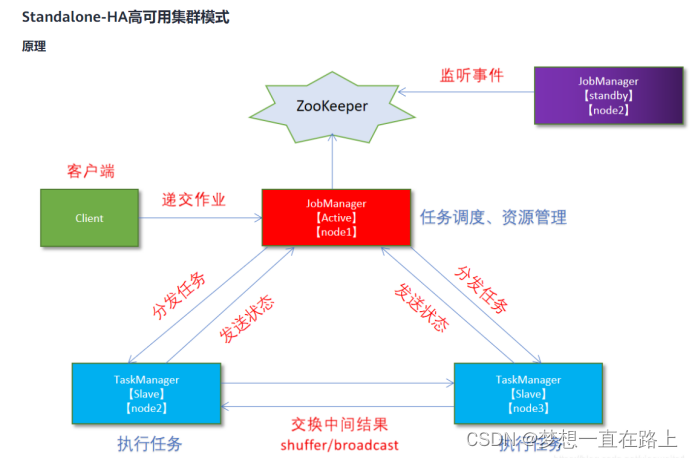
1.在Windows的WSL2上安装Ubuntu
流程可参考:https://www.bilibili.com/video/BV1mX4y177dJ
注意:中间可能需要使用命令wsl --update更新一下wsl。
2.WSL数据迁移
按照下面流程:开始菜单->设置->应用->安装的应用->搜索“ubuntu”->点选3个点->移动->移动到"非C盘的其他盘"
3.为WSL适配图形化界面
参考:https://www.bilibili.com/video/BV1mX4y177dJ
启动图形化界面的命令是sudo startxfce4
4.安装cuda
参考:https://zhuanlan.zhihu.com/p/683058297
nvidia-smi命令的解释参考:https://blog.csdn.net/daydayup858/article/details/131633445
注意:一定要先查看nvidia-smi命令中的显示的支持的cuda的最高版本,然后再去下载对应版本的cuda。
如果装错了cuda版本,可以参考这篇文章卸载已安装的cuda:https://blog.csdn.net/ziqibit/article/details/129935737
如果显示nvcc not found,请参考:https://blog.csdn.net/Maggie_JK/article/details/132666245
5.安装cuDNN
参考:https://zhuanlan.zhihu.com/p/683058297
卸载cuDNN的方式是和卸载cuda类似的。
完成安装后可以使用参考链接的内容进行验证,cuDNN是否正确安装。
7.安装miniconda
参考:https://zhuanlan.zhihu.com/p/683058297
安装完conda之后,创建新的环境,并切换到新环境
8.安装pytorch
参考:https://zhuanlan.zhihu.com/p/683058297
9.安装vscode
去vscode官网安装vscode
vscode上安装wsl扩展包
之后参考https://zhuanlan.zhihu.com/p/683058297
https://learn.microsoft.com/zh-cn/windows/wsl/tutorials/wsl-vscode
9.代码测试
参考:https://www.bilibili.com/video/BV1B14y1W7z3
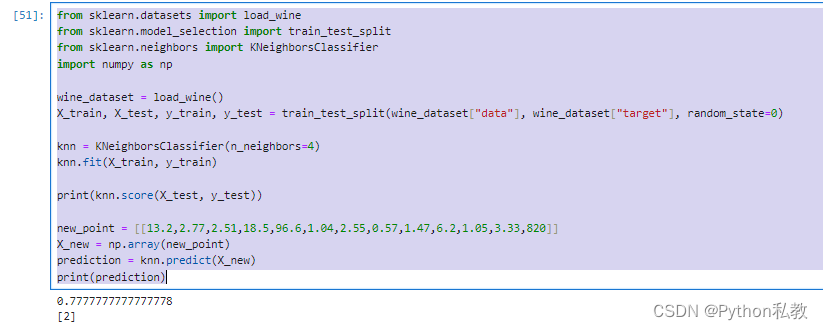
我的测试结果:

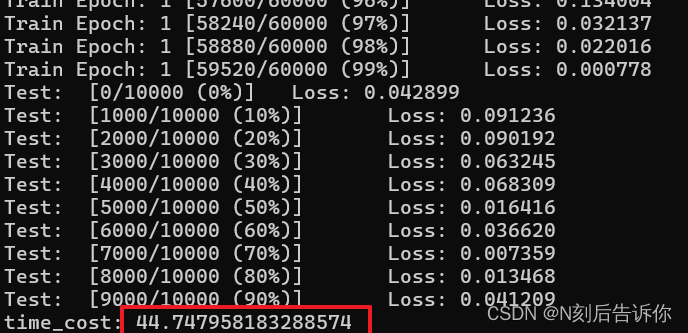
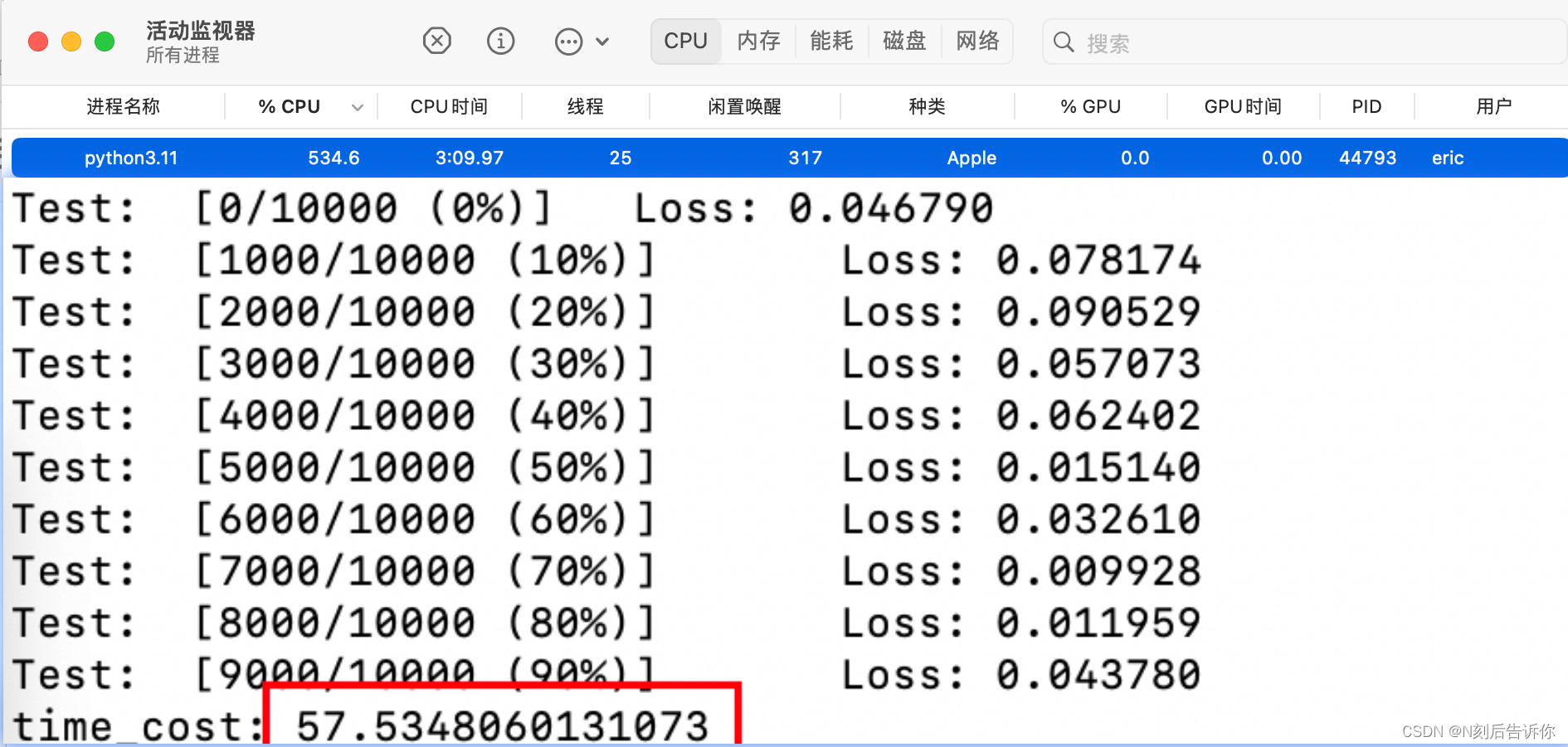
在Mac上只使用CPU
在Mac上使用GPU
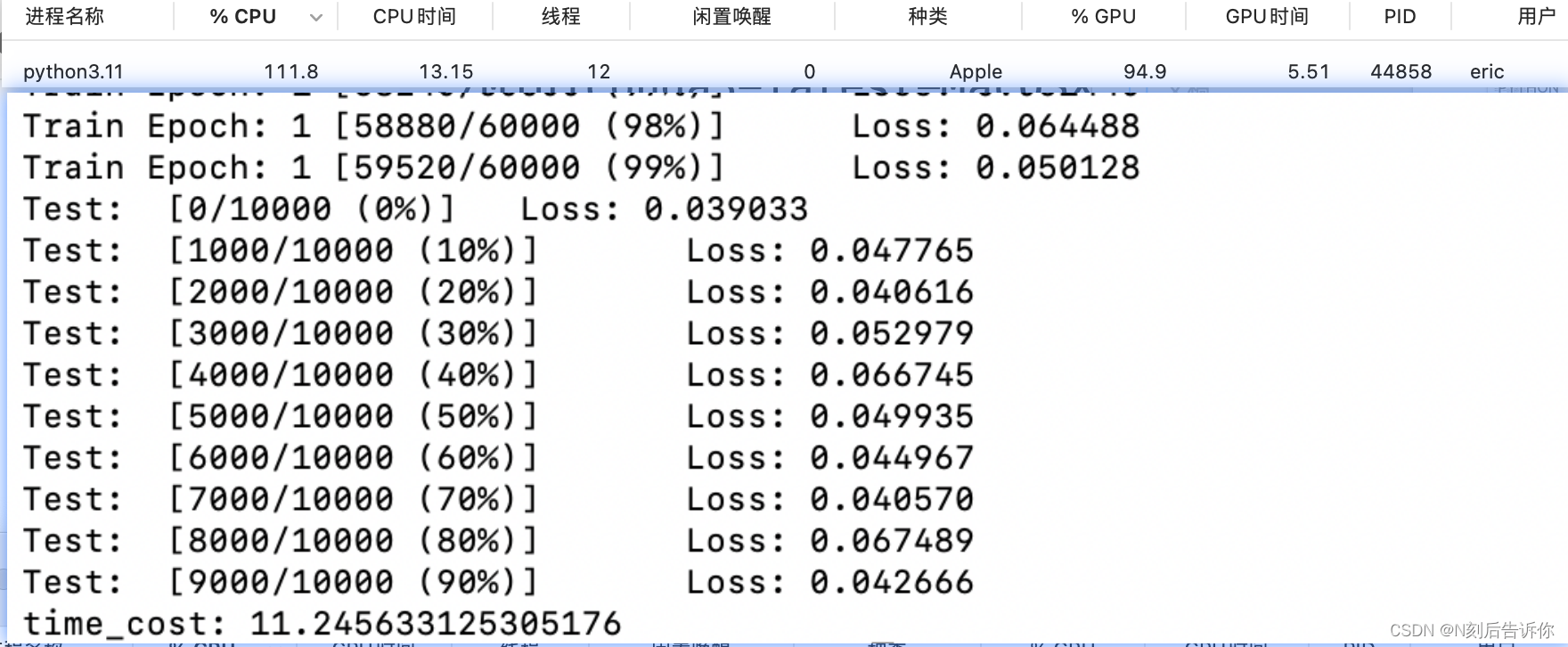
10.其他
如何优雅的使用WSL:https://www.bilibili.com/video/BV1Ku4y1f7nq





![[Cocos Creator 3.5赛车游戏]第三节 新建项目](https://img-blog.csdnimg.cn/img_convert/d04a15aebaac2ed8004a6a118628d987.png)