一、最长定差子序列

1218. 最长定差子序列

算法原理：

💡细节：

1.正常创建dp表，分析状态转移方程：可能b存在于多个不同的位置，那么要用哪个下标的dp呢？

用最后一个b的，因为用前面的可能后面还存在c可以满足条件（a-b=b-c)

2.优化1：那么多b值，那么普通查找只能从后面开始一个一个找，为了提高效率，可以将b+dp[j]的值放入哈希表中

3.优化2：既然都将dp值放入哈希表中，那么可以直接不用new一个dp表，直接在哈希表中做动态规划，这样也同样有下标对应，只是由数组变为哈希表（k,v)

4.初始化为最小值

class Solution {
    public int longestSubsequence(int[] arr, int difference) {
        Map<Integer,Integer> hash = new HashMap<>();//分别放arr[i],dp[i]

        int ret = 1;
        for(int a:arr) {
            hash.put(a,hash.getOrDefault(a-difference,0)+1);
            ret = Math.max(ret,hash.get(a));
        }

        return ret;

    }
}

---

 二、最长的斐波那契数列的长度

873. 最长的斐波那契子序列的长度

算法原理：

💡细节： 

1.如果只用一维数组表示dp，肯定是表示不出来的，当一维dp去找前一个数字nums[j]的时候，由于dp表示的是这个位置结尾的最长长度，并不知道倒数第二个斐波那契数的位置，所以需要多一个参数表示

2.优化：通过b,c去找a的时候，需要遍历数组，为了提高效率，将下标和对应的元素放入哈希表中

3.初始化：虽然可能结果为0，但是直接初始化为2，可以少考虑状态转移方程两种情况，同时这样处理要注意返回值处理

class Solution {
    public int lenLongestFibSubseq(int[] arr) {
        //哈希表优化
        Map<Integer,Integer> hash = new HashMap<>();
        int n = arr.length;
        for(int i=0;i<n;i++) hash.put(arr[i],i);

        int[][] dp = new int[n][n];
        //初始化
        for(int i=0;i<n;i++) 
            for(int j=0;j<n;j++) 
                dp[i][j] = 2;

        int ret =2;
        for(int j=2;j<n;j++) {//最后一个数得从第3个位置开始
            for(int i=1;i<n;i++) {//倒数第二个数得从第2个位置开始
                int a = arr[j]-arr[i];//第一个数的大小
                if(a<arr[i]&&hash.containsKey(a)) {
                    dp[i][j] = dp[hash.get(a)][i] + 1;
                }
                ret = Math.max(ret,dp[i][j]);
            }
        }

        return ret<3?0:ret;
    }
}

---

三、最长等差数列

1027. 最长等差数列

算法原理：

 💡细节： 

1.同上题一样，一维dp数组只能知道长度，不知道等差数列啥样，所以需要多开一个参数，用两个数来确定第一个数的位置

2.状态转移方程的确定：分三种情况，第一个数a是否存在+a存在是否在b（第二个数）的左边

（1）a存在&&a在b的左边 ->dp[i][j] = dp[k][i] +1(其中k为第一个数的下标，需要在数组中找）

（2）a存在but a在b的右边-> dp = 2（由于dp的设置，只要两个不同的值i和j）

（3）a不存在 -> dp = 2

3.遍历优化：找k下标的方式O（n**3）优化

（1)第一种优化方式：在dp之前，将<元素，下标数组>放入哈希表中->可行，但是当数组下标太多，那么还是趋于O（n**3）

（2)第二种优化方式：一边dp，一边保存<元素，i下标>放入哈希表，注意第一个数遍历不到，需要在遍历之前先加入哈希表

4.填表方式：两种方式，先确定倒数第一个数，或者先确定倒数第二个数

but这里只能先确定倒数第二个数i，因为需要考虑dp之前hash表中的元素，因为k需要<i，所以不能将元素太早加入hash表中，要找i之前的k（所以这里的k需要是i下标之前的哈希表）

class Solution {
    public int longestArithSeqLength(int[] nums) {
        int n = nums.length;

        Map<Integer,Integer> hash = new HashMap<>();//<元素，下标>
        hash.put(nums[0],0);

        int[][] dp = new int[n][n];

        //初始化
        for(int i=0;i<n;i++) 
            Arrays.fill(dp[i],2);
        
        int ret = 2;
        for(int i=1;i<n;i++) {//固定倒数第一个数
            for(int j=i+1;j<n;j++) {//固定倒数第二个数
                int a = 2*nums[i]-nums[j];//第一个数
                if(hash.containsKey(a)) {
                    dp[i][j]=dp[hash.get(a)][i]+1;
                    ret = Math.max(ret,dp[i][j]);
                }
            }
            hash.put(nums[i],i);//每次i换位置就将(nums[i],i)放入哈希表
        }
        return ret;
    }
}

---

四、等差数列的划分

446. 等差数列划分 II - 子序列

算法原理：

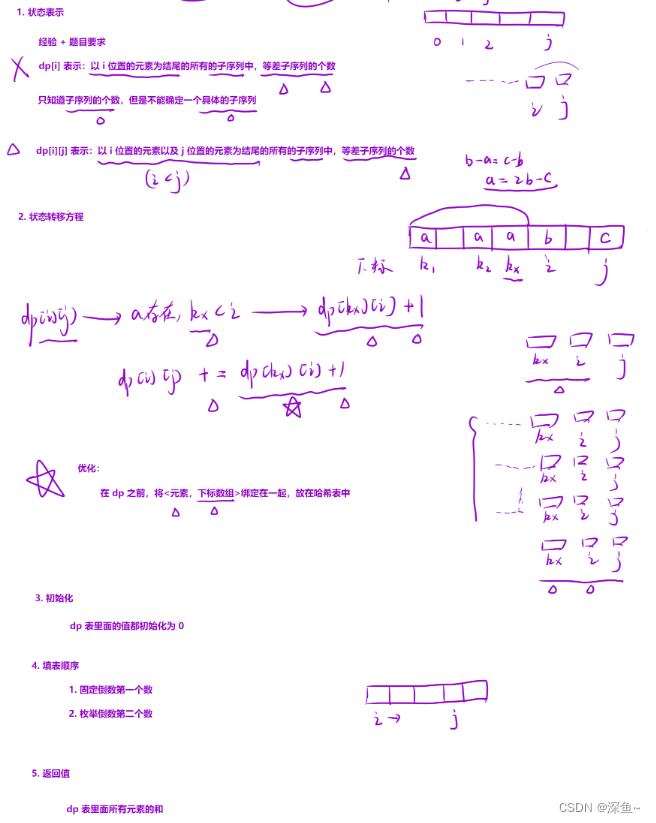
  💡细节： 

1.同上一题，一维dp数组无法判断是否能构成等差数列，只能知道子序列的个数，但是不能确定一个具体的子序列

2.状态转移方程：由于这里a可能有多个位置，but这里不只是看最后一个位置，而是每个位置都需要考虑，因为dp表示的是等差数列的个数，而不是最大长度

dp[i][j] +=dp[k][i]+1 (有多少个加多少个）

3.找k下标遍历优化：可以在dp之前，将<元素，下标数组>存入哈希表中

4.返回值：dp表的和（因为是个数）

5.代码注意：因为题目数据保证答案是一个 32-bit 整数，怕运算的时候越界，需要将int a改为long，同时Map第一个参数改为Long ，tmp也改为long

class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        int n = nums.length;

        int[][] dp = new int[n][n];

        Map<Long,List<Integer>> hash = new HashMap<>();
        //把<元素，下标数组>存入hash
        for(int i=0;i<n;i++) {
            long tmp = nums[i];
            if(!hash.containsKey(tmp)) {//看以前是否创建了对应的下标数组
                hash.put(tmp,new ArrayList<>());
            }
            hash.get(tmp).add(i);//将下标放入下标数组
        }

        int sum=0;
        for(int j=2;j<n;j++) {
            for(int i=1;i<j;i++) {
                long a = 2L*nums[i]-nums[j];
                if(hash.containsKey(a)) {//看第一个数a是否存在
                    for(int k:hash.get(a)) {
                        if(k<i) dp[i][j]+=dp[k][i]+1;
                        else break;//可能比i大的k有多个
                    }
                }
                sum+=dp[i][j];
            }
        }
        return sum;
    }
}