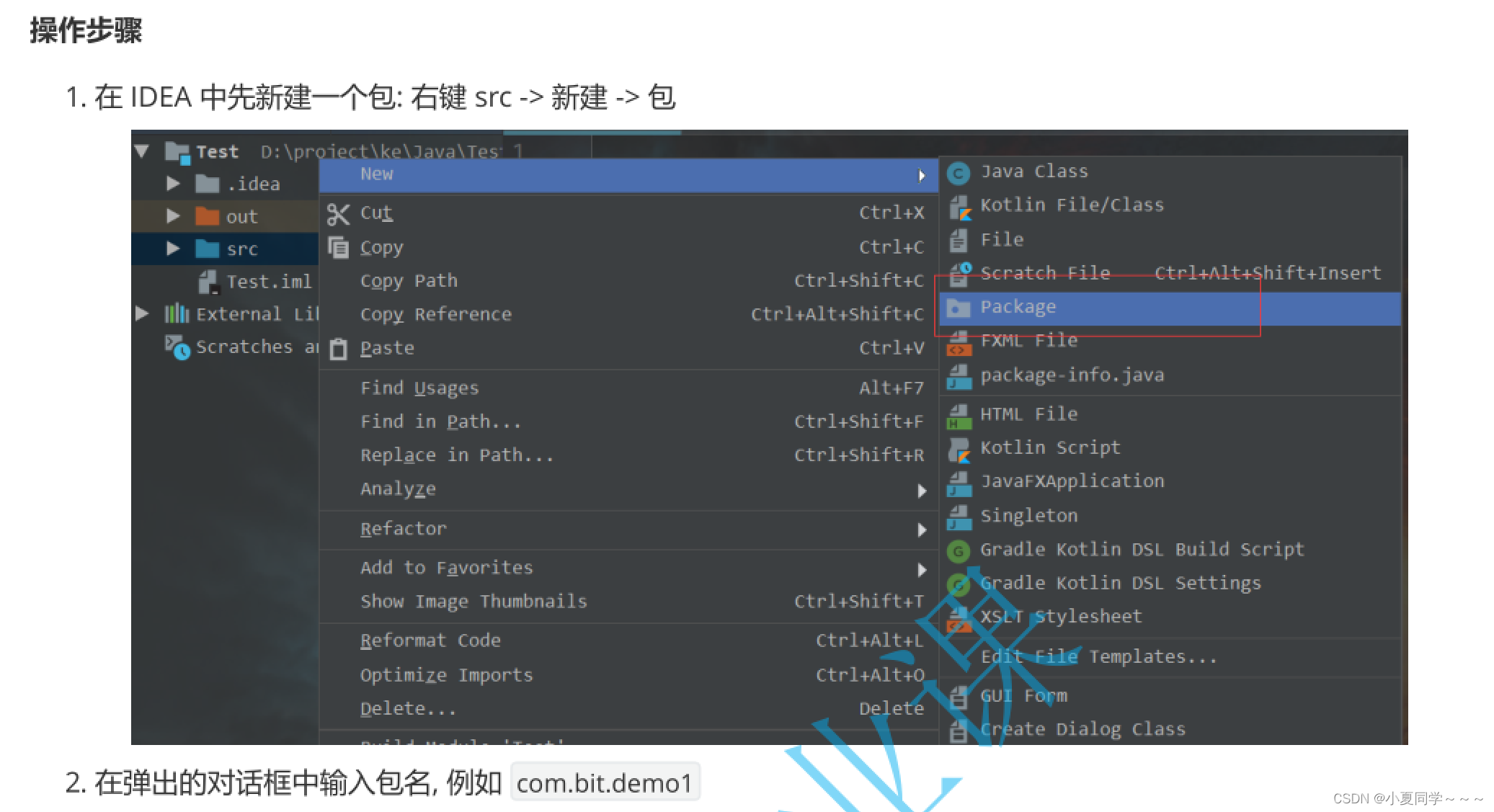
一、不相交集合的操作
不相交集合的数据结构维护了一组不相交动态集的集合 ,用集合中的某个成员作为代表标识集合。
集合在没有修改的情况下每次访问代表得到的答案是相同的,此外在其它一些应用中,可能按照规定选择集合的代表,例如选择每个集合中关键字最小的元素作为代表。
设 x 为一个对象,对不相交集合数据结构的操作:
1.MAKE-SET(x):建立一个新集合,唯一元素就是 x ,由于各个集合是不相交的,x 不会出现在其他的集合中
2.FIND-SET(x):返回一个指针,指向包含 x (唯一)的集合代表 如果已经有指针指向 x ,无需再在数据结构中搜索 x
3.UNION(x,y):将包含 x 和 y 的两个动态集合(表示为 Sx 和 Sy)合并成一个新的集合,即两个集合的并集。 并集中的任何一个元素都可以作为代表(通常实现为 Sx 或 Sy 元素的代表)。由于要求各个元素不相交,合并后需要删除 Sx 和 Sy 集合,通常将一个集合并入另一个集合作为删除操作。 当共有n个元素时,最多执行 n-1 次UNION操作。
不相交集合的应用——确定无向图的连通分量
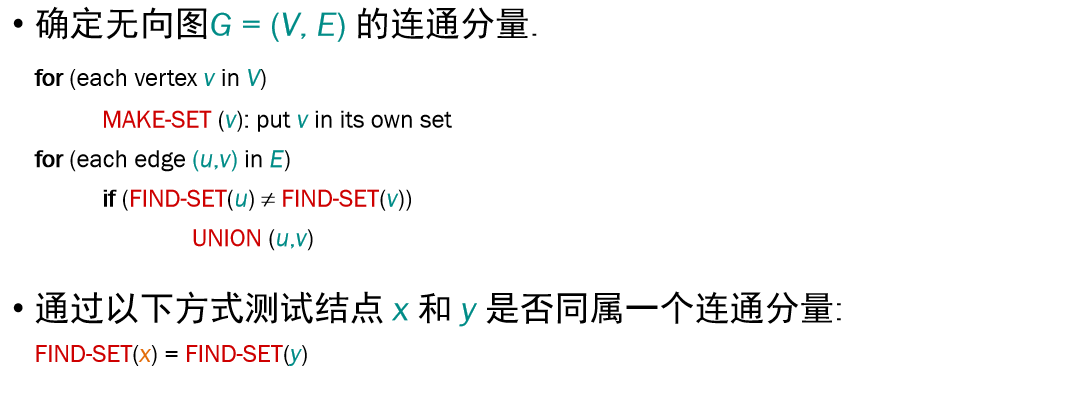
在开始时,需要通过 MAKE-SET(v) 操作将每个节点 v 都放入子集的集合中,再对处理的边(u,v)将包含 u 和 v 的集合合并(前提是两个集合本身不相交,即集合代表不相同)。
判断两个节点是否在同一个集合中,即所属集合的集合代表不相同
FIND-SET(x) ! = FIND-SET(y)
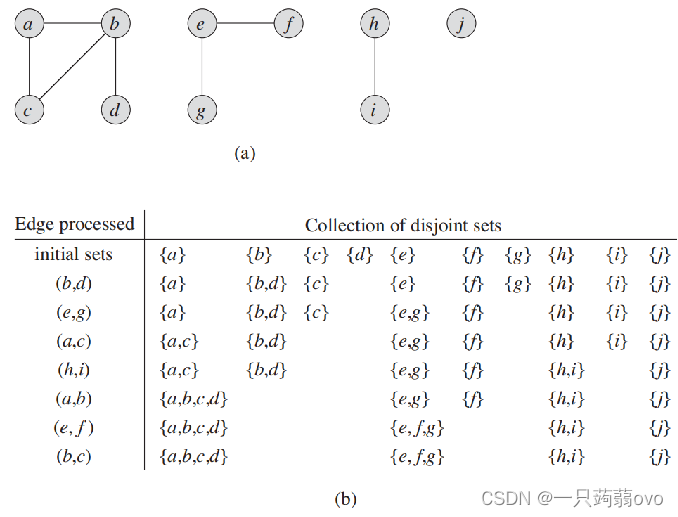
Edge processed:对两点之间边处理顺序
二、不相交集合的链表表示
1.相关概念
每个集合用一个链表来表示,链表的第一个节点就是代表,每个集合对象 set 包含 head 指针 和 tail 指针,分别指向链表中的第一个节点和最后一个节点。
链表中的每个节点都包含一个集合成员(元素),指向链表中下一个节点的指针,指回到集合对象的指针
2.不相交集合的链表操作
① MAKE-SET(x) :
创建一个只有 x 节点的新的链表 时间开销 O(1)
② FIND-SET (x):
沿着 x 对象的返回指针返回到集合对象,然后返回 head 指针指向的节点。 时间开销 O(1)
③ UNION(x,y):
1.将包含 y 的链表添加到包含 x 的链表
2.将包含 x 的链表的代表 作为 y 中节点的代表
3.更新包含 y 链表中各个元素的代表指针 包含 n 个操作的序列可能会花费时间
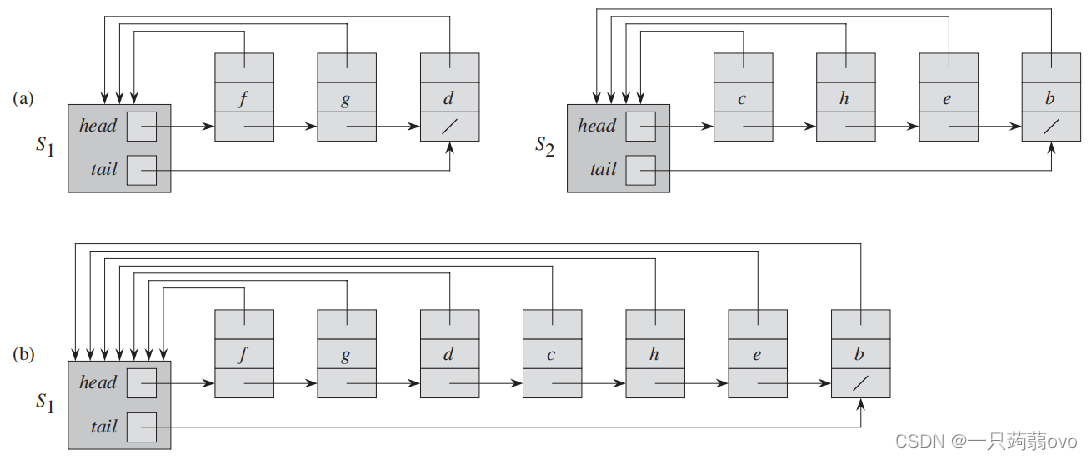
合并的简单实现:
将长链表插入到短链表之中 总开销是 平均开销是Θ(n)
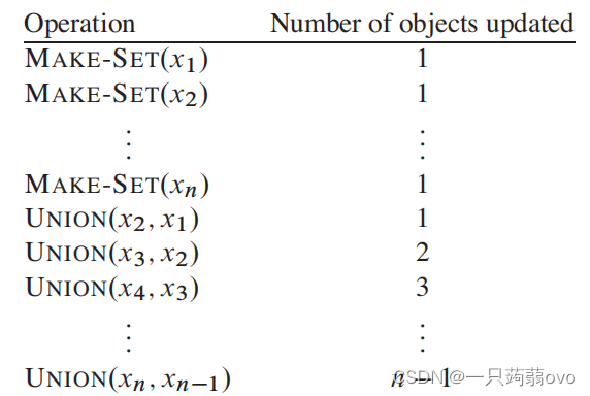
3.一种加权合并的启发式策略
将链表的长度作为权值并维护链表长度,合并时将短的链表拼接到长的链表末尾,
定理:使用不相交集合的链表表示和加权合并的启发式策略,一个具有 m 个 MAKE-SET FIND-SET 和 UNION 操作的序列 (其中 n 个 为 MAKE-SET操作),需要的时间为
三、不相交集合森林
在不相交集合实现中,使用有根树来表示集合,树中的每个节点包含一个成员,每棵树代表一个集合。 在不相交集合森林中,每个成员仅指向他的父节点(根节点指向其自己),并且每棵树的根是集合的代表。
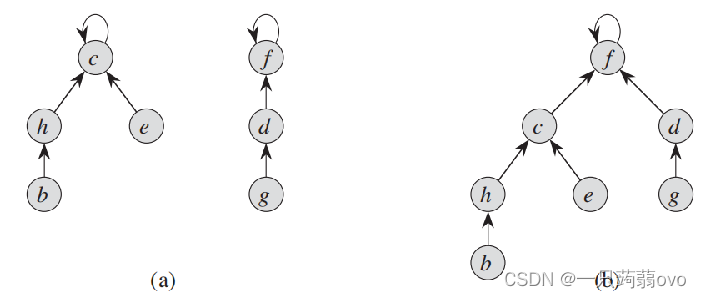
1.不相交集合森林的操作
①MAKE-SET : 建立一个包含节点 x 的新树,并且其的父节点指向自己(根节点)
void MAKE-SET(int x)
{
x.p=x;
x.rank=0;
return ;
}②FIND-SET(x) :返回 x 所在树的集合代表(根节点)。
FIND-SET(x) 用于鉴定集合是否包含元素 x
FIND-SET (x) 和 FIND-SET (y) 返回相同的值,当且仅当元素 x 和 y 同属一个集合
int FIND-SET (int x)
{
if (x≠x.p) // x不是根
x.p=FIND-SET(x.p);
return x.p;
}③ UNION(x,y) :合并包含 x 和 y 的集合的树
若两棵树的根的秩不相同,则将具有较小秩的根点的父指针指向具有较大秩的根结点;
若两棵树的根的秩相同,则任意选择两个根中的一个作为父结点,并将它的秩加一。
一颗二项树的节点的秩(rank)等于它的儿子节点的个数,
void UNION (int x,int y)
{
LINK(FIND-SET(x), FIND-SET(y));
}
void LINK(int x,int y)
{
if(x.rank>y.rank)
y.p=x;
else x.p=y;
if(x.rank==y.rank)
y.rank=y.rank+1;
return ;
}
④ 节点数据结构
使用包含两个字段的结点: element and parent
使用数组 table[] ,其中 table[x] 是一个指向元素 x 的指针 为了执行 FIND-SET (x) 操作, 从 table[i] 标明的结点开始,顺着parent 字段,直到找到结点,使得 parent 字段值为 null 返回根节点的 element
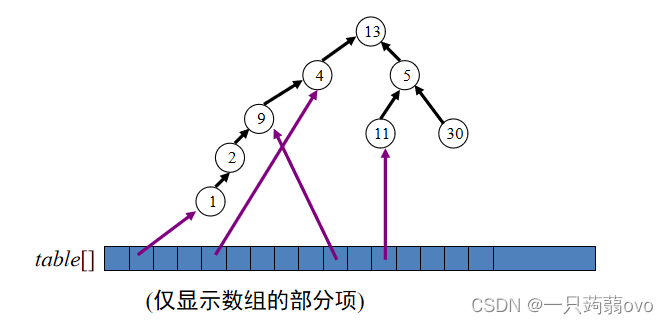
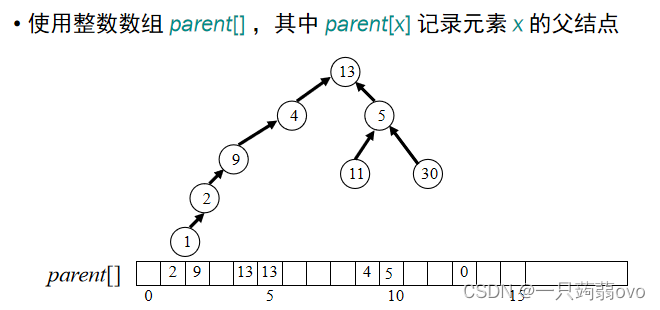
2.两条启发式规则(改进运行时间)
① 按秩合并:执行 UNION 操作时,通过权重或者树高操作
树的根节点必须要么记录树高,要么记录元素个数.
当使用树高规则时,仅当两棵树高度相等时,树高会增加.
当使用权重规则时,新树的权重是两个子树的权重之和.
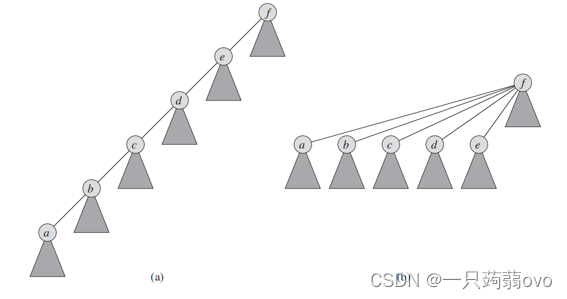
树高规则:将树高小的树作为作为树高大的树的子树
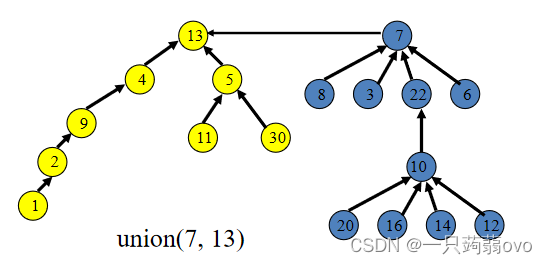
权重规则:包含元素少的那棵树作为元素多的子树
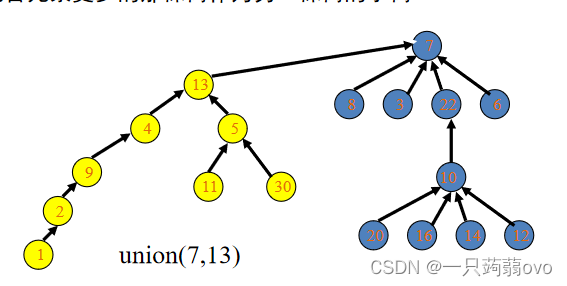
②路径压缩 :缩短查找根节点过程中的路径
在FIND-SET操作中,可以使查找路径中的每个结点直接指向根

![[ROS 系列学习教程] 建模与仿真 - URDF 建模实践](https://img-blog.csdnimg.cn/direct/bc0104b3ddfd45309df5c295080cb9c0.png#pic_center)



![BUUCTF靶场[MISC]wireshark、被嗅探的流量、神秘龙卷风、另一个世界](https://img-blog.csdnimg.cn/direct/25715a70b4ee4f5d86a2660a4d1c27ee.png)