代码随想录算法训练营第二十五天:树的最后学习
如果不对递归有深刻的理解,本题有点难 单纯移除一个节点那还不够,要修剪!
#669. 修剪二叉搜索树
力扣题目链接(opens new window)
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。


#算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** :你修剪的方式不对,我来给你纠正一下!| LeetCode:669. 修剪二叉搜索树 ****(opens new window)**** ,相信结合视频在看本篇题解,更有助于大家对本题的理解。
#思路
相信看到这道题目大家都感觉是一道简单题(事实上leetcode上也标明是简单)。
但还真的不简单!
#递归法
直接想法就是:递归处理,然后遇到 root->val < low || root->val > high 的时候直接return NULL,一波修改,赶紧利落。
不难写出如下代码:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr || root->val < low || root->val > high) return nullptr;
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
然而[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的,还要考虑节点0的右子树。
我们在重新关注一下第二个示例,如图:
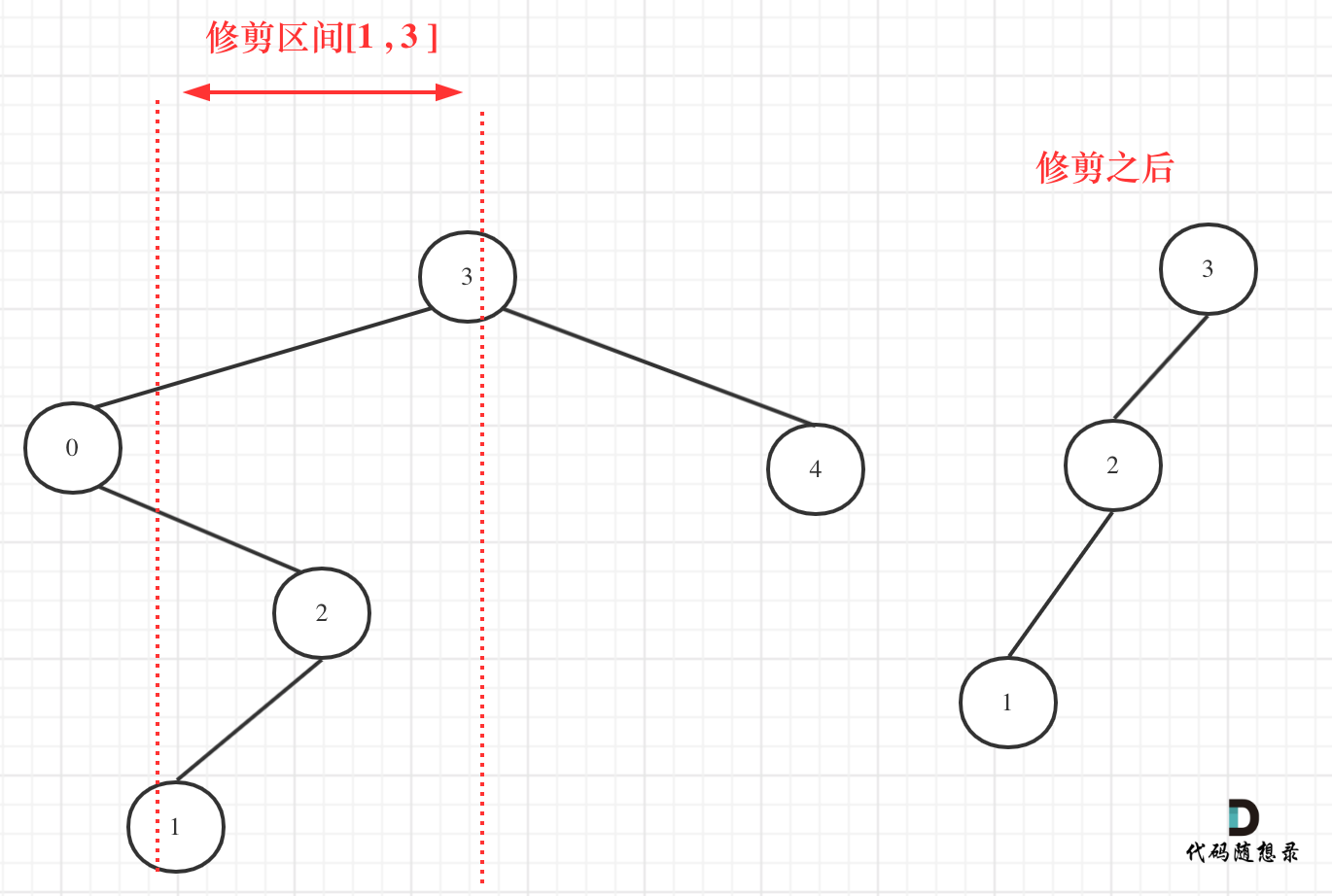
所以以上的代码是不可行的!
从图中可以看出需要重构二叉树,想想是不是本题就有点复杂了。
其实不用重构那么复杂。
在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点0从二叉树中移除),如图:
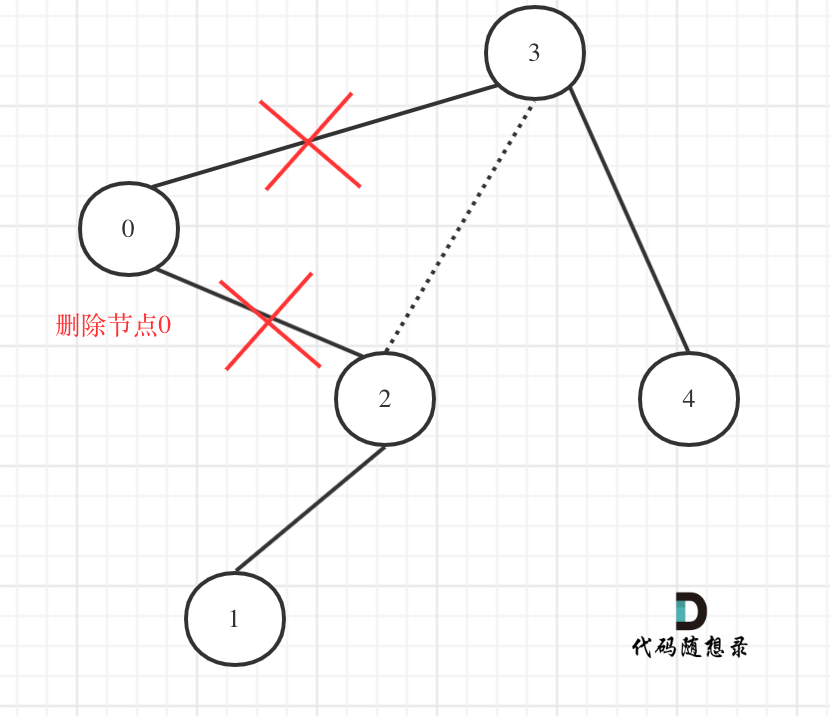
理解了最关键部分了我们再递归三部曲:
- 确定递归函数的参数以及返回值
这里我们为什么需要返回值呢?
因为是要遍历整棵树,做修改,其实不需要返回值也可以,我们也可以完成修剪(其实就是从二叉树中移除节点)的操作。
但是有返回值,更方便,可以通过递归函数的返回值来移除节点。
这样的做法在二叉树:搜索树中的插入操作 **(opens new window)** 和二叉树:搜索树中的删除操作 **(opens new window)** 中大家已经了解过了。
代码如下:
TreeNode* trimBST(TreeNode* root, int low, int high)
- 确定终止条件
修剪的操作并不是在终止条件上进行的,所以就是遇到空节点返回就可以了。
if (root == nullptr ) return nullptr;
- 确定单层递归的逻辑
如果root(当前节点)的元素小于low的数值,那么应该递归右子树,并返回右子树符合条件的头结点。
代码如下:
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
return right;
}
如果root(当前节点)的元素大于high的,那么应该递归左子树,并返回左子树符合条件的头结点。
代码如下:
if (root->val > high) {
TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
return left;
}
接下来要将下一层处理完左子树的结果赋给root->left,处理完右子树的结果赋给root->right。
最后返回root节点,代码如下:
root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
return root;
此时大家是不是还没发现这多余的节点究竟是如何从二叉树中移除的呢?
在回顾一下上面的代码,针对下图中二叉树的情况:
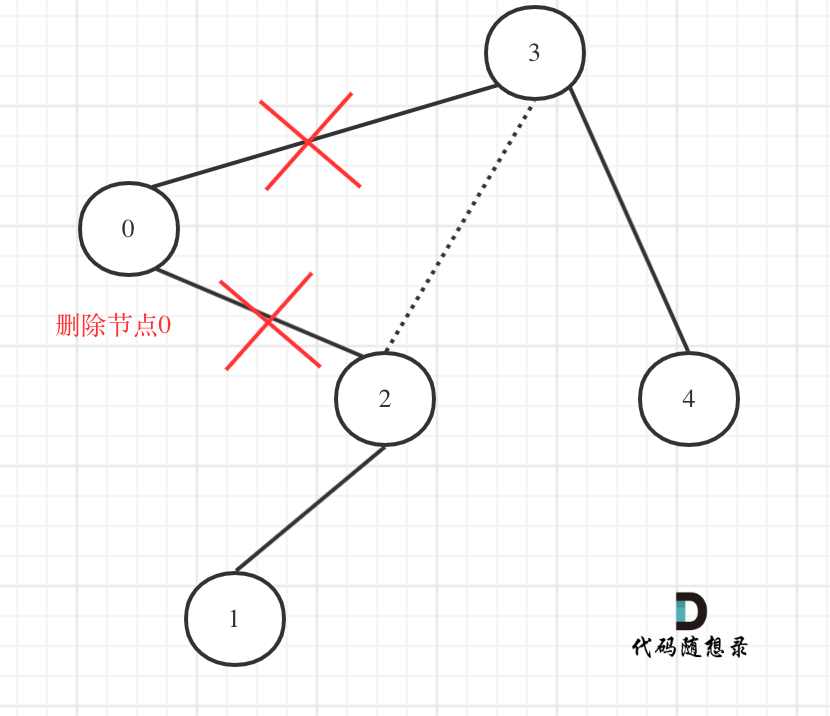
如下代码相当于把节点0的右孩子(节点2)返回给上一层,
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
return right;
}
然后如下代码相当于用节点3的左孩子 把下一层返回的 节点0的右孩子(节点2) 接住。
root->left = trimBST(root->left, low, high);
此时节点3的左孩子就变成了节点2,将节点0从二叉树中移除了。
最后整体代码如下:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr ) return nullptr;
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
return right;
}
if (root->val > high) {
TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
return left;
}
root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
return root;
}
};
精简之后代码如下:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr) return nullptr;
if (root->val < low) return trimBST(root->right, low, high);
if (root->val > high) return trimBST(root->left, low, high);
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
只看代码,其实不太好理解节点是如何移除的,这一块大家可以自己再模拟模拟!
#迭代法
因为二叉搜索树的有序性,不需要使用栈模拟递归的过程。
在剪枝的时候,可以分为三步:
- 将root移动到[L, R] 范围内,注意是左闭右闭区间
- 剪枝左子树
- 剪枝右子树
代码如下:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int L, int R) {
if (!root) return nullptr;
// 处理头结点,让root移动到[L, R] 范围内,注意是左闭右闭
while (root != nullptr && (root->val < L || root->val > R)) {
if (root->val < L) root = root->right; // 小于L往右走
else root = root->left; // 大于R往左走
}
TreeNode *cur = root;
// 此时root已经在[L, R] 范围内,处理左孩子元素小于L的情况
while (cur != nullptr) {
while (cur->left && cur->left->val < L) {
cur->left = cur->left->right;
}
cur = cur->left;
}
cur = root;
// 此时root已经在[L, R] 范围内,处理右孩子大于R的情况
while (cur != nullptr) {
while (cur->right && cur->right->val > R) {
cur->right = cur->right->left;
}
cur = cur->right;
}
return root;
}
};
#总结
修剪二叉搜索树其实并不难,但在递归法中大家可看出我费了很大的功夫来讲解如何删除节点的,这个思路其实是比较绕的。
最终的代码倒是很简洁。
如果不对递归有深刻的理解,这道题目还是有难度的!
本题我依然给出递归法和迭代法,初学者掌握递归就可以了,如果想进一步学习,就把迭代法也写一写。
构造二叉搜索树,一不小心就平衡了
#108.将有序数组转换为二叉搜索树
力扣题目链接(opens new window)
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:

#算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** :构造平衡二叉搜索树!| LeetCode:108.将有序数组转换为二叉搜索树 ****(opens new window)**** ,相信结合视频在看本篇题解,更有助于大家对本题的理解。
#思路
做这道题目之前大家可以了解一下这几道:
- 106.从中序与后序遍历序列构造二叉树(opens new window)
- 654.最大二叉树 **(opens new window)** 中其实已经讲过了,如果根据数组构造一棵二叉树。
- 701.二叉搜索树中的插入操作(opens new window)
- 450.删除二叉搜索树中的节点(opens new window)
进入正题:
题目中说要转换为一棵高度平衡二叉搜索树。为什么强调要平衡呢?
因为只要给我们一个有序数组,如果不强调平衡,都可以以线性结构来构造二叉搜索树。
例如 有序数组[-10,-3,0,5,9] 就可以构造成这样的二叉搜索树,如图。
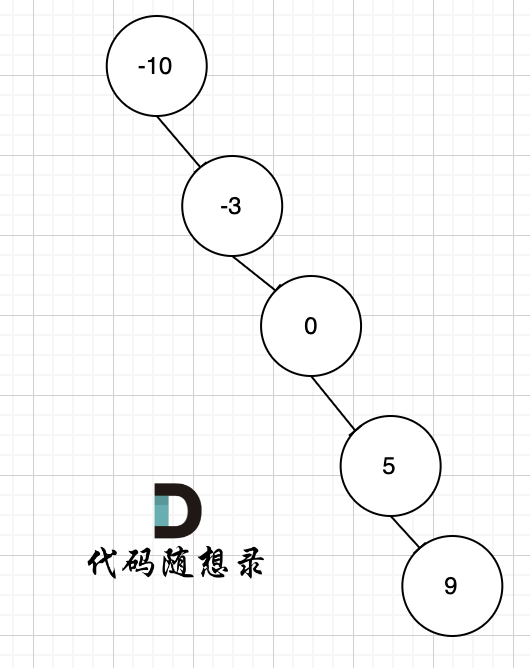
上图中,是符合二叉搜索树的特性吧,如果要这么做的话,是不是本题意义就不大了,所以才强调是平衡二叉搜索树。
其实数组构造二叉树,构成平衡树是自然而然的事情,因为大家默认都是从数组中间位置取值作为节点元素,一般不会随机取。所以想构成不平衡的二叉树是自找麻烦。
在二叉树:构造二叉树登场! **(opens new window)** 和二叉树:构造一棵最大的二叉树 **(opens new window)** 中其实已经讲过了,如果根据数组构造一棵二叉树。
本质就是寻找分割点,分割点作为当前节点,然后递归左区间和右区间。
本题其实要比二叉树:构造二叉树登场! **(opens new window)** 和 二叉树:构造一棵最大的二叉树 **(opens new window)** 简单一些,因为有序数组构造二叉搜索树,寻找分割点就比较容易了。
分割点就是数组中间位置的节点。
那么为问题来了,如果数组长度为偶数,中间节点有两个,取哪一个?
取哪一个都可以,只不过构成了不同的平衡二叉搜索树。
例如:输入:[-10,-3,0,5,9]
如下两棵树,都是这个数组的平衡二叉搜索树:
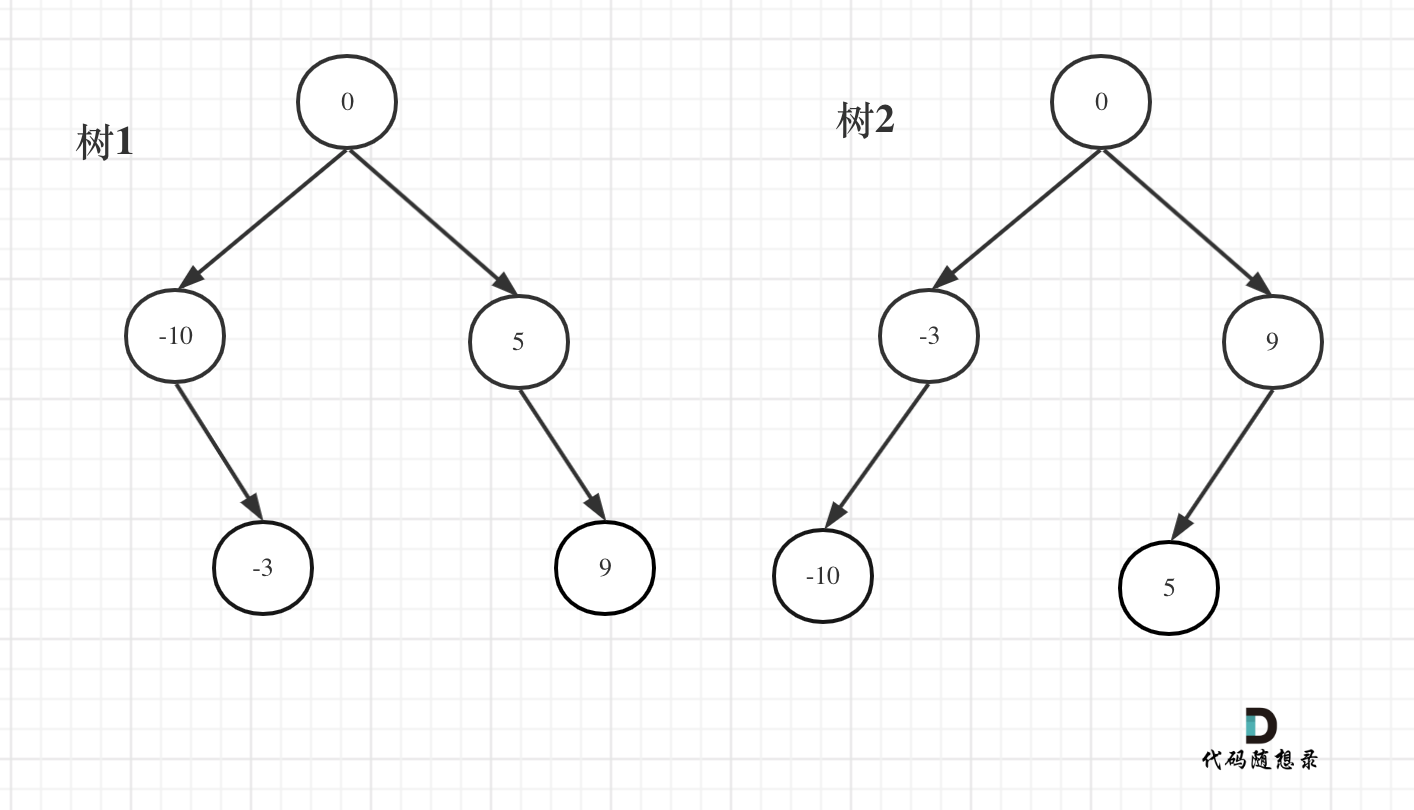
如果要分割的数组长度为偶数的时候,中间元素为两个,是取左边元素 就是树1,取右边元素就是树2。
这也是题目中强调答案不是唯一的原因。 理解这一点,这道题目算是理解到位了。
#递归
递归三部曲:
- 确定递归函数返回值及其参数
删除二叉树节点,增加二叉树节点,都是用递归函数的返回值来完成,这样是比较方便的。
相信大家如果仔细看了二叉树:搜索树中的插入操作 **(opens new window)** 和二叉树:搜索树中的删除操作 **(opens new window)** ,一定会对递归函数返回值的作用深有感触。
那么本题要构造二叉树,依然用递归函数的返回值来构造中节点的左右孩子。
再来看参数,首先是传入数组,然后就是左下标left和右下标right,我们在二叉树:构造二叉树登场! **(opens new window)** 中提过,在构造二叉树的时候尽量不要重新定义左右区间数组,而是用下标来操作原数组。
所以代码如下:
// 左闭右闭区间[left, right]
TreeNode* traversal(vector<int>& nums, int left, int right)
这里注意,我这里定义的是左闭右闭区间,在不断分割的过程中,也会坚持左闭右闭的区间,这又涉及到我们讲过的循环不变量。
在二叉树:构造二叉树登场! **(opens new window)** ,35.搜索插入位置 **(opens new window)** 和59.螺旋矩阵II **(opens new window)** 都详细讲过循环不变量。
- 确定递归终止条件
这里定义的是左闭右闭的区间,所以当区间 left > right的时候,就是空节点了。
代码如下:
if (left > right) return nullptr;
- 确定单层递归的逻辑
首先取数组中间元素的位置,不难写出int mid = (left + right) / 2;,这么写其实有一个问题,就是数值越界,例如left和right都是最大int,这么操作就越界了,在**二分法** ****(opens new window)****中尤其需要注意!
所以可以这么写:int mid = left + ((right - left) / 2);
但本题leetcode的测试数据并不会越界,所以怎么写都可以。但需要有这个意识!
取了中间位置,就开始以中间位置的元素构造节点,代码:TreeNode* root = new TreeNode(nums[mid]);。
接着划分区间,root的左孩子接住下一层左区间的构造节点,右孩子接住下一层右区间构造的节点。
最后返回root节点,单层递归整体代码如下:
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
这里int mid = left + ((right - left) / 2);的写法相当于是如果数组长度为偶数,中间位置有两个元素,取靠左边的。
- 递归整体代码如下:
class Solution {
private:
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left > right) return nullptr;
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
TreeNode* root = traversal(nums, 0, nums.size() - 1);
return root;
}
};
注意:在调用traversal的时候传入的left和right为什么是0和nums.size() - 1,因为定义的区间为左闭右闭。
#迭代法
迭代法可以通过三个队列来模拟,一个队列放遍历的节点,一个队列放左区间下标,一个队列放右区间下标。
模拟的就是不断分割的过程,C++代码如下:(我已经详细注释)
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
if (nums.size() == 0) return nullptr;
TreeNode* root = new TreeNode(0); // 初始根节点
queue<TreeNode*> nodeQue; // 放遍历的节点
queue<int> leftQue; // 保存左区间下标
queue<int> rightQue; // 保存右区间下标
nodeQue.push(root); // 根节点入队列
leftQue.push(0); // 0为左区间下标初始位置
rightQue.push(nums.size() - 1); // nums.size() - 1为右区间下标初始位置
while (!nodeQue.empty()) {
TreeNode* curNode = nodeQue.front();
nodeQue.pop();
int left = leftQue.front(); leftQue.pop();
int right = rightQue.front(); rightQue.pop();
int mid = left + ((right - left) / 2);
curNode->val = nums[mid]; // 将mid对应的元素给中间节点
if (left <= mid - 1) { // 处理左区间
curNode->left = new TreeNode(0);
nodeQue.push(curNode->left);
leftQue.push(left);
rightQue.push(mid - 1);
}
if (right >= mid + 1) { // 处理右区间
curNode->right = new TreeNode(0);
nodeQue.push(curNode->right);
leftQue.push(mid + 1);
rightQue.push(right);
}
}
return root;
}
};
#总结
在**二叉树:构造二叉树登场!** ****(opens new window)****和 二叉树:构造一棵最大的二叉树 ****(opens new window)****之后,我们顺理成章的应该构造一下二叉搜索树了,一不小心还是一棵平衡二叉搜索树。
其实思路也是一样的,不断中间分割,然后递归处理左区间,右区间,也可以说是分治。
此时相信大家应该对通过递归函数的返回值来增删二叉树很熟悉了,这也是常规操作。
在定义区间的过程中我们又一次强调了循环不变量的重要性。
最后依然给出迭代的方法,其实就是模拟取中间元素,然后不断分割去构造二叉树的过程。
538.把二叉搜索树转换为累加树
力扣题目链接(opens new window)
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。
示例 1:
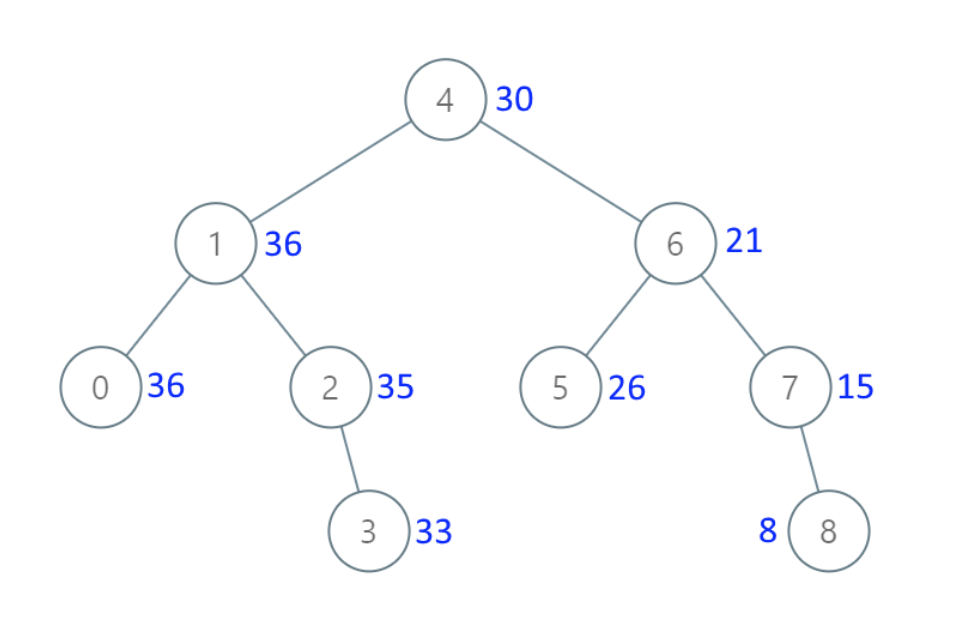
- 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
- 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
- 输入:root = [0,null,1]
- 输出:[1,null,1]
示例 3:
- 输入:root = [1,0,2]
- 输出:[3,3,2]
示例 4:
- 输入:root = [3,2,4,1]
- 输出:[7,9,4,10]
提示:
- 树中的节点数介于 0 和 104 之间。
- 每个节点的值介于 -104 和 104 之间。
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
#算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** :普大喜奔!二叉树章节已全部更完啦!| LeetCode:538.把二叉搜索树转换为累加树 ****(opens new window)**** ,相信结合视频在看本篇题解,更有助于大家对本题的理解。
#思路
一看到累加树,相信很多小伙伴都会疑惑:如何累加?遇到一个节点,然后再遍历其他节点累加?怎么一想这么麻烦呢。
然后再发现这是一棵二叉搜索树,二叉搜索树啊,这是有序的啊。
那么有序的元素如何求累加呢?
其实这就是一棵树,大家可能看起来有点别扭,换一个角度来看,这就是一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13],是不是感觉这就简单了。
为什么变成数组就是感觉简单了呢?
因为数组大家都知道怎么遍历啊,从后向前,挨个累加就完事了,这换成了二叉搜索树,看起来就别扭了一些是不是。
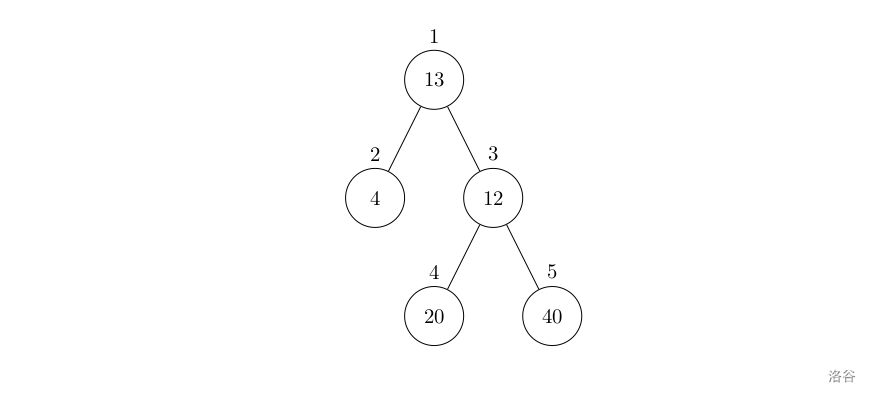
那么知道如何遍历这个二叉树,也就迎刃而解了,从树中可以看出累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,然后顺序累加就可以了。
#递归
遍历顺序如图所示:
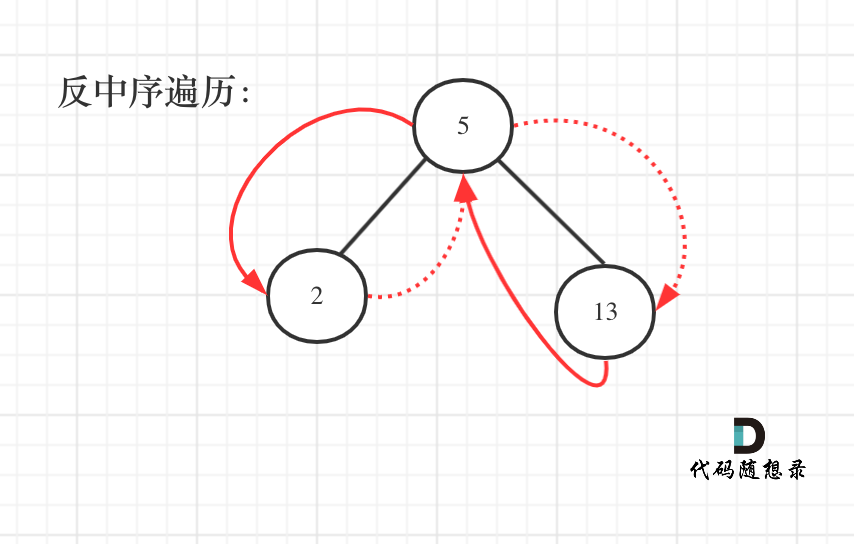
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
pre指针的使用技巧,我们在二叉树:搜索树的最小绝对差 **(opens new window)** 和二叉树:我的众数是多少? **(opens new window)** 都提到了,这是常用的操作手段。
- 递归函数参数以及返回值
这里很明确了,不需要递归函数的返回值做什么操作了,要遍历整棵树。
同时需要定义一个全局变量pre,用来保存cur节点的前一个节点的数值,定义为int型就可以了。
代码如下:
int pre = 0; // 记录前一个节点的数值
void traversal(TreeNode* cur)
- 确定终止条件
遇空就终止。
if (cur == NULL) return;
- 确定单层递归的逻辑
注意要右中左来遍历二叉树, 中节点的处理逻辑就是让cur的数值加上前一个节点的数值。
代码如下:
traversal(cur->right); // 右
cur->val += pre; // 中
pre = cur->val;
traversal(cur->left); // 左
递归法整体代码如下:
class Solution {
private:
int pre = 0; // 记录前一个节点的数值
void traversal(TreeNode* cur) { // 右中左遍历
if (cur == NULL) return;
traversal(cur->right);
cur->val += pre;
pre = cur->val;
traversal(cur->left);
}
public:
TreeNode* convertBST(TreeNode* root) {
pre = 0;
traversal(root);
return root;
}
};
#迭代法
迭代法其实就是中序模板题了,在二叉树:前中后序迭代法 **(opens new window)** 和二叉树:前中后序统一方式迭代法 **(opens new window)** 可以选一种自己习惯的写法。
这里我给出其中的一种,代码如下:
class Solution {
private:
int pre; // 记录前一个节点的数值
void traversal(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur != NULL || !st.empty()) {
if (cur != NULL) {
st.push(cur);
cur = cur->right; // 右
} else {
cur = st.top(); // 中
st.pop();
cur->val += pre;
pre = cur->val;
cur = cur->left; // 左
}
}
}
public:
TreeNode* convertBST(TreeNode* root) {
pre = 0;
traversal(root);
return root;
}
};
Morris 遍历
思路及算法
有一种巧妙的方法可以在线性时间内,只占用常数空间来实现中序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被称为 Morris 遍历。
Morris 遍历的核心思想是利用树的大量空闲指针,实现空间开销的极限缩减。其反序中序遍历规则总结如下:
如果当前节点的右子节点为空,处理当前节点,并遍历当前节点的左子节点;
如果当前节点的右子节点不为空,找到当前节点右子树的最左节点(该节点为当前节点中序遍历的前驱节点);
如果最左节点的左指针为空,将最左节点的左指针指向当前节点,遍历当前节点的右子节点;
如果最左节点的左指针不为空,将最左节点的左指针重新置为空(恢复树的原状),处理当前节点,并将当前节点置为其左节点;
重复步骤 1 和步骤 2,直到遍历结束。
这样我们利用 Morris 遍历的方法,反序中序遍历该二叉搜索树,即可实现线性时间与常数空间的遍历。
代码
C++
class Solution {
public:
TreeNode* getSuccessor(TreeNode* node) {
TreeNode* succ = node->right;
while (succ->left != nullptr && succ->left != node) {
succ = succ->left;
}
return succ;
}
TreeNode* convertBST(TreeNode* root) {
int sum = 0;
TreeNode* node = root;
while (node != nullptr) {
if (node->right == nullptr) {
sum += node->val;
node->val = sum;
node = node->left;
} else {
TreeNode* succ = getSuccessor(node);
if (succ->left == nullptr) {
succ->left = node;
node = node->right;
} else {
succ->left = nullptr;
sum += node->val;
node->val = sum;
node = node->left;
}
}
}
return root;
}
};
·· TreeNode* convertBST(TreeNode* root) {
int sum = 0;
TreeNode* node = root;
二叉树:总结篇!(需要掌握的二叉树技能都在这里了)
力扣二叉树大总结!
不知不觉二叉树已经和我们度过了三十三天,「代码随想录」 **(opens new window)** 里已经发了三十三篇二叉树的文章,详细讲解了30+二叉树经典题目,一直坚持下来的录友们一定会二叉树有深刻理解了。
在每一道二叉树的题目中,我都使用了递归三部曲来分析题目,相信大家以后看到二叉树,看到递归,都会想:返回值、参数是什么?终止条件是什么?单层逻辑是什么?
而且几乎每一道题目我都给出对应的迭代法,可以用来进一步提高自己。
下面Carl把分析过的题目分门别类,可以帮助新录友循序渐进学习二叉树,也方便老录友面试前快速复习,看到一个标题,就回想一下对应的解题思路,这样很快就可以系统性的复习一遍二叉树了。
公众号的发文顺序,就是循序渐进的,所以如下分类基本就是按照文章发文顺序来的,我再做一个系统性的分类。
#二叉树的理论基础
- 关于二叉树,你该了解这些! **(opens new window)** :二叉树的种类、存储方式、遍历方式、定义方式
#二叉树的遍历方式
-
深度优先遍历
- 二叉树:前中后序递归法 **(opens new window)** :递归三部曲初次亮相
- 二叉树:前中后序迭代法(一) **(opens new window)** :通过栈模拟递归
- 二叉树:前中后序迭代法(二)统一风格(opens new window)
-
广度优先遍历
- 二叉树的层序遍历 **(opens new window)** :通过队列模拟
#求二叉树的属性
-
二叉树:是否对称(opens new window)
- 递归:后序,比较的是根节点的左子树与右子树是不是相互翻转
- 迭代:使用队列/栈将两个节点顺序放入容器中进行比较
-
二叉树:求最大深度(opens new window)
- 递归:后序,求根节点最大高度就是最大深度,通过递归函数的返回值做计算树的高度
- 迭代:层序遍历
-
二叉树:求最小深度(opens new window)
- 递归:后序,求根节点最小高度就是最小深度,注意最小深度的定义
- 迭代:层序遍历
-
二叉树:求有多少个节点(opens new window)
- 递归:后序,通过递归函数的返回值计算节点数量
- 迭代:层序遍历
-
二叉树:是否平衡(opens new window)
- 递归:后序,注意后序求高度和前序求深度,递归过程判断高度差
- 迭代:效率很低,不推荐
-
二叉树:找所有路径(opens new window)
- 递归:前序,方便让父节点指向子节点,涉及回溯处理根节点到叶子的所有路径
- 迭代:一个栈模拟递归,一个栈来存放对应的遍历路径
-
二叉树:递归中如何隐藏着回溯(opens new window)
- 详解二叉树:找所有路径 **(opens new window)** 中递归如何隐藏着回溯
-
二叉树:求左叶子之和(opens new window)
- 递归:后序,必须三层约束条件,才能判断是否是左叶子。
- 迭代:直接模拟后序遍历
-
二叉树:求左下角的值(opens new window)
- 递归:顺序无所谓,优先左孩子搜索,同时找深度最大的叶子节点。
- 迭代:层序遍历找最后一行最左边
-
二叉树:求路径总和(opens new window)
- 递归:顺序无所谓,递归函数返回值为bool类型是为了搜索一条边,没有返回值是搜索整棵树。
- 迭代:栈里元素不仅要记录节点指针,还要记录从头结点到该节点的路径数值总和
#二叉树的修改与构造
-
翻转二叉树(opens new window)
- 递归:前序,交换左右孩子
- 迭代:直接模拟前序遍历
-
构造二叉树(opens new window)
- 递归:前序,重点在于找分割点,分左右区间构造
- 迭代:比较复杂,意义不大
-
构造最大的二叉树(opens new window)
- 递归:前序,分割点为数组最大值,分左右区间构造
- 迭代:比较复杂,意义不大
-
合并两个二叉树(opens new window)
- 递归:前序,同时操作两个树的节点,注意合并的规则
- 迭代:使用队列,类似层序遍历
#求二叉搜索树的属性
-
二叉搜索树中的搜索(opens new window)
- 递归:二叉搜索树的递归是有方向的
- 迭代:因为有方向,所以迭代法很简单
-
是不是二叉搜索树(opens new window)
- 递归:中序,相当于变成了判断一个序列是不是递增的
- 迭代:模拟中序,逻辑相同
-
求二叉搜索树的最小绝对差(opens new window)
- 递归:中序,双指针操作
- 迭代:模拟中序,逻辑相同
-
求二叉搜索树的众数(opens new window)
- 递归:中序,清空结果集的技巧,遍历一遍便可求众数集合
- 二叉搜索树转成累加树(opens new window)
- 递归:中序,双指针操作累加
- 迭代:模拟中序,逻辑相同
#二叉树公共祖先问题
-
二叉树的公共祖先问题(opens new window)
- 递归:后序,回溯,找到左子树出现目标值,右子树节点目标值的节点。
- 迭代:不适合模拟回溯
-
二叉搜索树的公共祖先问题(opens new window)
- 递归:顺序无所谓,如果节点的数值在目标区间就是最近公共祖先
- 迭代:按序遍历
#二叉搜索树的修改与构造
-
二叉搜索树中的插入操作(opens new window)
- 递归:顺序无所谓,通过递归函数返回值添加节点
- 迭代:按序遍历,需要记录插入父节点,这样才能做插入操作
-
二叉搜索树中的删除操作(opens new window)
- 递归:前序,想清楚删除非叶子节点的情况
- 迭代:有序遍历,较复杂
-
修剪二叉搜索树(opens new window)
- 递归:前序,通过递归函数返回值删除节点
- 迭代:有序遍历,较复杂
-
构造二叉搜索树(opens new window)
- 递归:前序,数组中间节点分割
- 迭代:较复杂,通过三个队列来模拟
#阶段总结
大家以上题目都做过了,也一定要看如下阶段小结。
每周小结都会对大家的疑问做统一解答,并且对每周的内容进行拓展和补充,所以一定要看,将细碎知识点一网打尽!
- 本周小结!(二叉树系列一)(opens new window)
- 本周小结!(二叉树系列二)(opens new window)
- 本周小结!(二叉树系列三)(opens new window)
- 本周小结!(二叉树系列四)(opens new window)
#最后总结
在二叉树题目选择什么遍历顺序是不少同学头疼的事情,我们做了这么多二叉树的题目了,Carl给大家大体分分类。
- 涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
- 求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
- 求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
注意在普通二叉树的属性中,我用的是一般为后序,例如单纯求深度就用前序,二叉树:找所有路径 **(opens new window)** 也用了前序,这是为了方便让父节点指向子节点。
所以求普通二叉树的属性还是要具体问题具体分析。
二叉树专题汇聚为一张图:
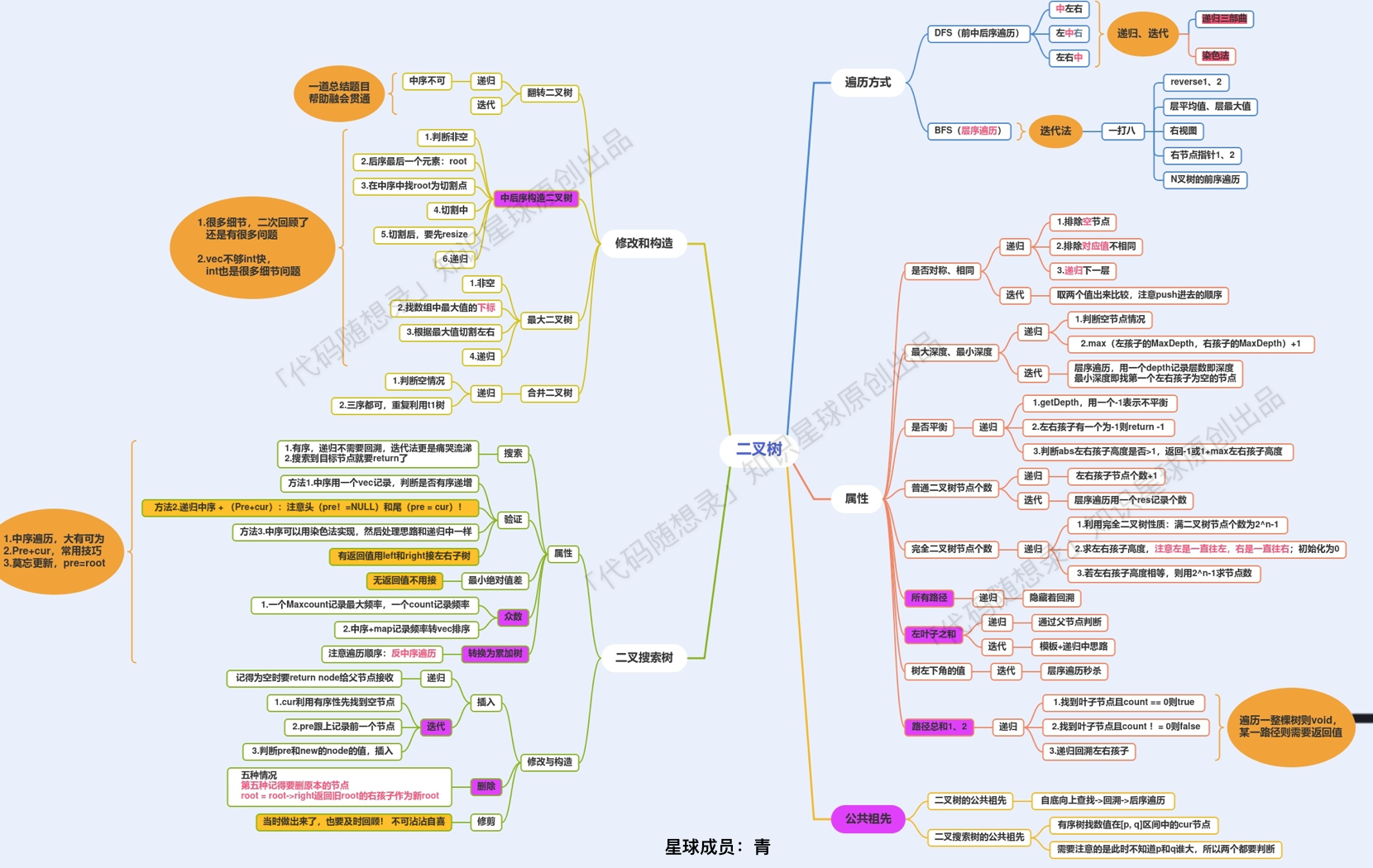
这个图是 代码随想录知识星球 **(opens new window)** 成员:青 **(opens new window)** ,所画,总结的非常好,分享给大家。
最后,二叉树系列就这么完美结束了,估计这应该是最长的系列了,感谢大家33天的坚持与陪伴,接下来我们又要开始新的系列了「回溯算法」!


![BUUCTF靶场[MISC]wireshark、被嗅探的流量、神秘龙卷风、另一个世界](https://img-blog.csdnimg.cn/direct/25715a70b4ee4f5d86a2660a4d1c27ee.png)