ABC352 编程笔记
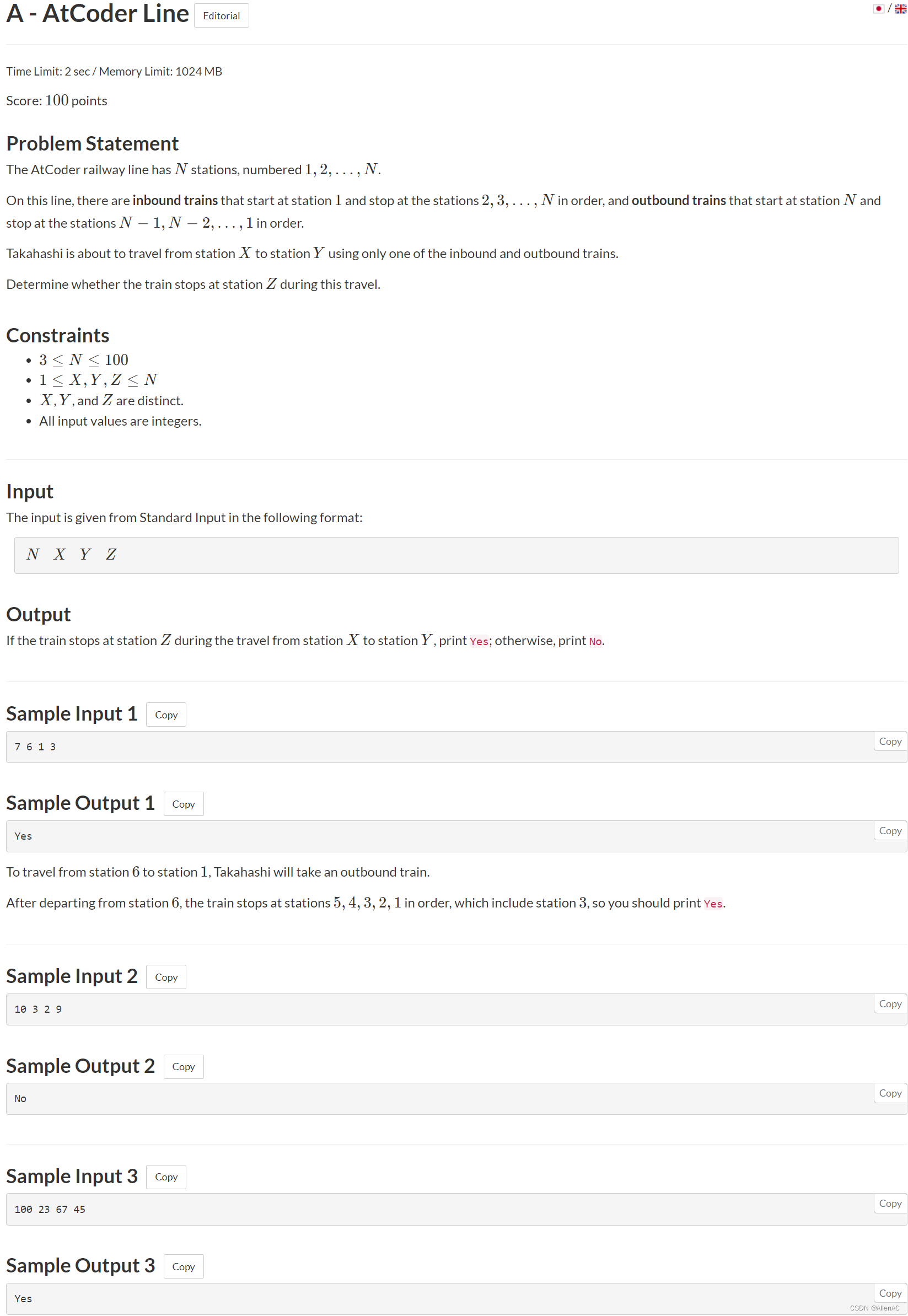
题意:输入,四个数
a
,
b
,
c
,
d
a,b,c,d
a,b,c,d,若
d
d
d 在
c
,
d
c,d
c,d 之间,则输出 Yes,否则输出 No。
正解:直接判断。
#include <bits/stdc++.h>
//#define int long long
using namespace std;
void solve()
{
int a,b,c,d;
cin >> a >> b >> c >> d;
if (d >= b && d <= c || d >= c && d <= b) cout << "Yes";
else cout << "No";
}
signed main()
{
int TTT;
// cin >> TTT;
TTT = 1;
while (TTT--) solve();
return 0;
}
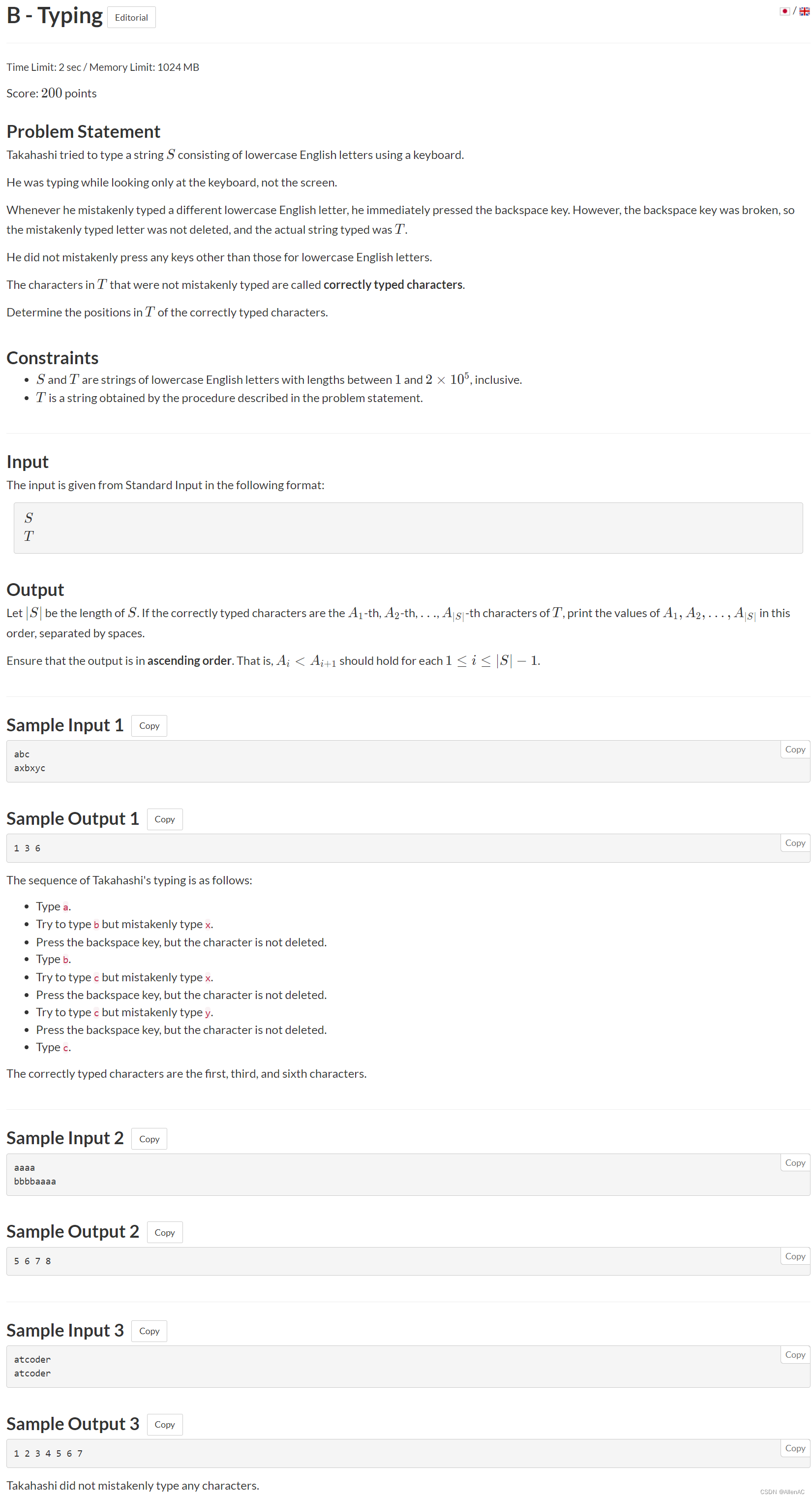
题意:有两个字符串
S
,
T
S,T
S,T,找出
T
T
T 里所有
S
S
S 的字符的下标,并输出。
正解:模拟。
#include <bits/stdc++.h>
//#define int long long
using namespace std;
void solve()
{
string s,t;
cin >> s >> t;
for (int i = 0,j = 0;i < t.size();i++)
if (s[j] == t[i]) cout << i+1 << ' ',j++;
}
signed main()
{
int TTT;
// cin >> TTT;
TTT = 1;
while (TTT--) solve();
return 0;
}
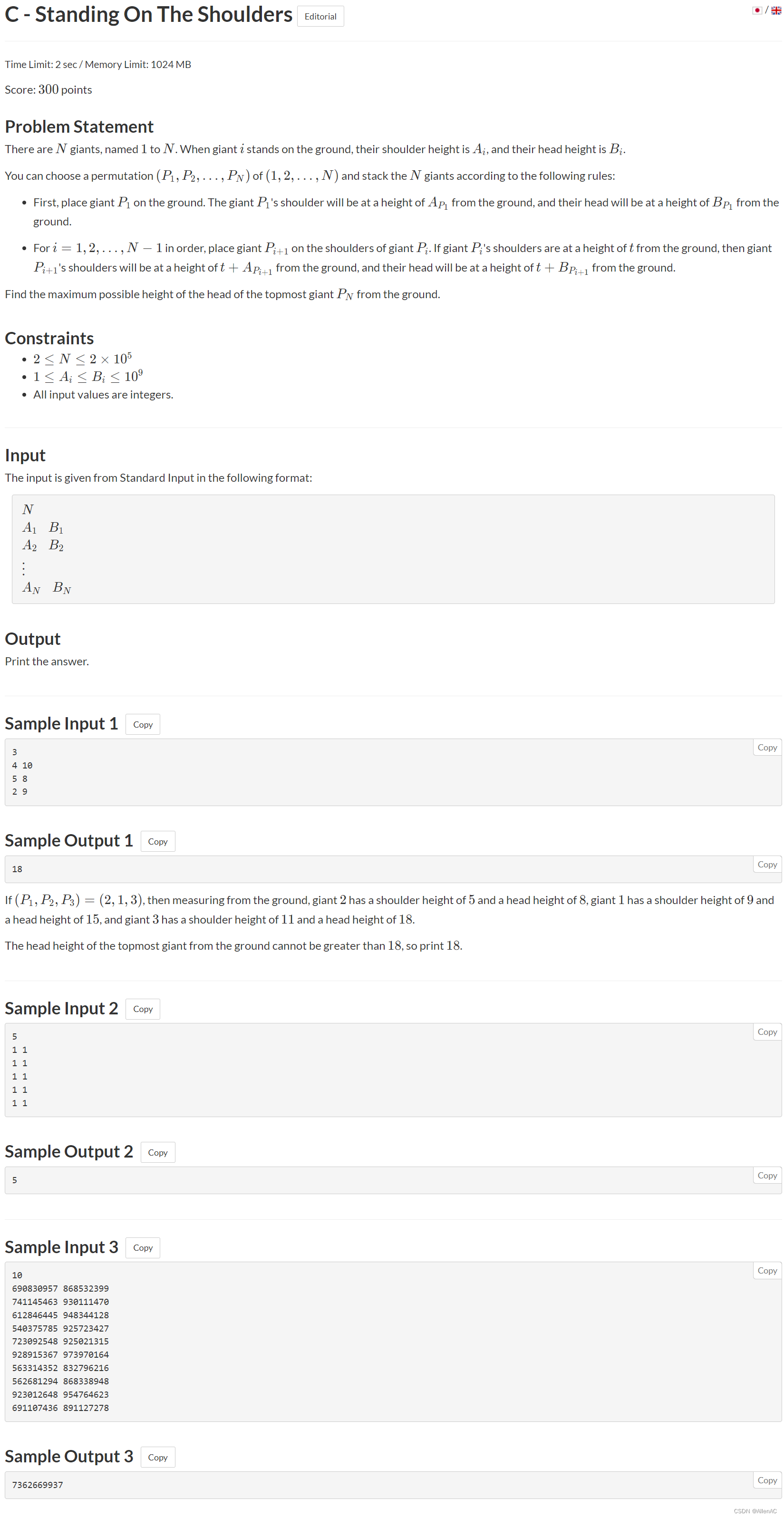
题意:给出所有人的肩膀的海拔高度和头部的海拔高度,求出所有人叠高高后的最高海拔高度。
正解:贪心。
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct node
{
int a,b;
}a[200010];
bool cmp(node a,node b)
{
if (a.a == b.a) return a.b > b.b;
return a.a > b.a;
}
void solve()
{
int n,sum = 0,mx = -1e18;
cin >> n;
for (int i = 1;i <= n;i++) cin >> a[i].a >> a[i].b,sum += a[i].a;
sort(a+1,a+n+1,cmp);
for (int i = 1;i <= n;i++)
{
int now = sum - a[i].a + a[i].b;
mx = max(mx,now);
}
cout << mx;
}
signed main()
{
int TTT;
// cin >> TTT;
TTT = 1;
while (TTT--) solve();
return 0;
}
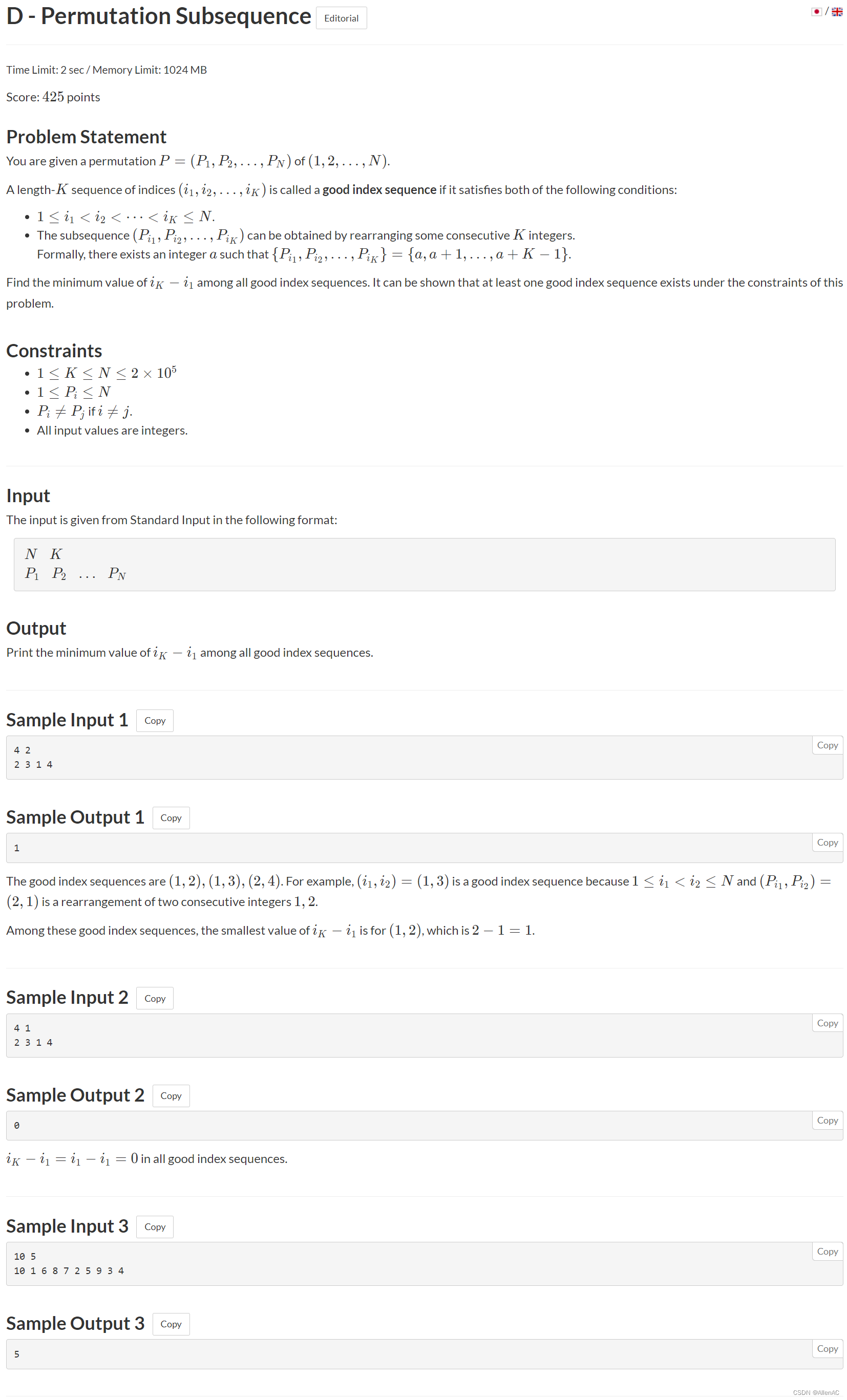
题意:给你一个
1
1
1 到
n
n
n 的排列
p
p
p,找到一个长为
k
k
k 的子序列,满足子序列中元素重排后构成公差为
1
1
1 的等差数列,求子序列的最小跨度。
正解:用 p i p_i pi 表示 i i i 这个数在原数组里的下标,则只需算 min ( p k − p 1 , p k + 1 − p 2 , p k + 2 − p 3 , … , p n − p n − k + 1 ) \min(p_k-p_1,p_{k+1}-p_2,p_{k+2}-p_3,\dots,p_n-p_{n-k+1}) min(pk−p1,pk+1−p2,pk+2−p3,…,pn−pn−k+1),并且让 p a − p a − k + 1 > 0 p_a-p_{a-k+1}>0 pa−pa−k+1>0。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,k;
int a[200010],b[200010];
void solve()
{
cin >> n >> k;
for (int i = 1;i <= n;i++) cin >> a[i],b[a[i]] = i;
set <int> id; //记录选取的数字的下标,自动排序
for (int i = 1;i <= k;i++) id.insert(b[i]);
int ans = *id.rbegin() - *id.begin();
for (int i = k+1;i <= n;i++)
{
id.erase(b[i-k]);
id.insert(b[i]);
ans = min(ans,*id.rbegin() - *id.begin());
}
cout << ans;
}
signed main()
{
int TTT;
// cin >> TTT;
TTT = 1;
while (TTT--) solve();
return 0;
}
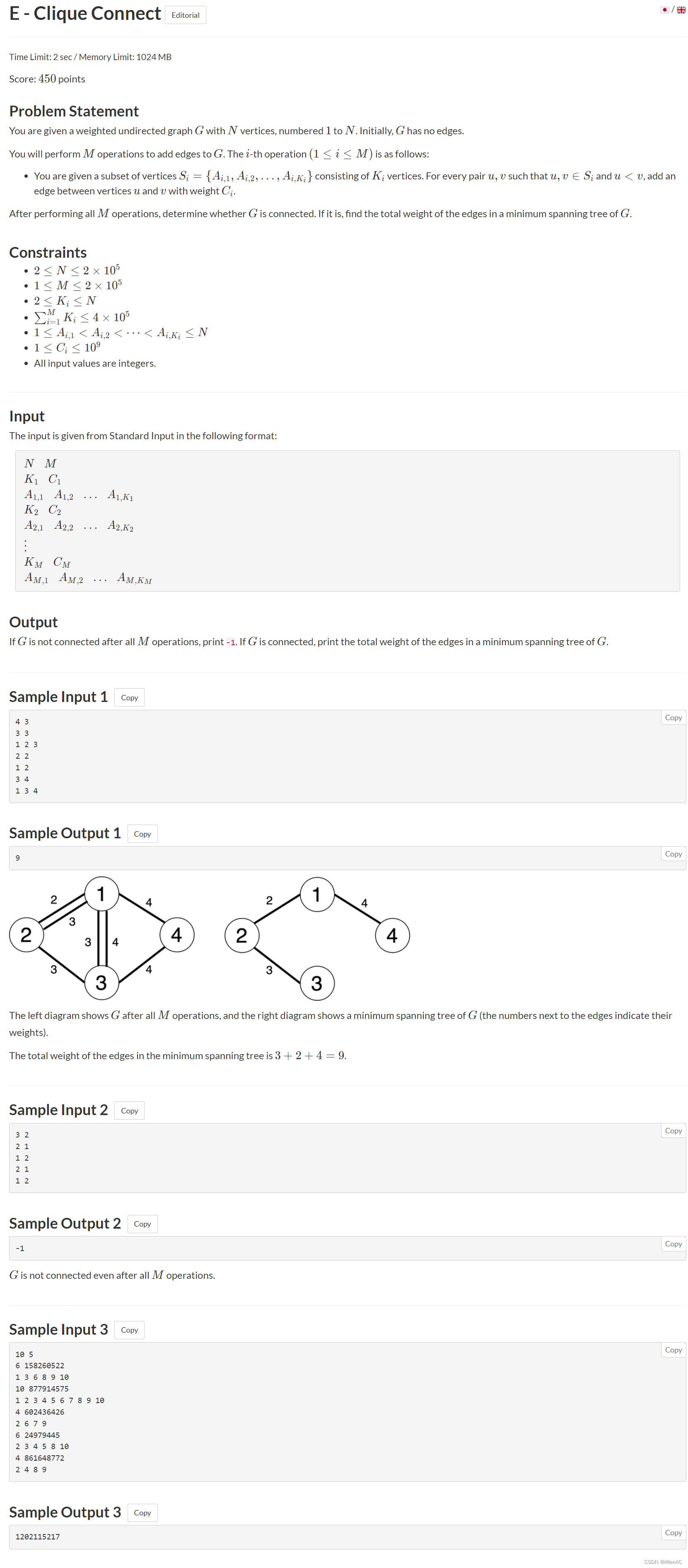
题意:
给你一个加权无向图 G G G,有 N N N 个顶点,编号为 1 1 1 至 N N N。最初, G G G 没有边。
您将执行 M M M 次操作来为 G G G 添加边。第 i i i 次操作 ( 1 ≤ i ≤ M ) (1\le i\le M) (1≤i≤M) 如下:
- 给你一个由 K i K_i Ki 个顶点组成的顶点子集 S i = A i , 1 , A i , 2 , … , A i , K i S_i={A_{i,1}, A_{i,2},\dots,A_{i,K_i}} Si=Ai,1,Ai,2,…,Ai,Ki。对于每一对 u , v u,v u,v,即 u , v ∈ S i u,v∈S_i u,v∈Si 和 u < v u<v u<v,在顶点 u u u 和 v v v 之间添加一条边,权重为 C i C_i Ci。
执行所有 M M M 操作后,确定 G G G 是否相连。如果是,求 G G G 最小生成树中各条边的总重。
正解:
用 Kruskal 的原理:每次添加最小的边。把所有的边权种类从小到大排序后每次添加最小的边。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
pair <int,vector<int> > a[666666];
int fa[666666];
int find(int x) {return x == fa[x] ? x : fa[x] = find(fa[x]);}
int merge(int x,int y)
{
int fx = find(x),fy = find(y);
if (fx == fy) return 0;
fa[fy] = fx;
return 1;
}
bool cmp(pair<int,vector<int> > c,pair<int,vector<int> > b) {return c.first < b.first;}
void solve()
{
cin >> n >> m;
for (int i = 1;i <= n;i++) fa[i] = i;
for (int i = 1;i <= m;i++)
{
int k,c;
cin >> k >> c;
vector <int> v(k);
for (int i = 0;i < k;i++) cin >> v[i];
a[i] = {c,v};
}
sort(a+1,a+m+1,cmp);
int ans = 0;
for (int i = 1;i <= m;i++)
{
int c = a[i].first;
vector <int> v;
for (int j = 0;j < a[i].second.size();j++) v.push_back(a[i].second[j]);
int id = v[0];
for (int j = 0;j < v.size();j++)
if (merge(id,v[j]))
ans += c;
}
for (int i = 1;i <= n;i++)
if (find(1) != find(i))
{
cout << "-1\n";
return ;
}
cout << ans << '\n';
}
signed main()
{
int TTT;
// cin >> TTT;
TTT = 1;
while (TTT--) solve();
return 0;
}