本文简要阐述STK中光照计算的模型。
在航天任务中,通常需要分析地面站、飞行器在一定时间内的光照情况,具体包括:
- 地面站处在光照区和阴影区的具体时间范围;
- 考虑地形遮挡后,地面站的光照区和阴影区的变化情况;
- 飞行器绕地飞行过程中,处于光照区和阴影区的具体时间范围;
- 地面站当地水平系下,太阳方位角、高度角的变化;
- 飞行器轨道器或本体系下,太阳方位角、高度角的变化。
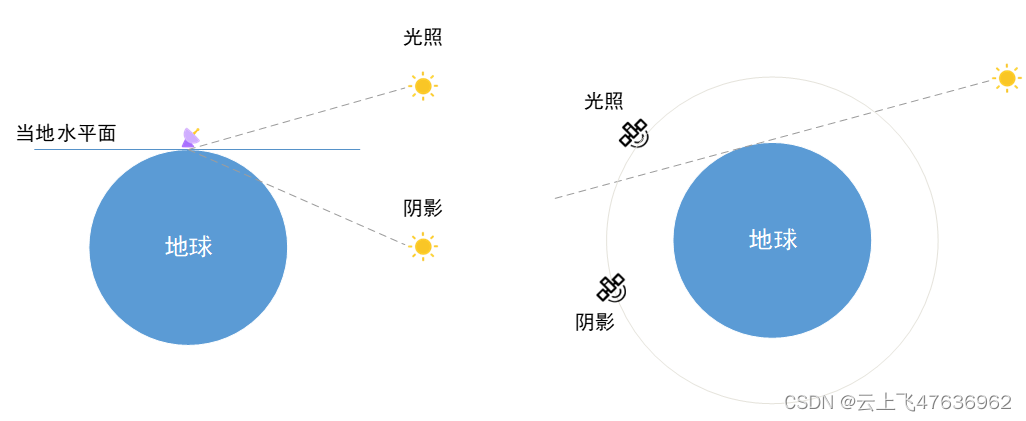
光照计算时,主要考虑的是地球对太阳的遮挡(其它天体也是类似的),见下图所示地面站和飞行器的光照示意图。
对于地面站(左图),考虑地球遮挡,当太阳在当地水平面之上时(对应的太阳的高度角大于0),即地面站为光照状态;反之则为阴影状态。
对于空间飞行器(上面右图),如卫星,当飞行器与太阳连线不被地球遮挡时,则飞行器为光照状态;反之则为阴影状态。
实际计算时,地球形状考虑为椭球体。
下面根据以上所涉及到的光照场景,详细讨论。
坐标系及太阳方位角、高度角
涉及到太阳位置计算时,通常涉及到太阳的方位角和高度角概念,因此首先确定好常用的坐标系和太阳方位角和高度角的定义。
地面站地平坐标系
地面站观测太阳时,采用当地水平坐标系(也称北东地坐标系),简称LH坐标系(Local Horizontal),其定义如下:
- X轴指向当地北方向;
- Y轴指向当地东方向;
- Z轴指向当地天底方向。
XY平面为当地水平面,垂直于地球椭球体法线,见下图。

下图给出了地面站LH系下的太阳方位角和高度角。

飞行器VVLH系
飞行器观测太阳时,通常采用轨道坐标系,简称VVLH坐标系(Vehicle Velocity, Local Horizontal),其定义如下:
- X轴约束在惯性系速度方向(由Y叉乘Z得到);
- Y轴指向轨道面负法向;
- Z轴指向地心方向。
下图为飞行器的VVLH坐标系以及太阳方向矢量的高度角和方位角示意图。

太阳方位角和高度角
在地面站地平坐标系或者飞行器VVLH坐标系中,太阳方位角(Azimuth,简称Az)和高度角(Elevation,简称El)的定义如下图。

- 方位角定义为:X轴与太阳方向矢量在XY平面内的投影矢量的夹角,+X轴为零点,向+Y轴方向为正;
- 高度角定义为:太阳方向矢量与XY平面的夹角,-Z轴方向为正。
注意,对于飞行器本体坐标系(Body),则高度角以+Z轴方向为正。
根据以上定义,实际计算时,首先求得某时刻太阳(通常为视太阳)在地面站LH系或飞行器VVLH系的位置,设为
R
s
\textbf{R}_s
Rs:
R
s
=
[
X
s
,
Y
s
,
Z
s
]
T
\textbf{R}_s=\left[X_s,Y_s,Z_s\right]^T
Rs=[Xs,Ys,Zs]T
则太阳方位角Az和高度角El计算如下:
{
A
z
=
t
a
n
2
−
1
(
Y
s
,
X
s
)
E
l
=
s
i
n
−
1
(
−
Z
s
/
R
s
)
\left\{ \begin{aligned} Az=tan2^{-1}(Y_s,X_s) \\ El=sin^{-1}(-Z_s/R_s) \end{aligned} \right.
{Az=tan2−1(Ys,Xs)El=sin−1(−Zs/Rs)
光照计算模型
无论是地面站还是飞行器,在精确计算光照和阴影的时间时,必须考虑到以下因素:
- 太阳圆盘的大小,以及被遮挡的部分大小;
- 对于地面站,当地水平面附近地形遮挡的影响;
- 对于空间飞行器,考虑地球的遮挡。
同时,太阳的光照状态分为以下三种情形:
- 光照:太阳圆盘完全不被遮挡,地面站或飞行器处于完全光照状态,太阳光照强度因子为1;
- 半影:太阳圆盘部分被遮挡,地面站或飞行器处于半影状态,太阳光照强度因为0-1之间的小数;
- 全影:太阳圆盘完全被遮挡,地面站或飞行器处于完全阴影状态,太阳光照强度因子为0。
首先给出地面站的光照计算模型,见下图。
某时刻,以观测点为中心,视太阳方向的地形最大仰角为 α t \alpha_t αt,视太阳中心(即太阳位置)方向与地形最大仰角方向的夹角为 α g \alpha_g αg,太阳圆盘视半径为 α s \alpha_s αs。
不考虑地形时( α t = 0 \alpha_t=0 αt=0), α g \alpha_g αg即为视太阳方向与当地水平面的夹角,即太阳仰角El。
太阳圆盘视半径
α
s
\alpha_s
αs由下式给出:
α
s
=
s
i
n
−
1
R
o
R
s
\alpha_s=sin^{-1}{\frac{R_o}{R_s}}
αs=sin−1RsRo
上式中,
R
o
R_o
Ro为太阳圆盘半径,取值为695700km,对应的视半径约为0.27°,具体数值与太阳的距离变化而稍有不同。

下图为飞行器的光照计算模型示意图。与地面站不同的是,不需要考虑地形的遮挡,转而考虑地球的遮挡。
某时刻,以观测点为中心,地心方向与地球边缘方向的夹角(称为地球视半径)为
α
t
\alpha_t
αt,视太阳中心(即太阳位置)方向与地球边缘方向的夹角为
α
g
\alpha_g
αg,太阳圆盘视半径为
α
s
\alpha_s
αs。观测点到地球的距离向量为
R
E
\textbf{R}_E
RE。

地球视半径
α
t
\alpha_t
αt可由下式给出:
α
t
=
s
i
n
−
1
R
e
R
E
\alpha_t=sin^{-1}{\frac{R_e}{R_E}}
αt=sin−1RERe
上式中,
R
e
R_e
Re为地球赤道半径,常取6378.14km。
根据上述两种光照模型,太阳光照状态的判别依据如下:
{
光照
:
α
g
>
α
s
阴影
:
α
g
<
−
α
s
半影
:
−
α
s
≤
α
g
≤
α
s
\left\{ \begin{aligned} 光照: & \alpha_g>\alpha_s \\ 阴影: & \alpha_g<-\alpha_s \\ 半影: & -\alpha_s \leq \alpha_g\leq\alpha_s \end{aligned} \right.
⎩
⎨
⎧光照:阴影:半影:αg>αsαg<−αs−αs≤αg≤αs