二分查找二
- 1.山脉数组的峰顶索引
- 2.寻找峰值
- 3.寻找旋转排序数组中的最小值
- 4.点名

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.山脉数组的峰顶索引
题目链接:852. 山脉数组的峰顶索引
题目描述:

题目描述的有些复杂,换成图形就是一个山峰让你找最顶点
算法原理:
首先我们会想到遍历,找到这个数组中第一次出现当前这个值比下一个值大的下标,
解法一:暴力枚举 O(N)
题目要求O(logn),我们看看有没有优化的地方。我们发现这个峰顶值把数组分成了两部分,这时你会想到什么 二段性
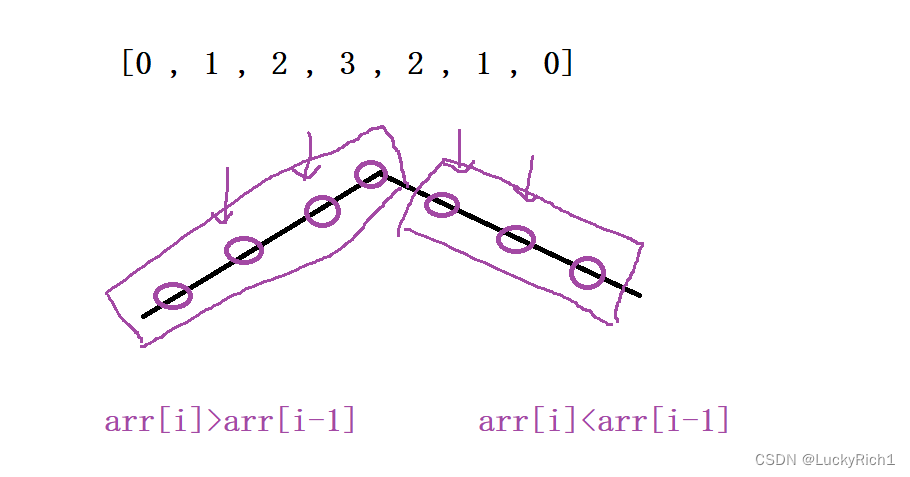
解法二:二分查找算法
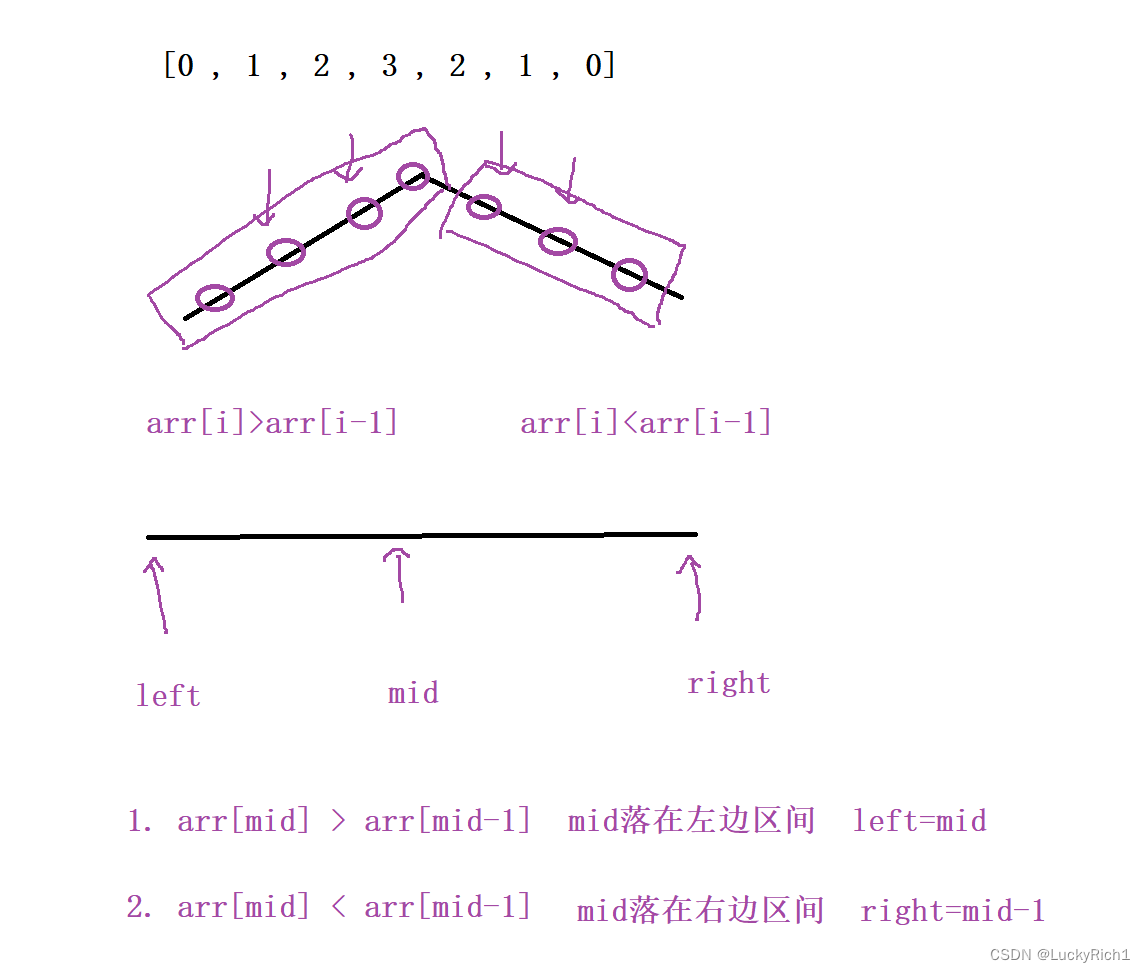
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left=1,right=arr.size()-2;//第一个位置,最后一个位置绝对不可能是
while(left<right)
{
int mid=left+(right-left+1)/2;
if(arr[mid]>arr[mid-1]) left=mid;
else right=mid-1;
}
return left;
}
};
2.寻找峰值
题目链接:162. 寻找峰值
题目描述:

这道题也是找峰值但是和上面不一样的是上面那道题数组就是上下一种情况,而这里数组可能会有三种情况:
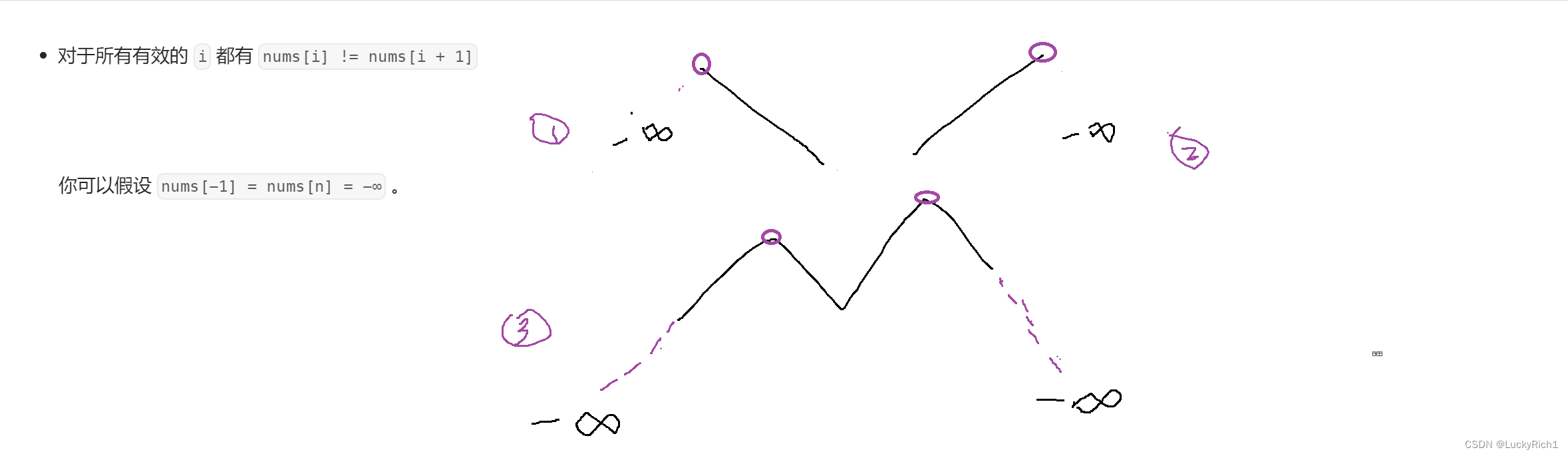
算法原理:
解法一:暴力求解 O(N)
从第一个位置开始,一直往后走,分情况讨论即可
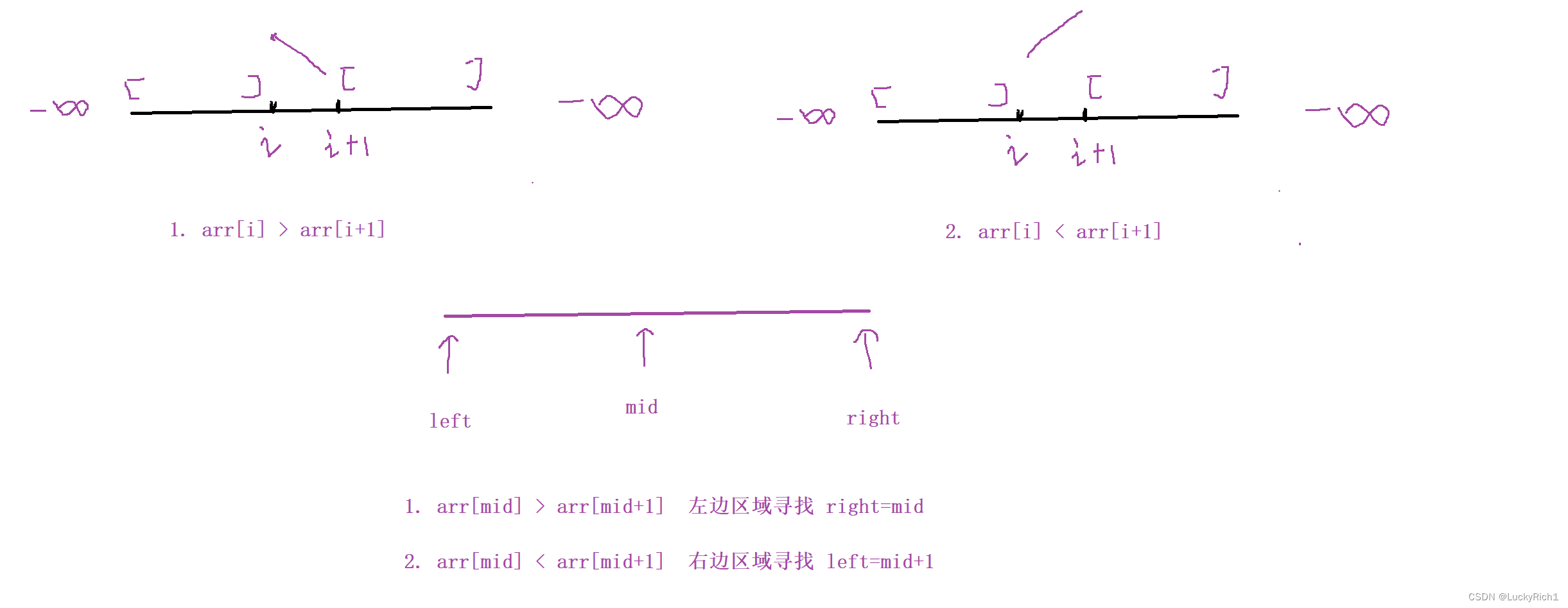
分析一下有没有优化的地方。因为我们就是比较当前位置和下一个位置的关系,所以我们把这个数组抽象出来。
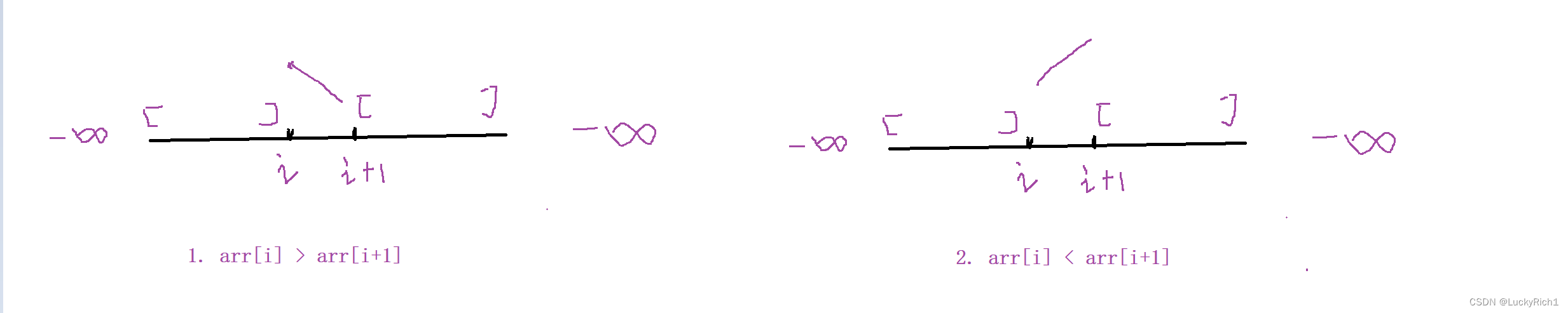
- arr[i] > arr[i+1] ,此时是一个下降趋势,左边区间一定会存在一个峰值,左右都是负无穷,左边是从负无穷开始的,呈现上升趋势然后才下降,所以左边一定是有峰值的。但是右边区间不一定,因为右边是负无穷可能一直下降。接下来去左边寻找。
- arr[i] < arr[i+1],此时是一个上升趋势,左边是从服务器开始可能一直在上升,那可能是没有最终结果的。但是右边一定是有最终结果的,因为右边是负无穷,会降到负无穷的。接下来去右边寻找。
我们发现这两个点的关系把整个数组分成了两部分。然后我们去一个部分去搜索结果。
解法二:二分查找
这道题是严格无序的,因为可能存在一升一降、一升一降。但是我们找到了二段性,因此也可以用二分查找算法。
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left=0,right=nums.size()-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]>nums[mid+1]) right=mid;
else left=mid+1;
}
return left;
}
};
3.寻找旋转排序数组中的最小值
题目链接:153. 寻找旋转排序数组中的最小值
题目描述:

注意题目给的是 互不相同 的元素

算法原理:
这道题暴力求解很容易想到办法,从前往后遍历然后找最小值就可以了
解法一:暴力求解 O(N)
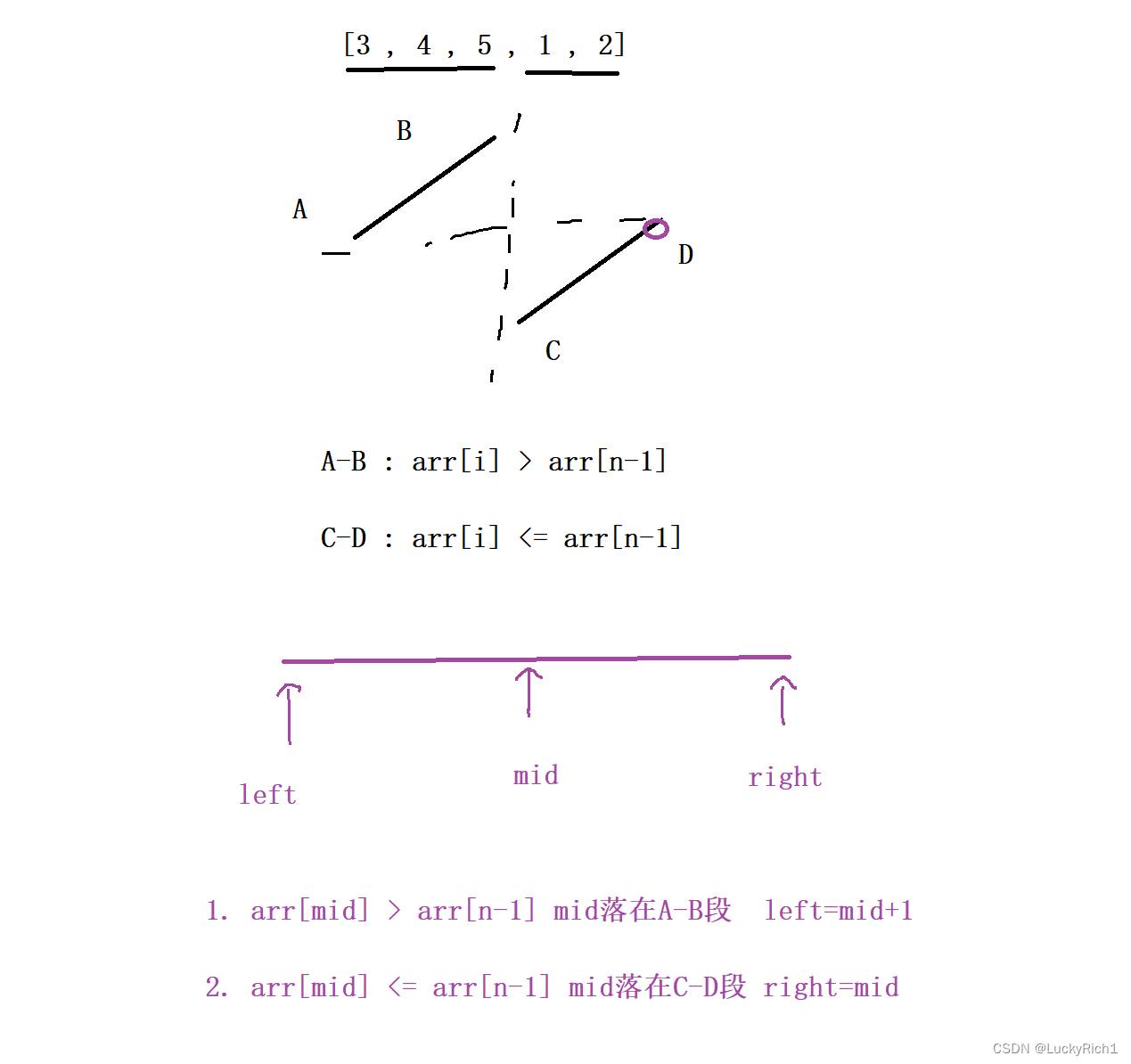
但是我们观察之后,发现这个数组可以分成两段。A-B 递增 C-D也是递增。
假设我们已D为分割点,我们发现A-B内的值大于D,C-D内的值小于等于D。由此我们发现了二段性
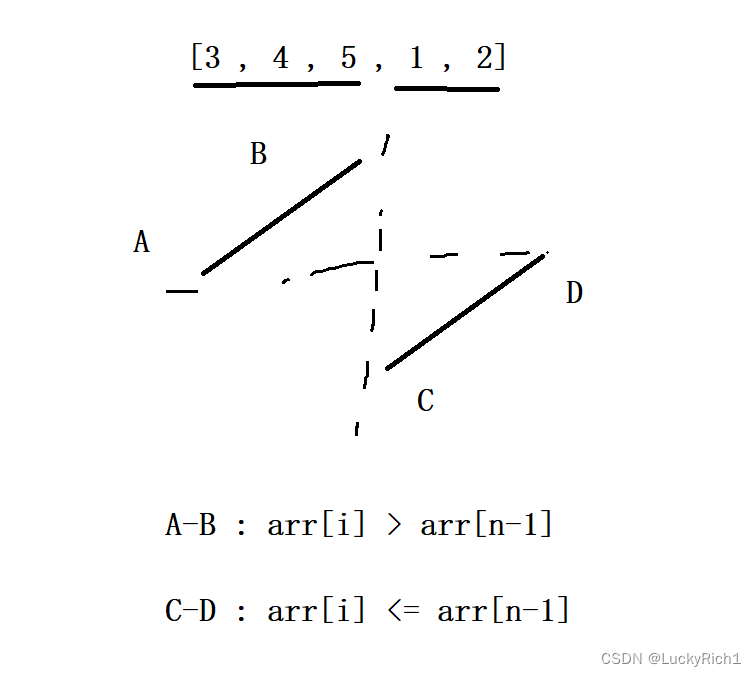
解法二:二分查找算法
class Solution {
public:
int findMin(vector<int>& nums) {
int left=0,right=nums.size()-1;
int n=right;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid] > nums[n]) left=mid+1;
else right=mid;
}
return nums[left];
}
};
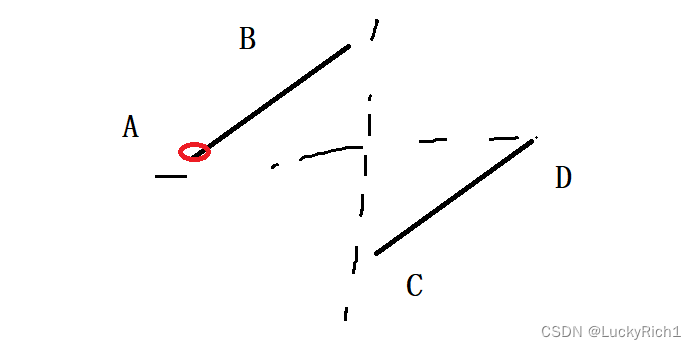
上面我们以D为分割点,那以A点为分割点可不可以?其实也是可以的,但是要注意可以旋转之后是一个严格递增的数组,这里要特别处理一下。以D为分割点不会碰到这个问题。可以自己分析一波
class Solution {
public:
int findMin(vector<int>& nums) {
int left=0,right=nums.size()-1;
int n=right;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]>=nums[0]) left=mid+1;
else right=mid;
}
//旋转后严格单调递增
if(nums[left]>nums[0]) return nums[0];
return nums[left];
}
};
4.点名
题目链接:LCR 173. 点名
题目描述:
算法原理:
这道题很简单,总要考察的是对于一种题你有几个解题思路
解法一:哈希表 时间O(N) 空间O(N)
把数组中所有数映射进hash表
class Solution {
public:
int takeAttendance(vector<int>& records) {
//1.哈希表
int n=records.size()+1;
int hash[10001]={0};
for(int i=0;i<records.size();++i)
{
hash[records[i]]++;
}
for(int i=0;i<n;++i)
{
if(hash[i]==0) return i;
}
}
};
解法二:暴力遍历 O(N)
class Solution {
public:
int takeAttendance(vector<int>& records) {
//2.暴力遍历
int n=0;
for(int i=0;i<records.size();i++)
{
if(records[i] != n) break;
++n;
}
return n;
}
};
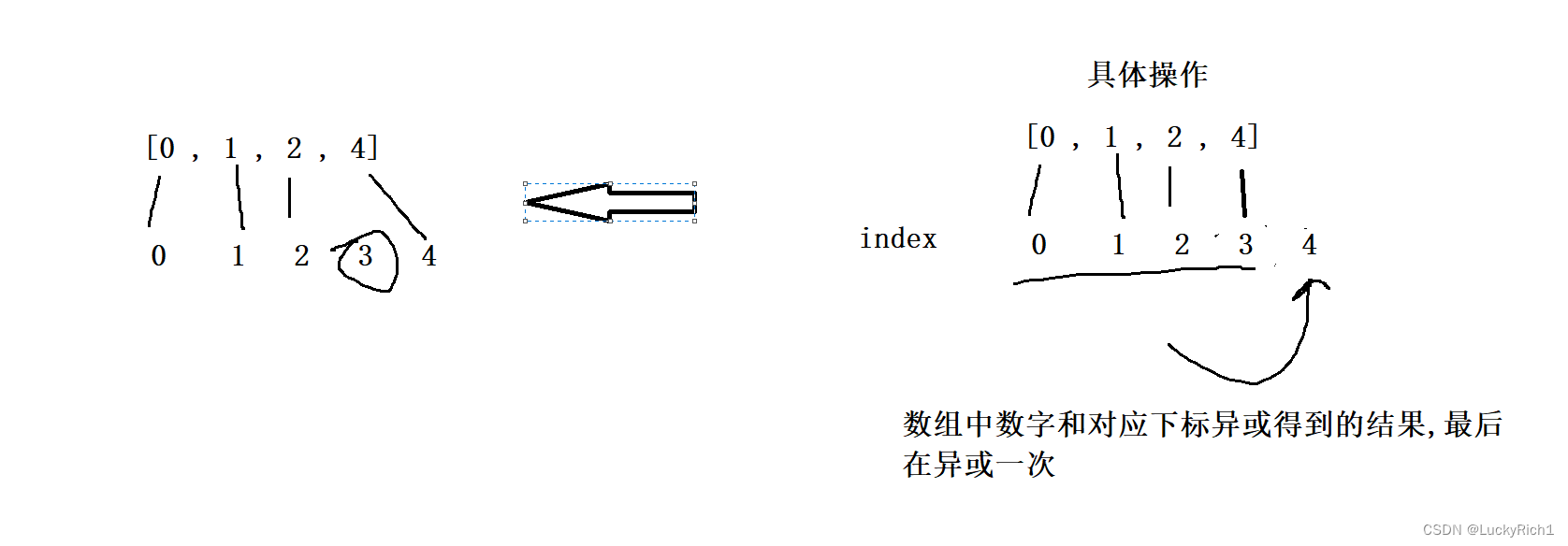
解法三:位运算
将缺少的上面和不缺少的下面进行异或运算。异或运算相同为0,相异为1。最终会有正确结果。具体操作是将数字和下标异或,最后在异或一次就可以了
class Solution {
public:
int takeAttendance(vector<int>& records) {
//3.位运算
int x = 0;
for (int i = 0; i < records.size(); i++)
x ^= records[i] ^ i ;
return x^records.size();
}
};
解法四:等差数列求和
class Solution {
public:
int takeAttendance(vector<int>& records) {
//4.求和公式
int n = records.size();
int sum = (1+n)*n/2;
for(int i = 0;i<records.size();++i)
{
sum-=records[i];
}
return sum;
}
};
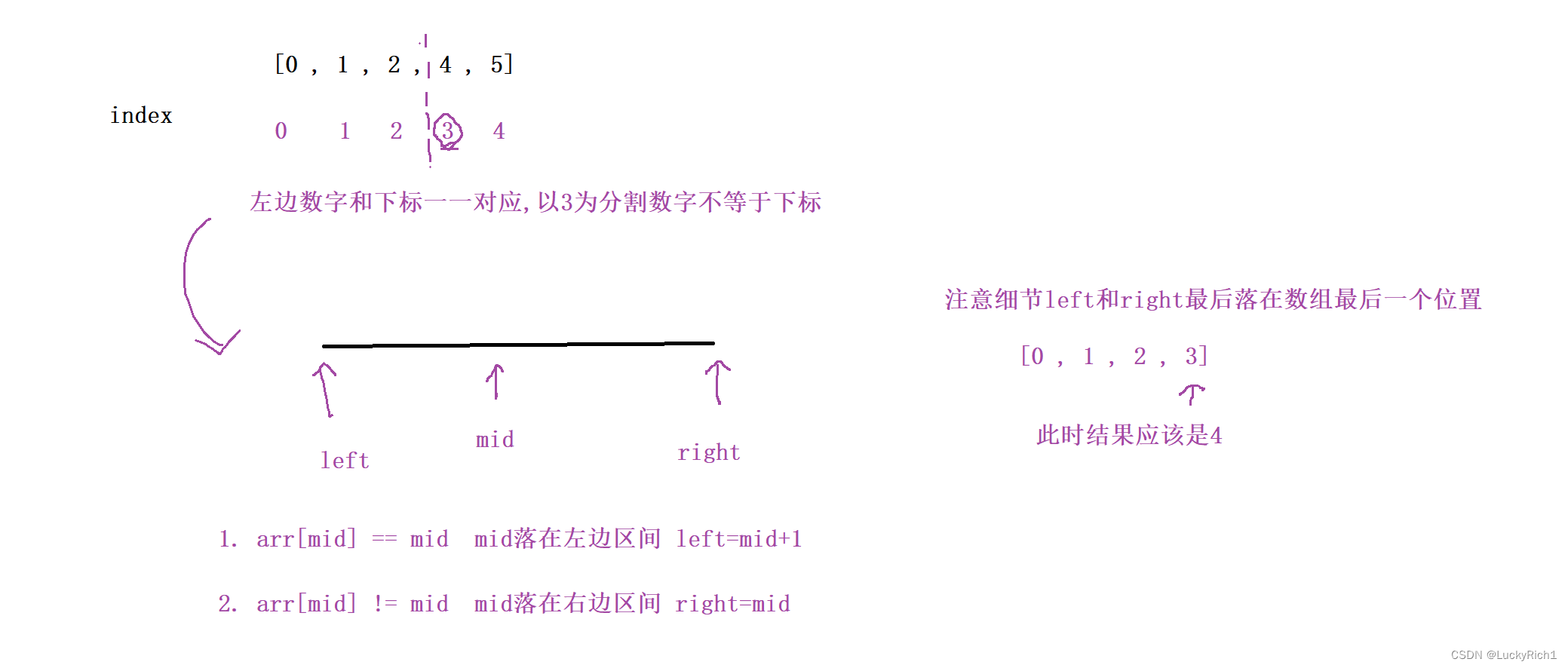
上面时间复杂度都是O(N),思考一下看看有没有优化的可能

由此发现二段性
解法五:二分查找算法
class Solution {
public:
int takeAttendance(vector<int>& records) {
//0.二分查找
int left=0,right=records.size()-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(records[mid]==mid) left=mid+1;
else right=mid;
}
if(left == records[left]) return left+1;
else return left;
}
};