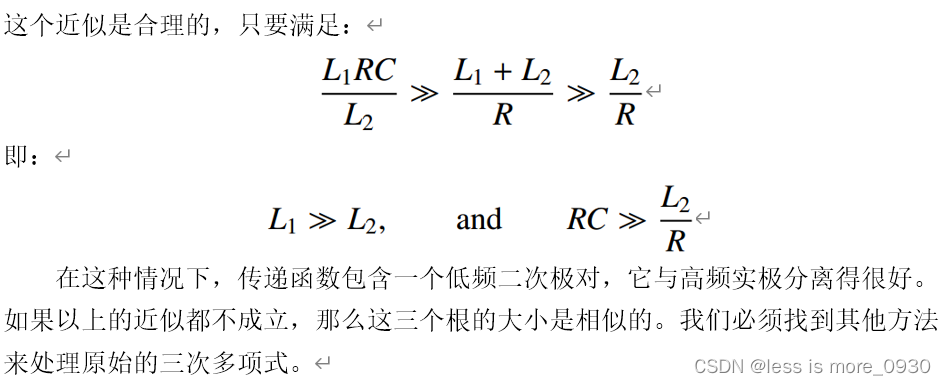
一、动力学方程
机器人的动力学公式描述如下:

式中,
τ
\boldsymbol{\tau}
τ表示关节驱动力矩矢量;
q
,
q
˙
,
q
¨
\boldsymbol{q} ,\; \dot{\boldsymbol { q }} ,\; \ddot{\boldsymbol { q }}
q,q˙,q¨分别为广义的关节位置、速度和加速度;
M
\boldsymbol{M}
M为关节的空间惯量矩阵;
C
\boldsymbol{C}
C为科氏力和离心力耦合矩阵;
G
\boldsymbol{G}
G为重力;
F
f
\boldsymbol{F}_f
Ff为关节摩擦力。
机器人的动力学参数包括惯性参数和摩擦参数。
(1)惯性参数有:连杆质量
m
m
m、相对于连杆坐标系的质心矢量
r
\boldsymbol{r}
r和转动惯量矩阵
I
\boldsymbol{I}
I。其中,质心矢量
r
\boldsymbol{r}
r可以表示为:

式中,
r
x
r_x
rx、
r
y
r_y
ry和
r
z
r_z
rz分别表示质心矢量
r
\boldsymbol{r}
r在连杆坐标系下三个坐标轴的分量。转动惯量矩阵
I
\boldsymbol{I}
I为包含六个独立元素的二维矩阵,表示为:

式中,主对角元素为惯性矩,非主对角元素为惯性积。
(2)机器人动力学建模中常用的摩擦模型为库伦-粘滞摩擦模型,其表达式为:

式中,
f
c
f_c
fc和
f
v
f_v
fv分别表示库伦摩擦系数和粘滞摩擦系数;
v
v
v表示关节速度。注意:对于库伦摩擦系数的处理不同人有不同的处理,有的地方认为库伦摩擦是对称的,即当机器人关节正向旋转和反向旋转时,库伦摩擦力大小相等,方向相反,也即
f
c
+
=
f
c
−
f_c^+ = f_c^-
fc+=fc−;也有的地方认为库伦摩擦是非对称的,即当机器人关节正向旋转和反向旋转时,库伦摩擦力大小不相等。
二、机器人工具箱描述动力学方程
2.1 动力学参数赋值
在机器人工具箱中,提供了如下动力学参数输入接口:
(1)Link.m:表示连杆的质量;
(2)Link.r:表示连杆的质心矢量;
(3)Link.I:表示连杆的惯量矩阵;
(4)Link.Jm:表示驱动电机的转动惯量;
(5)Link.B:表示粘滞摩擦系数;
(6)Link.Tc:表示库伦摩擦系数;
(7)Link.G:表示电机齿轮传动比(默认为1)
这里仍然以3-DOF平面机械臂为例:
%% 动力学
% RRR机械臂
clear;
close all;
clc;
% theta(z) d(z) a(x) alpha(x)
RRR_L(1) = Link([ 0 0 1 0 ],'standard');
RRR_L(2) = Link([ 0 0 0.8 0 ],'standard');
RRR_L(3) = Link([ 0 0 0.6 0 ],'standard');
% 连杆1动力学参数
RRR_L(1).m = 4.0;
RRR_L(1).r = [0.12; 0.08; 0.31];
RRR_L(1).I = [0.32 0.01 0.02;
0.01 0.12 0.11;
0.02 0.11 0.41];
RRR_L(1).Jm = 0.0012;
RRR_L(1).B = 0.00148;
RRR_L(1).Tc = [+0.395, -0.435];
RRR_L(1).G = 1.2;
% 连杆2动力学参数
RRR_L(2).m = 15.2;
RRR_L(2).r = [-0.475; 0.097; 0.06];
RRR_L(2).I = [1.21 0.21 0.32;
0.21 0.52 0.11;
0.32 0.11 0.51];
RRR_L(2).Jm = 0.0048;
RRR_L(2).B = 0.00329;
RRR_L(2).Tc = [+0.462; -0.561];
RRR_L(2).G = 1.4;
% 连杆3动力学参数
RRR_L(3).m = 0.6;
RRR_L(3).r = [0.01; 0.097; 0.016];
RRR_L(3).I = [0.021 0.03 0.382;
0.03 0.152 0.11;
0.382 0.11 0.651];
RRR_L(3).Jm = 0.0061;
RRR_L(3).B = 0.00429;
RRR_L(3).Tc = [+0.262; -0.661];
RRR_L(3).G = 1.7;
three_link = SerialLink(RRR_L, 'name', '3-DOF');
采用dyn( )函数可以查看动力学参数,如图所示:



2.2 动力学方程中的各项表示
(1)空间惯量矩阵
M
(
q
)
\boldsymbol{M}(\boldsymbol{q})
M(q)
机器人的空间惯量是机器人各关节的位姿的函数,在不同机器人位形时具有不同的值。机器人工具箱中可以调用robot.inertia(q)函数获得空间惯量矩阵。
例如:当3-DOF平面机械臂三个关节角度为30°、45°和60°时,其空间惯量矩阵为:

(2)科氏力和离心力耦合矩阵
C
(
q
,
q
˙
)
\boldsymbol{C}(\boldsymbol{q},\dot{\boldsymbol{q}})
C(q,q˙)
科氏力和离心力耦合矩阵是关节位置和速度的函数。机器人工具箱中可以调用robot.coriolis(q, qd)函数获得该耦合矩阵。
例如:当3-DOF平面机械臂三个关节角度为30°、45°和60°,三个关节速度为10°/s、20°/s和30°/s时,其科氏力和离心力耦合矩阵为:

(3)重力矩阵
G
(
q
)
\boldsymbol{G}(\boldsymbol{q})
G(q)
重力矩阵与机器人的位形有关,是对各关节所受重力的描述,其值不受机器人的运动的影响。机器人工具箱中可以调用robot.gravload(q, grav)函数来获得重力矩阵,其中grav自定义重力加速度向量。
例如:当3-DOF平面机械臂三个关节角度为30°、45°和60°,重力加速度向量为
y
y
y轴负向,即grav = [0; -9.8; 0]。重力矩阵为:

(4)摩擦力矩阵
F
f
(
q
˙
)
\boldsymbol{F}_f(\dot{\boldsymbol{q}})
Ff(q˙)
摩擦力矩阵是由各关节的给定摩擦参数数值决定的,大小与各关节的速度有关。机器人工具箱中可以调用robot.friction(qd)函数来获得重力矩阵。
例如:当3-DOF平面机械臂三个关节速度为10°/s、20°/s和30°/s时,其摩擦力矩阵为:

三、逆动力学分析
机器人的逆动力学分析是在给定机器人关节位置、速度和加速度时,计算得到机器人各关节所需要的力和力矩大小。机器人工具箱中可以调用robot.rne(q, qd, qdd, grav)函数来计算逆动力学。其中,q, qd, qdd分别表示机器人关节位置、速度和加速度;grav表示自定义的重力加速度矢量。除此之外,还可以添加参数fext,表示末端执行器受到的外力和力矩
[
F
x
,
F
y
,
F
z
,
τ
x
,
τ
y
,
τ
z
]
[F_x,\: F_y,\: F_z,\: \tau_x,\: \tau_y,\: \tau_z]
[Fx,Fy,Fz,τx,τy,τz]
例子:让3-DOF平面机械臂按照下图所示的轨迹运动。

代码:
%% 动力学
% RRR机械臂
clear;
close all;
clc;
% theta(z) d(z) a(x) alpha(x)
RRR_L(1) = Link([ 0 0 1 0 ],'standard');
RRR_L(2) = Link([ 0 0 0.8 0 ],'standard');
RRR_L(3) = Link([ 0 0 0.6 0 ],'standard');
% 连杆1动力学参数
RRR_L(1).m = 4.0;
RRR_L(1).r = [0.12; 0.08; 0.31];
RRR_L(1).I = [0.32 0.01 0.02;
0.01 0.12 0.11;
0.02 0.11 0.41];
RRR_L(1).Jm = 0.0012;
RRR_L(1).B = 0.00148;
RRR_L(1).Tc = [+0.395, -0.435];
RRR_L(1).G = 1.2;
% 连杆2动力学参数
RRR_L(2).m = 15.2;
RRR_L(2).r = [-0.475; 0.097; 0.06];
RRR_L(2).I = [1.21 0.21 0.32;
0.21 0.52 0.11;
0.32 0.11 0.51];
RRR_L(2).Jm = 0.0048;
RRR_L(2).B = 0.00329;
RRR_L(2).Tc = [+0.462; -0.561];
RRR_L(2).G = 1.4;
% 连杆3动力学参数
RRR_L(3).m = 5.6;
RRR_L(3).r = [0.01; 0.097; 0.016];
RRR_L(3).I = [0.921 0.03 0.382;
0.03 0.252 0.11;
0.382 0.11 1.251];
RRR_L(3).Jm = 0.0061;
RRR_L(3).B = 0.00429;
RRR_L(3).Tc = [+0.262; -0.661];
RRR_L(3).G = 1.7;
three_link = SerialLink(RRR_L, 'name', '3-DOF');
delta_t = 0.02;
t = 0:delta_t:4;
m = length(t);
theta1 = 60*sin(4*pi*t/4);
theta2 = 60*sin(2*pi*t/4);
theta3 = 30*sin(2*pi*t/4);
theta1_d = 60*pi*cos(4*pi*t/4);
theta2_d = 30*pi*cos(2*pi*t/4);
theta3_d = 15*pi*cos(2*pi*t/4);
theta1_dd = -60*pi*pi*sin(4*pi*t/4);
theta2_dd = -15*pi*pi*sin(2*pi*t/4);
theta3_dd = -7.5*pi*pi*sin(2*pi*t/4);
q = [theta1;theta2;theta3]'*pi/180;
qd = [theta1_d;theta2_d;theta3_d]'*pi/180;
qdd = [theta1_dd;theta2_dd;theta3_dd]'*pi/180;
% 关节位置、速度、加速度绘图
figure(1)
subplot(3,1,1)
plot(t, q(:,1)*180/pi, 'b')
hold on
plot(t, q(:,2)*180/pi, 'r--')
hold on
plot(t, q(:,3)*180/pi, 'm')
xlabel('time (s)', 'Interpreter', 'latex')
ylabel('$\theta$ (deg)', 'Interpreter', 'latex')
legend('$\theta_1$','$\theta_2$','$\theta_3$', 'Interpreter', 'latex')
set(gca, 'FontName','Times New Roman')
subplot(3,1,2)
plot(t, qd(:,1)*180/pi, 'b')
hold on
plot(t, qd(:,2)*180/pi, 'r--')
hold on
plot(t, qd(:,3)*180/pi, 'm')
xlabel('time (s)', 'Interpreter', 'latex')
ylabel('$\dot{\theta}$ (deg)', 'Interpreter', 'latex')
legend('$\dot{\theta_1}$','$\dot{\theta_2}$','$\dot{\theta_3}$', 'Interpreter', 'latex')
set(gca, 'FontName','Times New Roman')
subplot(3,1,3)
plot(t, qdd(:,1)*180/pi, 'b')
hold on
plot(t, qdd(:,2)*180/pi, 'r--')
hold on
plot(t, qdd(:,3)*180/pi, 'm')
xlabel('time (s)', 'Interpreter', 'latex')
ylabel('$\ddot{\theta}$ (deg)', 'Interpreter', 'latex')
legend('$\ddot{\theta_1}$','$\ddot{\theta_2}$','$\ddot{\theta_3}$', 'Interpreter', 'latex')
set(gca, 'FontName','Times New Roman')
set(gcf, 'color',[1 1 1]);
% 运动示意
figure(2)
three_link.plot(q,'trail','b');
% 逆动力学
grav = [0; -9.8; 0];
tau = three_link.rne(q, qd, qdd, grav);
% 关节驱动力矩
figure(3)
plot(t,tau(:,1), 'b')
hold on
plot(t, tau(:,2), 'r--')
hold on
plot(t, tau(:,3), 'm')
xlabel('time (s)', 'Interpreter', 'latex')
ylabel('$\tau$ (N/m)', 'Interpreter', 'latex')
legend('$\tau_1$','$\tau_2$','$\tau_3$', 'Interpreter', 'latex')
set(gca, 'FontName','Times New Roman')
set(gcf, 'color',[1 1 1]);
运行结果:


四、结语
机器人工具箱还有其他的一些应用,譬如正动力学分析、视觉相关应用等,不过笔者对这些没有接触过,就不误导大家了。
我是木头人,以上全是个人见解,有问题请大家评论区指出,大家共同进步!!