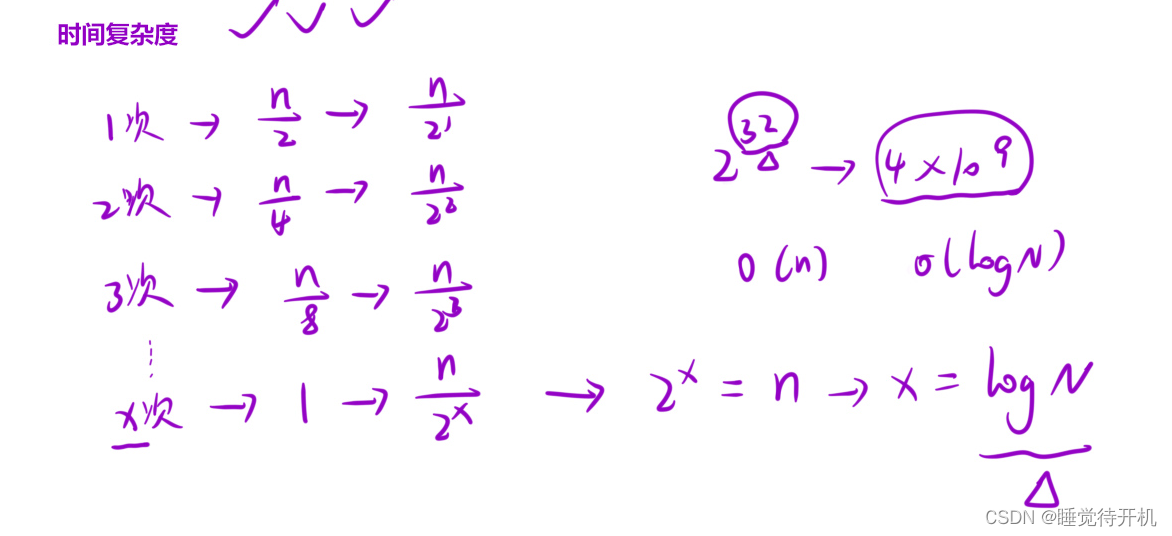本节博客详述“二分查找”并且以例子来进行讨论,有需要借鉴即可。
目录
- 1.二分查找
- 1.1使用前提
- 1.2模板
- 2.题目
- 3.题解代码示例
- 4.二分查找的一般模板
- 5.总结
1.二分查找
1.1使用前提
使用的条件:数组具有“二段性”,二段性指的是数组可以根据某一规律分为两组,且在干掉一半之后仍可以对另一半进行复用相同的规律。
1.2模板
二分查找的代码具有高度统一性,因而可以套用模板,但这并不意味着自己不需要用脑子无脑套模板。
一般二分查找模板、查找左边界二分模板、查找右边界二分模板。
下面是通过一道具体的题目来介绍二分查找算法的由来。
2.题目
题目链接:LINK

首先肯定是暴力解法,挨个遍历就行了,找到了返回对应的下标,找不到返回-1
但是这个暴力解法有点慢,慢就慢在一次只能干掉一个数字。
有序数组满足“二段性”,这里的“二段性”就是以某个数字作比较,可以将数组分为比这个数字大的一组和小的一组,因而可以利用有序的特点直接上二分查找算法。
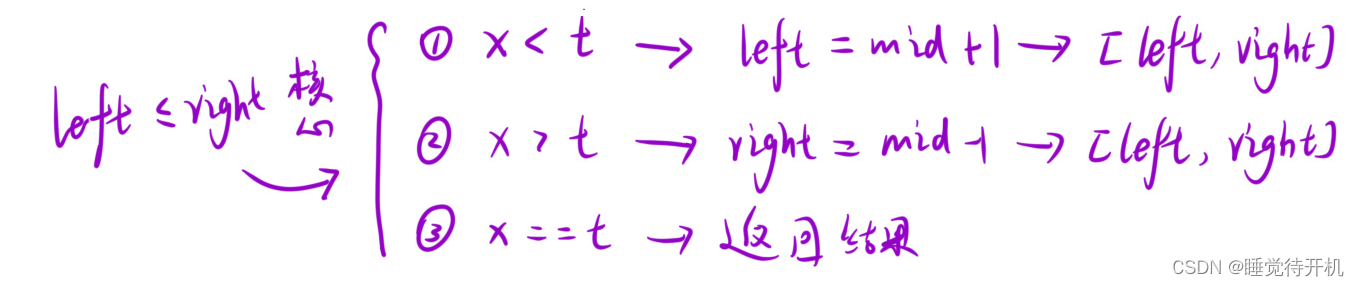
思考:结束条件是什么?
答:left <= right,这个等于一定要注意,因为一个数字也要判断一下。
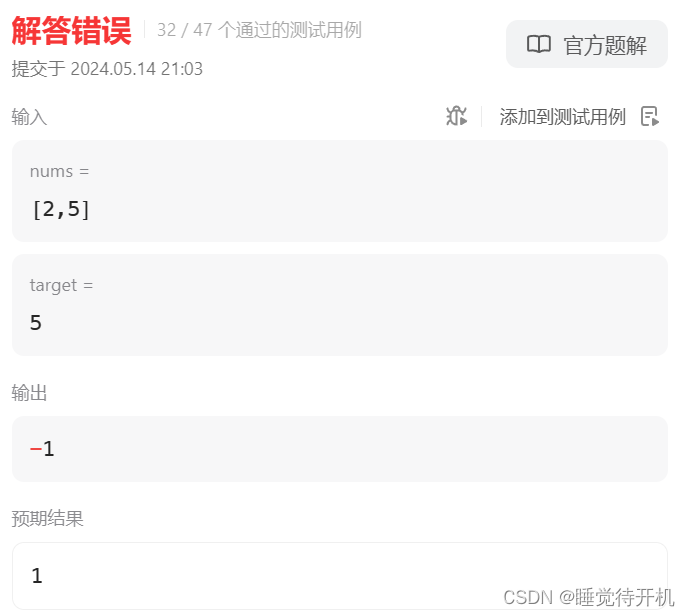
不然会出下以下“悲剧”:
思考:为什么一定得二分,而不是三分、四分…N分?
答:这里推一篇文章,有兴趣可以看一下:LINK
二分查找复杂度
答:logN
3.题解代码示例
class Solution {
public:
int search(vector<int>& nums, int target)
{
//一般情况
for(int left = 0,right = nums.size() - 1,mid; left <= right;)
{
//mid = (left + right) / 2;
mid = left + (right - left) / 2;//优化,防止两数相加溢出问题
if(nums[mid] > target)right = mid - 1;
else if(nums[mid] < target)left = left + 1;
else return mid;
}
return -1;
}
};
4.二分查找的一般模板
while(left < right)
{
int mid = left + (right - left) / 2;
if(...)
//
else if(...)
//
else
return ...
}
5.总结
我感觉二分查找大部分人是比较熟悉的,这里需要注意两个点,为什么是二分?二分查找的使用前提一定是有序吗?
题目太简单,不多说。
EOF