1.均值
定义:均值是一组数据中所有数值的总和除以数据的数量。均值是数据的中心趋势的一种度量,通常用符号 xˉ 表示。
:对于包含 n 个数据的数据集 {𝑥1,𝑥2,...,𝑥𝑛},均值 xˉ 计算公式为:


2.期望
定义:期望是随机变量所有可能值的加权平均值,其中权重是每个值出现的概率。
随机变量*概率密度函数,分为离散型和连续型;


3.方差和标准差
定义:
方差衡量数据的离散程度,表示数据与均值的平方差的平均值。(每个数据与均值相减,为了消除负数的影响,在平方,最后求和取平均,就得到了方差)
标准差是方差的平方根,表示数据的离散程度的实际量度(标准差是方差求平方根,方差需要平方去消除负号的影响,同时单位也随之改变,通过开根号,得到数据的离散程度的实际度量)。


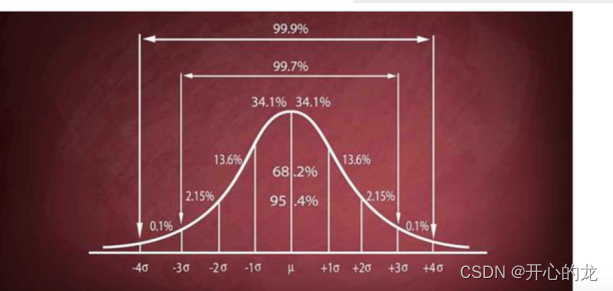
4.正态分布
定义:正态分布是一种连续概率分布,呈钟形曲线,完全由均值和标准差决定。

其中函数关于均值对称,在均值取最大值,求导得最大值;
x轴是渐近线,从负无穷到一个方差是饱函数,中间部分是凸函数

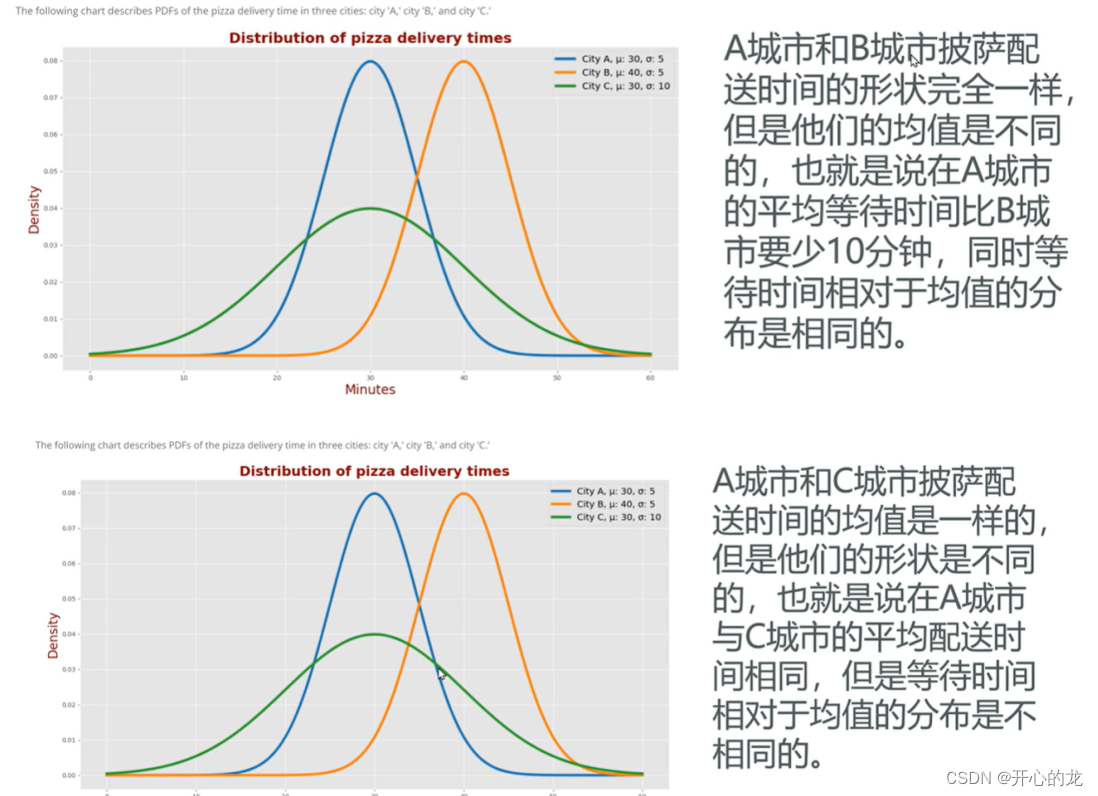
以三个城市A,B,C披萨的配送时间为例,其中A和B成是正态分布形状完全一样,但是它们的均值不同,意味着A成是要比B成是平均等待时间要少十分钟;
而A和C均值相同,但是他们的形状不同 ,意味着平均配送时间是相同的,但是等待时间相对于均值的分布是不同的;

5.估计
定义:估计是利用样本数据来推测总体参数值的过程。
常用于估算系统不可见状态,每一测量和计算的参数都是一个估计值
常见估计方法:
- 点估计:使用一个样本统计量作为总体参数的估计值,例如样本均值作为总体均值的估计。
- 区间估计:给出一个区间范围,使得总体参数落在该区间内的概率较高。

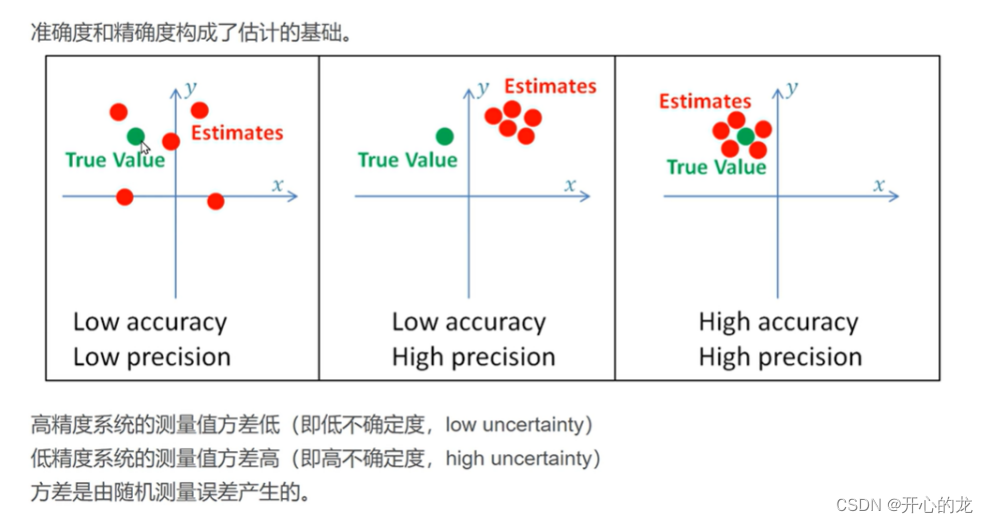
6.准确度
定义:准确度是指测量结果与真实值之间的接近程度。
计算公式:常用绝对误差或相对误差来衡量。
例子:如果实际值为100,测量值为98,准确度可以通过绝对误差 ∣100−98∣=2 来衡量。
7.精确度(Precision)
定义:精确度是指多次测量结果之间的一致性。
计算公式:常用标准差或方差来衡量。
例子:若多次测量结果为 {98,99,100,101,102},则精确度较高。


8.随机变量
定义:随机变量是指取值由随机试验结果决定的变量。
类型:
- 离散型随机变量:取值为有限或可数多个,例如掷骰子的结果。
- 连续型随机变量:取值为连续区间,例如人的身高。
例子:掷骰子的结果 X 是一个离散型随机变量,其可能取值为 {1,2,3,4,5,6}{1,2,3,4,5,6}。

8.1期望:
8.1.1一维随机变量
8.1.2二维随机变量
8.2方差标准差
8.2.1一维随机变量的方差和标准差
首先求出随机变量的数学期望,然后用随机变量减去数学期望,平方求和,再求数学期望,就是随机变量的方差;