UVa11419 SAM I AM
- 题目链接
- 题意
- 分析
- AC 代码
题目链接
UVA - 11419 SAM I AM
题意
给出一个 R×C 大小的网格,网格上面放了一些目标。可以在网格外发射子弹,子弹会沿着垂直或者水平方向飞行,并且打掉飞行路径上的所有目标,如下图所示。你的任务是计算出最少需要多少子弹,各从哪些位置发射,才能把所有目标全部打掉。
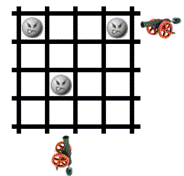
分析
求二分图最大匹配,可得第一部分答案:最小覆盖数。
说一下求覆盖点方案的思路:首先可知,从所有匹配点中选出一半作为覆盖点即可,未匹配点不选作覆盖点(当然,不是说未匹配点一定不能作为覆盖点,而是在求出一个最大匹配后,从所有匹配点中选一半作为覆盖点一定是可行解)。从未匹配点u入手,如果u连有边(u,v),说明v一定是覆盖点,那么对于和v相连的其他边(v,w),w不是覆盖点,然后需要继续这样对点w分析,这是一个dfs拓展匈牙利树的过程。
总结一下:从所有X点集的未匹配点出发做dfs扩展匈牙利树,标记树中的所有点,则X中的未标记点和Y中的已标记点组成了所求的最小覆盖点集。
AC 代码
#include <iostream>
#include <cstring>
using namespace std;
#define N 1005
int g[N][N], c[N], dx[N], dy[N], px[N], py[N], vis[N], q[N], m, nx, ny, clk, d, INF = N<<1; bool f[N];
bool search() {
memset(dx, -1, sizeof(dx)); memset(dy, -1, sizeof(dy)); d = INF;
int head = 0, tail = 0;
for (int i=1; i<=nx; ++i) if (px[i] < 0) q[tail++] = i, dx[i] = 0;
while (head < tail) {
int u = q[head++];
if (dx[u] > d) break;
for (int i=0, v; i<c[u]; ++i) if (dy[v = g[u][i]] < 0) {
dy[v] = dx[u] + 1;
py[v] < 0 ? d = dy[v] : (dx[py[v]] = dy[v] + 1, q[tail++] = py[v]);
}
}
return d != INF;
}
bool dfs(int u) {
for (int i=0, v; i<c[u]; ++i) if (vis[v = g[u][i]] != clk && dy[v] == dx[u]+1) {
vis[v] = clk;
if (py[v] >= 0 && dy[v] == d) continue;
if (py[v] < 0 || dfs(py[v])) {
px[u] = v; py[v] = u;
return true;
}
}
return false;
}
int max_match() {
memset(px, -1, sizeof(px)); memset(py, -1, sizeof(py)); memset(vis, -1, sizeof(vis));
int cc = clk = 0;
while (search()) {
++clk;
for (int i=1; i<=nx; ++i) if (px[i] < 0 && dfs(i)) ++cc;
}
return cc;
}
void dfs2(int u) {
f[u] = 1;
for (int i=0, v; i<c[u]; ++i) if (!vis[v = g[u][i]]) {
vis[v] = 1;
if (!f[py[v]]) dfs2(py[v]);
}
}
void solve() {
memset(c, 0, sizeof(c));
while (m--) {
int u, v; cin >> u >> v; g[u][c[u]++] = v;
}
cout << max_match();
memset(f, 0, sizeof(f)); memset(vis, 0, sizeof(vis));
for (int i=1; i<=nx; ++i) if (px[i] < 0) dfs2(i);
for (int i=1; i<=nx; ++i) if (!f[i]) cout << " r" << i;
for (int i=1; i<=ny; ++i) if (vis[i]) cout << " c" << i;
cout << endl;
}
int main() {
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
while (cin >> nx >> ny >> m && (nx || ny || m)) solve();
return 0;
}